Исследование динамических рядов социально-экономических явлений, определения закономерности их развития во времени создают основу для статистического прогнозирования (экстраполяции) и интерполяции изучаемого явления.
Экстраполяция в динамике предполагает распространение полученных выводов, полученных в прошлом на будущее время. При этом предполагается, что закономерность развития, динамического ряда сохраняется в будущем.
Самый простой метод экстраполяции это применение средних характеристик ряда динамики: среднего абсолютного прироста и среднего темпа роста.
Более часто применяют экстраполяцию динамического ряда по аналитически выровненным рядам.
После того как по фактическому динамическому ряду выявлен тренд (выровненный ряд, отражающий тенденцию развития) экстраполяцию можно провести двумя методами:
1. графический метод. Заключается в построении точного графика выровненного динамического ряда, на котором линию полученного тренда продлевают до интересующей нас даты.
2. аналитический метод. При данном методе в рассчитанное аналитическое уравнение подставляют номер интересующего нас периода.
Выявление основной тенденции развития дает возможность определять также значение недостающего члена ряда – интерполяция. Также проводится графическим и аналитическим методом.
Пример 6.1. По району имеются данные о количестве правонарушений на 10000 человек, за ряд лет 
(табл. 6.1).
Таблица 6.1
| Год | 
| Год |
|
| 1997 | 19 | 2002 | 20 |
| 1998 | 17 | 2003 | 21 |
| 1999 | 18 | 2004 | 16 |
| 2000 | 20 | 2005 | 17 |
| 2001 | 21 | 2006 | 20 |
Рассчитать:
1. Показатели динамики:
· абсолютный прирост (цепной и базисный);
· темп роста (цепной и базисный);
· темп прироста (цепной);
· абсолютное значение 1% прироста;
· средние показатели динамики.
Решение.
1. Рассчитаем показатели динамики, результаты занесем в табл. 6.2.
По полученным результатам рассчитаем средние показатели динамики.
Средний абсолютный прирост рассчитывается как:
.
где 
- количество абсолютных приростов.
Таблица 6.2
| Год | Количество правонарушений. | Абсолютный прирост | Темп прироста | Темп прироста | Абсолютное значение 1% прироста | ||
| цепной | базисный | цепной | базисный | цепной | цепного | ||
| 
| 
| 
| 
| 
| ||
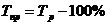
| 1997 | 19 | - | - | - | - | - | - |
| 1998 | 17 | -2 | -2 | 89,47 | 89,47 | -10,53 | 0,19 |
| 1999 | 18 | 1 | -1 | 105,88 | 94,74 | 5,88 | 0,17 |
| 2000 | 20 | 2 | 1 | 111,11 | 105,26 | 11,11 | 0,18 |
| 2001 | 21 | 1 | 2 | 105,00 | 110,53 | 5,00 | 0,20 |
| 2002 | 20 | -1 | 1 | 95,24 | 105,26 | -4,76 | 0,21 |
| 2003 | 21 | 1 | 2 | 105,00 | 110,53 | 5,00 | 0,20 |
| 2004 | 16 | -5 | -3 | 76,19 | 84,21 | -23,81 | 0,21 |
| 2005 | 17 | 1 | -2 | 106,25 | 89,47 | 6,25 | 0,16 |
| 2006 | 20 | 3 | 1 | 117,65 | 105,26 | 17,65 | 0,17 |
Средний коэффициент роста рассчитывается как:
– число коэффициентов роста.
Средний темп роста рассчитывается как:
Средний темп прироста рассчитывается как:
Среднее абсолютное значение 1% среднего прироста рассчитывается как:
Пример 6.2. По району имеются данные о количестве правонарушений на 10000 человек, за ряд лет (табл. 6.3).
Таблица 6.3
| Год | Количество правонарушений.
|
| 1998 | 16 |
| 1999 | 18 |
| 2000 | 20 |
| 2001 | 21 |
| 2002 | 20 |
| 2003 | 21 |
| 2004 | 23 |
| 2005 | 27 |
| 2006 | 20 |
Необходимо:
1. Провести выравнивание динамического ряда.
а) методом средних скользящих;
б) аналитическое выравнивание по линейной функции, и по функции параболы второго порядка.
2. Провести экстраполяцию на 2007 год.
Решение.
1. Проведем выравнивание динамического ряда.
а) Метод средних скользящих. Для выравнивания динамического ряда методом средних скользящих рассчитаем средние уровни за определенное количество лет (в нашем случае возьмем три года) со сдвигом на одну дату.
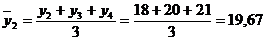
И т.д. результаты занесем в табл. 23.
б) Аналитическое выравнивание динамического ряда по прямой. Линейная функция динамического ряда имеет вид:
Рассчитаем неизвестные параметры уравнения 
и 
при помощи системы уравнений:
Назначим точку отсчета, при которой сумма показателей времени исследуемого динамического ряда будет равна нулю (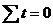
) (табл. 22).
Сократим систему уравнений:
отсюда
и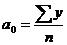 
В таблице 6.4 рассчитаем все необходимые значения для определения параметров уравнения.
Таблица 6.4
| Год |
| Средняя скользящая
| 
| 
| 
| 
|
| 1998 | 16 | -4 | 16 | -64 | 16,465 | |
| 1999 | 18 | 18,00 | -3 | 9 | -54 | 17,682 |
| 2000 | 20 | 19,67 | -2 | 4 | -40 | 18,899 |
| 2001 | 21 | 20,33 | -1 | 1 | -21 | 20,116 |
| 2002 | 20 | 20,67 | 0 | 0 | 0 | 21,333 |
| 2003 | 21 | 21,33 | 1 | 1 | 21 | 22,550 |
| 2004 | 23 | 23,67 | 2 | 4 | 46 | 23,767 |
| 2005 | 27 | 25,33 | 3 | 9 | 81 | 24,984 |
| 2006 | 26 | 4 | 16 | 104 | 26,201 | |
| Итого | 192 | 0 | 60 | 73 |
Рассчитаем:
Подставим полученные значение в уравнение:
Подставляя в полученные уравнения значения рассчитаем теоретические значения :
И т.д. результаты занесем в таблицу 22.
2. Проведем экстраполяцию на 2007 год. Номер t для 2007 г. будет 5. Подставим данные номера в уравнение линейного тренда и проведем прогнозирование на данный период.
Для 2007 г: 
Пример 6.3. По району имеются данные о количестве правонарушений на 10000 человек, за ряд лет (табл. 6.4).
Таблица 6.4
| Год | Количество правонарушений.
|
| 1998 | 7 |
| 1999 | 8 |
| 2000 | 11 |
| 2001 | 10 |
| 2002 | 12 |
| 2003 | 14 |
| 2004 | 10 |
| 2005 | 13 |
| 2006 | 11 |
Провести выравнивание динамического ряда по параболе второго порядка.
Решение.
Аналитическое уравнение параболы второго порядка имеет вид: 
Для расчета параметров уравнения используем систему уравнений:
.
Приравняв 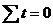система сократится:
Рассчитаем все возможные значения в табл. 6.5
Таблица 6.5
| Год | надой |
|
| 
|
| 
|
|
| 1998 | 7 | -4 | 16 | 256 | -28 | 112 | 6,80 |
| 1999 | 8 | -3 | 9 | 81 | -24 | 72 | 8,60 |
| 2000 | 11 | -2 | 4 | 16 | -22 | 44 | 10,04 |
| 2001 | 10 | -1 | 1 | 1 | -10 | 10 | 11,13 |
| 2002 | 12 | 0 | 0 | 0 | 0 | 0 | 11,86 |
| 2003 | 14 | 1 | 1 | 1 | 14 | 14 | 12,23 |
| 2004 | 10 | 2 | 4 | 16 | 20 | 40 | 12,24 |
| 2005 | 13 | 3 | 9 | 81 | 39 | 117 | 11,90 |
| 2006 | 11 | 4 | 16 | 256 | 44 | 176 | 11,20 |
| Итого | 96 | 0 | 60 | 708 | 33 | 585 |
Из уравнения (5) рассчитаем:
Останется система из двух уравнений:
подставим значения 
Рассчитаем параметр 
, исключив из системы параметр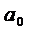 
, для этого:
а) разделим 7-е и 8-е уравнения на коэффициенты, стоящие при 
, т.е. 7-е на 9, а 8-е на 60.
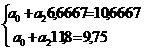
Таким образом, коэффициенты, стоящие при 
, будут равны единице.
б) далее из 8-го сокращенного уравнения вычтем 7-е сокращенное уравнение, исключив таким образом .
Получится уравнение с одним неизвестным 
:
Подставим параметры 
и 
в 1-е уравнение и рассчитаем параметр .
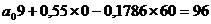
Подставим значение параметров в уравнение 
:
Подставляя значение и рассчитаем значения .
Пример 6.4. За ряд лет по хозяйству имеются данные о сдельной среднемесячной заработной плате (табл. 6.6).
Таблица 6.6
| Месяц | Год | ||
| 2004г | 2005г | 2006г | |
| Январь | 7,28 | 8,52 | 5,46 |
| Февраль | 7,54 | 9,12 | 5,88 |
| Март | 8,06 | 7,80 | 6,93 |
| Апрель | 6,76 | 7,44 | 4,62 |
| Май | 6,50 | 7,20 | 3,78 |
| Июнь | 6,11 | 6,72 | 3,99 |
| Июль | 4,16 | 6,12 | 3,32 |
| Август | 6,50 | 7,68 | 6,72 |
| Сентябрь | 8,19 | 7,80 | 6,72 |
| Октябрь | 8,97 | 7,80 | 7,77 |
| Ноябрь | 9,10 | 8,16 | 8,19 |
| Декабрь | 10,14 | 8,28 | 9,87 |
Необходимо выявить сезонность изменений среднемесячной оплаты труда, предварительно проведя аналитическое выравнивание динамического ряда по прямой или по другой более подходящей функции.
Решение. Проведем выравнивание динамического ряда по прямой 
(табл. 26).
Рассчитаем параметры уравнения (см. пример 6.7).
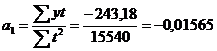
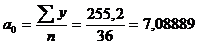
Таблица 6.7
| Месяц | 
|
|
|
|
|
| А | 1 | 2 | 3 | 4 | 5 |
| Январь | 7,28 | -35 | 1225 | -254,80 | 7,63 |
| Февраль | 7,54 | -33 | 1089 | -248,82 | 7,60 |
| Март | 8,06 | -31 | 961 | -249,86 | 7,57 |
| Апрель | 6,76 | -29 | 841 | -196,04 | 7,54 |
| Май | 6,50 | -27 | 729 | -175,50 | 7,51 |
| Июнь | 6,11 | -25 | 625 | -152,75 | 7,48 |
| Июль | 4,16 | -23 | 529 | -95,68 | 7,45 |
| Август | 6,50 | -21 | 441 | -136,50 | 7,42 |
| Сентябрь | 8,19 | -19 | 361 | -155,61 | 7,39 |
| Октябрь | 8,97 | -17 | 289 | -152,49 | 7,35 |
| Ноябрь | 9,10 | -15 | 225 | -136,50 | 7,32 |
| Декабрь | 10,14 | -13 | 169 | -131,82 | 7,29 |
| Январь | 8,52 | -11 | 121 | -93,72 | 7,26 |
| Февраль | 9,12 | -9 | 81 | -82,08 | 7,23 |
| Март | 7,80 | -7 | 49 | -54,60 | 7,20 |
| Апрель | 7,44 | -5 | 25 | -37,20 | 7,17 |
| Май | 7,20 | -3 | 9 | -21,60 | 7,14 |
| Июнь | 6,72 | -1 | 1 | -6,72 | 7,10 |
| Июль | 6,12 | 1 | 1 | 6,12 | 7,07 |
| Август | 7,68 | 3 | 9 | 23,04 | 7,04 |
| Сентябрь | 7,80 | 5 | 25 | 39,00 | 7,01 |
| Октябрь | 7,80 | 7 | 49 | 54,60 | 6,98 |
| Ноябрь | 8,16 | 9 | 81 | 73,44 | 6,95 |
| Декабрь | 8,28 | 11 | 121 | 91,08 | 6,92 |
| Январь | 5,46 | 13 | 169 | 70,98 | 6,89 |
| Февраль | 5,88 | 15 | 225 | 88,20 | 6,85 |
| Март | 6,93 | 17 | 289 | 117,81 | 6,82 |
| Апрель | 4,62 | 19 | 361 | 87,78 | 6,79 |
| Май | 3,78 | 21 | 441 | 79,38 | 6,76 |
| Июнь | 3,99 | 23 | 529 | 91,77 | 6,73 |
| Июль | 3,32 | 25 | 625 | 83,00 | 6,70 |
| Август | 6,72 | 27 | 729 | 181,44 | 6,67 |
| Сентябрь | 6,72 | 29 | 841 | 194,88 | 6,64 |
| Октябрь | 7,77 | 31 | 961 | 240,87 | 6,61 |
| Ноябрь | 8,19 | 33 | 1089 | 270,27 | 6,57 |
| Декабрь | 9,87 | 35 | 1225 | 345,45 | 6,54 |
| Итого | 255,20 | 0 | 15540 | -243,18 |
Подставляя значение в полученное уравнение рассчитаем значения 
.
Рассчитаем индексы сезонности (табл. 6.8):
Таблица 6.8
| Месяц |
| 
| Индексы сезонности
|
| Январь | 7,28 | 7,63 | 0,9535 |
| Февраль | 7,54 | 7,60 | 0,9916 |
| Март | 8,06 | 7,57 | 1,0644 |
| Апрель | 6,76 | 7,54 | 0,8964 |
| Май | 6,50 | 7,51 | 0,8655 |
| Июнь | 6,11 | 7,48 | 0,8170 |
| Июль | 4,16 | 7,45 | 0,5586 |
| Август | 6,50 | 7,42 | 0,8764 |
| Сентябрь | 8,19 | 7,39 | 1,1090 |
| Октябрь | 8,97 | 7,35 | 1,2197 |
| Ноябрь | 9,10 | 7,32 | 1,2427 |
| Декабрь | 10,14 | 7,29 | 1,3906 |
| Январь | 8,52 | 7,26 | 1,1735 |
| Февраль | 9,12 | 7,23 | 1,2615 |
| Март | 7,80 | 7,20 | 1,0836 |
| Апрель | 7,44 | 7,17 | 1,0381 |
| Май | 7,20 | 7,14 | 1,0090 |
| Июнь | 6,72 | 7,10 | 0,9459 |
| Июль | 6,12 | 7,07 | 0,8652 |
| Август | 7,68 | 7,04 | 1,0906 |
| Сентябрь | 7,80 | 7,01 | 1,1126 |
| Октябрь | 7,80 | 6,98 | 1,1175 |
| Ноябрь | 8,16 | 6,95 | 1,1744 |
| Декабрь | 8,28 | 6,92 | 1,1970 |
| Январь | 5,46 | 6,89 | 0,7929 |
| Февраль | 5,88 | 6,85 | 0,8578 |
| Март | 6,93 | 6,82 | 1,0156 |
| Апрель | 4,62 | 6,79 | 0,6802 |
| Май | 3,78 | 6,76 | 0,5591 |
| Июнь | 3,99 | 6,73 | 0,5929 |
| Июль | 3,32 | 6,70 | 0,4956 |
| Август | 6,72 | 6,67 | 1,0078 |
| Сентябрь | 6,72 | 6,64 | 1,0126 |
| Октябрь | 7,77 | 6,61 | 1,1763 |
| Ноябрь | 8,19 | 6,57 | 1,2458 |
| Декабрь | 9,87 | 6,54 | 1,5085 |
| Итого | 35,999278 |
Рассчитаем средний индекс сезонности:
Большое значение индекса сезонности указывает на наличие сезонных колебаний.
