Випадок.
При додаванні та в ідніманні рац і ональн и х дроб ів в загальному випадку необх ідно в иконати наступні дії: 
1)розкладемо на множники кожний із знаменників, тобто винесемо спільний множник в знаменнику за дужки, розкладемо на множники за допомогою формул скороченого множення, способом групування, отримаємо
2) знайдемо наименший спільний знаменник, переписуємо перший, дивимося на другий знаменник і домножуємо на недостатні множники, потім третій і т. д, знаходимо до кожного дробу додатковий множник, ділимо спільний знаменник на кожний знаменник і знаходимо відповідний додатковий множник до кожного дробу, потім множимо додаткові множники на відповідні їм чисельники і записуємо весь отриманий вираз у чисельник:
В ЦЬОМУ ВИПАДКУ НЕ МОЖНА С КОРОЧУВАТИ ДУЖКИ З ЧИС ЕЛЬНИКА І ЗНАМЕ ННИКА!!!
необхідно розкрити дужки в чисельнику та записати отриманий вираз у чисельник, а знаменник залишити первісним:
2) після спрощення чисельника розкладаємо його на множники, щоб скоротити дріб:
Випадок
Приклад.
В цьому прикладі можна помітити, що при розкладанні на множники ще й кожного чисельника, отримаємо можливість скоротити кожний дріб та спростити приклад:
.
Приклад.
Приклад.
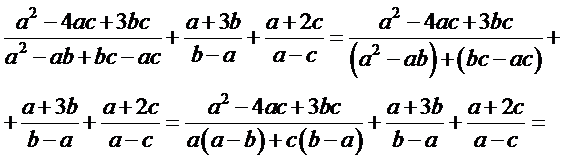
ЛІНІЙНІ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ З ПАРАМЕТРАМИ. ПЕРЕТВОРЕННЯ АЛГЕБРА ЇЧНИХ В И РА ЗІВ.
Рівняння з однією змінною можна привести до виду 
, де 
і 
- деякі числа (параметри), а 
-змінна. Розглянемо множину рішень лінійного рівняння:
- якщо 
, то - будь-яке число, 
,
- якщо 
, то рівняння не має коренів,
- якщо 
- будь-яке число, то 
.
Напри клад: 1) Розв ' язати рівняння:.
Рішення.
Приведемо дане рівняння до виду: 
;
;
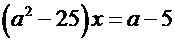; (1)
1) якщо 
і 
, то рівняння має одне рішення: 
;
;
2) якщо 
то
під час підстановки у рівняння (1),отримаємо:
якщо 
, то 
- невірна рівність і рівняння не має коренів;
якщо 
, то 
- вірна рівність і рівняння має безліч коренів.
Відповідь: якщо , то рівняння не має коренів;
якщо , то рівняння має безліч коренів;
якщо та , то .
2) Розв ' язати рівняння:
.
Рішення.
Запишемо рівняння у вигляді
;
;
;
; (2)
1) якщо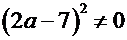 
та - будь-яке число 
; то рівняння має одне рішення
; 
.
2) якщо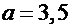 
та - будь-яке число, то під час підстановки значення 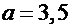в рівняння (2) отримаємо - вірна рівність та рівняння має безліч коренів.
Відповідь: при будь-якому значенні та 
; ;
при будь-якому значенні та 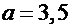; рівняння має безліч коренів.
3) Розв ' язати рівняння:
.
Рішення.
; (3)
1) якщо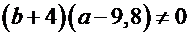 
то рівняння має одне рішення 
;
;
2) якщо 
, 
- будь-якечисло, то під час підстановки значення в рівняння (3) отримаємо 
- вірна рівність та рівняння має безліч коренів;
3) якщо 
, - будь-яке, то отримаємо 
, отже, при маємо - вірна рівність та рівняння має безліч коренів;
при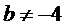 
маємо: , 
та рівняння не має коренів.
Відповідь: якщо 
, то ;
якщо та - будь-яке число або та 
, то рівняння має безліч коренів;
якщо 
та 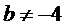, то рівняння не має коренів.
Розв ' язати рівняння:.
Рішення.
Дане рівняння може мати рішення при умові, якщо кожний з модулів дорівнює 0. Розв'яжемо систему:
Перше має рішення при будь-якому значенні параметра .
Розглянемо рішення другого рівняння.
Якщо 
та 
- будь-яке число, то 
,
якщо 
та 
, то 
, а при підстановці в перше рівняння отримаємо 
,
якщо та 
, то рішень немає.
Відповідь: якщо та - будь-яке число, то ,
якщо та , то та ,
якщо та , торішень немає.
Розв ' язати рівняння:.
Рішення.
Дане рівняння може мати рішення при умові, якщо кожний з модулів дорівнює 0. Розв'яжемо систему:
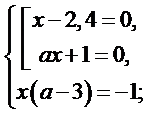
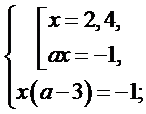
Розв'яжемо першу систему із сукупності:
з другого рівняння системи
якщо 
, то 
.
Щоб система мала рішення, необхідно, щоб 
. Розв'яжемо пропорцію та знайдемо значення параметра , при якому ця умова виконується.
, 
,
, 
, 
.
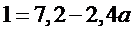Якщо 
, то при підстановці в друге рівняння першої системи отримаємо 
- невірна рівність, значить, рівняння та перша система не будуть мати рішень.
Розв'яжемо другу систему із сукупності:
1) 
якщо , то 
, якщо , то -невірна рівність, отже,рівняння не має коренів.
2) 
;
якщо 
, то 
; якщо 
, то отримаємо - невірна рівність, рівняння та друга система не має коренів.
Щоб друга система мала рішення, необхідно виконання умови: 
- невірна рівність та друга система не має рішень ні при яких значеннях параметра .
Відповідь: якщо 
, то рівняння має корінь 
;
якщо 
, то рівняння не має коренів.
За в дан ня. Розв'язати рівняння:
6. 
;
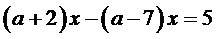7. 
;
8. 
;
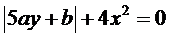9. 
;
10. 
;
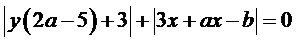11. 
;
12. 
;
13. 
.
