162. Коло, центр якого належить гіпотенузі прямокутного трикутника, дотикається більшого катета і проходить через вершину протилежного гострого кута. Знайдіть радіус кола, якщо катети 5см і 12см.
163. Точка дотику вписаного кола ділить гіпотенузу прямокутного трикутника на відрізки, один із яких на 14см більше іншого. Знайдіть площу трикутника, якщо радіус вписаного кола дорівнює 4см.
164. В колі по різні сторони від центра проведені дві паралельні хорди довжиною 16см і 32см, відстань між хордами 16см. Знайдіть радіус кола.
165. В колі по одну сторону від центра проведені дві паралельні хорди довжиною 48см і 24см, відстань між хордами 12см. Знайдіть радіус кола.
166. Гіпотенуза прямокутного трикутника 17см, медіана до одного з катетів  см. Знайдіть катети трикутника.
см. Знайдіть катети трикутника.
167. У прямокутному трикутнику медіани до катетів рівні 2  см і 4
см і 4  см. Знайдіть катети трикутника.
см. Знайдіть катети трикутника.
168. У прямокутному трикутнику АВС до гіпотенузи АВ проведена висота СМ. Площа трикутника АСМ дорівнює 6см  , площа трикутника ВСМ – 54см
, площа трикутника ВСМ – 54см  . Знайдіть сторони трикутника АВС.
. Знайдіть сторони трикутника АВС.
169. Катети прямокутного трикутника 6см і 8см. Знайдіть відстань від вершини меншого гострого кута трикутника до центра вписаного кола.
170. Перпендикуляр, проведений із точки кола до її діаметра, ділить його на два відрізки, різниця яких дорівнює 21см. Знайдіть довжину кола, якщо довжина перпендикуляра 10см.
171. Із точки А до кола проведені дві дотичні, відрізки яких 12см. Відстань між точками дотику 14,4см. Знайдіть радіус кола.
172. Із точки В до кола проведені дві дотичні, відстань між точками дотику 24см. Знайдіть відрізки дотичних, якщо радіус кола 15см.
173. Бічна сторона рівнобедреного трикутника точкою дотику вписаного кола ділиться у відношенні 9:8, рахуючи від вершини трикутника. Знайдіть площу трикутника, якщо радіус вписаного кола дорівнює 16см.
174. Бічна сторона рівнобедреного трикутника точкою дотику вписаного кола ділиться у відношенні 25:12, рахуючи від вершини трикутника. Знайдіть радіус вписаного кола, якщо площа трикутника 1680см  .
.
175. Радіус кола, вписаного в рівнобедрений трикутник, дорівнює 12см, відстань від центра цього кола до вершини трикутника 20см. Знайдіть периметр даного трикутника.
176. Висота рівнобедреного трикутника до основи дорівнює 18см, радіус вписаного кола 8см. Знайдіть периметр даного трикутника.
177. Висота рівнобедреного трикутника до основи дорівнює 20см, висота до бічної сторони 24см. Знайдіть площу даного трикутника.
178. У трикутнику АВС АВ=ВС, ВО і АМ - висоти трикутника, ВО:АМ=3:1. Знайдіть 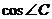 .
.
179. У трикутнику АВС АВ=ВС, ВЕ й СК - висоти трикутника,  . Знайдіть відношення СК:ВЕ.
. Знайдіть відношення СК:ВЕ.
180. Основа і бічна сторона рівнобедреного трикутника дорівнюють 20см і 30см відповідно. Знайдіть бісектрису кута при основі трикутника.
181. Коло, центр якого належить стороні АВ трикутника АВС, проходить через точку В, дотикається сторони АС у точці С і перетинає сторону АВ у крапці О. Знайдіть кути трикутника АВС, якщо АО:ОВ=1:2.
182. Коло, центр якого належить стороні МК трикутника МКЕ, проходить через точку К, дотикається сторони МЕ в крапці Е і перетинає сторону МК у точці О. Знайдіть кути трикутника МКЕ, якщо сторона МЕ дорівнює радіусу даного кола.
183. На сторонах АВ і АС трикутника АВС позначені точки М і К відповідно, МВ=6см, АК=4см, АС=18см. Знайдіть площу чотирикутника МВСК, якщо площа трикутника МАК дорівнює 15см  і
і  .
.
184. Одна зі сторін паралелограма дорівнює 12см, більша діагональ дорівнює 28см, тупий кут  . Знайдіть периметр паралелограма.
. Знайдіть периметр паралелограма.
185. Одна зі сторін трикутника 30см, інша сторона ділиться точкою дотику вписаного кола на відрізки 12см і 14см, рахуючи від кінця невідомої сторони. Знайдіть радіус вписаного кола.
186. Висота ромба 12см, менша діагональ 15см. Знайдіть площу ромба.
187. Знайдіть площу рівнобедреного трикутника, якщо висоти до бічної сторони і до основи відповідно дорівнюють 36см і 30см.
188. Знайдіть площу трапеції, основи якої 16см і 30см, бічні сторони 13см і 15см.
189. Основи рівнобічної трапеції 9см і 21см, висота 8см. Знайдіть радіус кола, описаного біля даної трапеції.
190. Основи рівнобічної трапеції 6см і 18см, діагональ 13см. Знайдіть радіус кола, описаного біля даної трапеції.
191. Знайдіть площу рівнобічної трапеції, основи якої 5см і 13см, а діагональ перпендикулярна бічній стороні.
192. Знайдіть радіус кола, описаного біля рівнобічної трапеції з основами 11см і 21см, і бічною стороною 13см.
193. Основи трапеції 2см і 7см, діагоналі дорівнюють 10см і 17см. Знайдіть площу трапеції.
194. Діагональ рівнобічної трапеції перпендикулярна бічній стороні і утворює із основою трапеції кут  . Знайдіть площу трапеції, якщо радіус описаного біля трапеції кола дорівнює R.
. Знайдіть площу трапеції, якщо радіус описаного біля трапеції кола дорівнює R.
195. Діагоналі трапеції взаємно перпендикулярні, одна з них дорівнює 48см, середня лінія трапеції 25см. Знайдіть висоту трапеції.
196. Діагональ рівнобічної трапеції перпендикулярна бічній
стороні і дорівнює 16см. Знайдіть площу трапеції, якщо радіус
описаного кола дорівнює 10см.
197. Діагоналі рівнобічної трапеції є бісектрисами гострих кутів і точкою перетину діляться у відношенні 5:13. Знайдіть площу трапеції, якщо висота дорівнює 90см.
198. Точка перетину бісектрис гострих кутів при основі трапеції належить іншій основі. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють 17см і 25см, а висота 15см.
199. Центр кола, описаного біля рівнобічної трапеції, лежить на її більшій основі. Знайдіть радіус цього кола, якщо діагональ трапеції дорівнює 20см, висота дорівнює 12см.
200. У рівнобічну трапецію вписано коло. Одна з бічних сторін точкою дотику ділиться на відрізки довжиною 4см і 9см. Знайдіть площу трапеції.
201. У рівнобічну трапецію вписано коло радіусом 12см. Одна з бічних сторін точкою дотику ділиться на відрізки, більший з яких дорівнює 16см. Знайдіть площу трапеції.
202. У прямокутну трапецію вписано коло. Точка дотику ділить більшу з бічних сторін трапеції на відрізки 16см і 36см. Знайдіть площу трапеції.
203. Площа рівнобічної трапеції дорівнює 36  см
см  , гострий кут
, гострий кут  . Знайдіть висоту трапеції, якщо в неї можна вписати коло.
. Знайдіть висоту трапеції, якщо в неї можна вписати коло.
204. Радіус кола, вписаного в рівнобічну трапецію, дорівнює 6см, одна з основ на 10см більше іншої. Знайдіть площу трапеції.
205. Центр кола, вписаного в прямокутну трапецію, вилучений від кінців її більшої основи на 15см і 20см. Знайдіть площу трапеції.
206. Коло, вписане в прямокутну трапецію, ділить точкою дотику більшу бічну сторону на відрізки 8см і 50см. Знайдіть площу трапеції.
207. Точка дотику кола, вписаного в прямокутну трапецію, ділить її більшу основу на відрізки 20см і 25см, рахуючи від вершини прямого кута. Знайдіть периметр трапеції.
208. Точка дотику кола, вписаного в прямокутну трапецію, ділить її меншу основу на відрізки 6см і 3см, рахуючи від вершини прямого кута. Знайдіть периметр трапеції.
209. Бісектриса кута А прямокутника АВСЕ ділить його сторону ВС на відрізки ВМ і МС довжиною 10см і 14см відповідно. Знайдіть відрізки, на які бісектриса ділить діагональ прямокутника.
210. Бісектриса кута А трикутника АВС ( ) ділить катет ВС на відрізки 6см і 10см. Знайдіть радіус кола, що проходить через точки А, С і точку перетину даної бісектриси з катетом ВС.
) ділить катет ВС на відрізки 6см і 10см. Знайдіть радіус кола, що проходить через точки А, С і точку перетину даної бісектриси з катетом ВС.
211. У прямокутному трикутнику МОК ( ) МО=18см, МК=30см. Знайдіть радіус кола, що проходить через точки М, О і точку перетину бісектриси кута М с катетом ОК.
) МО=18см, МК=30см. Знайдіть радіус кола, що проходить через точки М, О і точку перетину бісектриси кута М с катетом ОК.
212. Гіпотенуза прямокутного трикутника 39см, один з катетів 15см. Знайдіть бісектрису трикутника, проведену з вершини більшого гострого кута.
213. Діагональ рівнобічної трапеції ділить висоту, проведену з вершини тупого кута, на відрізки 15см і 12см, бічна сторона дорівнює меншій основі. Знайдіть площу трапеції.
214. Знайдіть площу прямокутного трикутника, якщо бісектриса прямого кута ділить гіпотенузу на відрізки 30см і 40см.
215. У рівнобедрений трикутник вписано коло, радіус якого 10см, точка дотику ділить бічну сторону на відрізки, які відносяться як 8:5, рахуючи від кута при вершині. Знайдіть площу трикутника.
216. Центр кола, вписаного в рівнобедрений трикутник, ділить його висоту до основи на відрізки 34см і 16см. Знайдіть площу даного трикутника.
217. Бісектриса кута прямокутника ділить його діагональ у відношенні 1:4. Знайдіть периметр прямокутника, якщо його площа 36см  .
.
218. У правильний трикутник АВС вписано квадрат МЕКР так, що вершини М і Р лежать на стороні АС, вершина Е - на стороні АВ, вершина К - на стороні ВС. Знайдіть сторону трикутника, якщо сторона квадрата 6см.
219. У рівнобедреному трикутнику АВС АВ=ВС=17см, ВО=15см - висота. Пряма, паралельна основі трикутника, перетинає сторони АВ і ВС у точках М і К відповідно і розбиває даний трикутник на дві рівновеликі частини. Знайдіть радіус описаного кола біля трикутника МВК.
220. Пряма, паралельна стороні АС трикутника АВС, перетинає його сторону АВ в точці М, сторону ВС в точці К. Знайдіть площу трикутника АВС, якщо ВМ=4см, АС=8см, АМ=МК, площа трикутника МВК дорівнює 5см  .
.
221. Із точки А, що не лежить на колі, проведені до неї дотична й січна. Відстань від точки А до точки дотику 16см, а до однієї із точок перетину січної з колом – 32см. Знайдіть радіус кола, якщо січна вилучена від центра на 15см.
222. Із зовнішньої точки до кола проведена січною довжиною 12см і дотична, довжина якої становить  внутрішнього відрізка січної. Знайдіть довжину дотичної.
внутрішнього відрізка січної. Знайдіть довжину дотичної.
223. Основа рівнобедреного трикутника 40см, висота до неї 15см. Знайдіть відстань між точками дотику кола, вписаного в даний трикутник, з її бічними сторонами.
224. Бічна сторона рівнобедреного трикутника 40см, висота до основи 4  см. Знайдіть відстань між точками перетину бісектрис кутів при основі трикутника з її бічними сторонами.
см. Знайдіть відстань між точками перетину бісектрис кутів при основі трикутника з її бічними сторонами.
225. У трикутнику АВС АВ=ВС=13см, АС=10см. До кола, вписаного в цей трикутник, проведена дотична, що паралельна основі АС і перетинає сторони АВ і ВС у точках М і К відповідно. Знайдіть площу трикутника МВК.
226. У трикутнику АВС медіани АМ і СК взаємно перпендикулярні і перетинаються в точці О. Знайдіть сторони трикутника, якщо АМ=9см і СК=12см.
227. Довжини сторін трикутника 11см, 12см, 13см. Знайдіть довжину медіани, проведеної до більшої сторони.
228. Дві сторони трикутника 15см і 25см, медіана до третьої сторони 16см. Знайдіть третю сторону трикутника.
229. ВМ - медіана трикутника АВС, ВМ=m,  ,
,  . Знайдіть сторону АВ.
. Знайдіть сторону АВ.
230. АК - медіана трикутника АВС, АС=а,  ,
,  . Знайдіть медіану АК.
. Знайдіть медіану АК.
231. О - точка перетину бісектрис трикутника АВС. Радіуси кіл, описаних біля трикутників АВС і АОС, дорівнюють 4  см і 12см відповідно. Знайдіть величину кута В.
см і 12см відповідно. Знайдіть величину кута В.
232. У трикутнику АВС точка О - центр вписаного кола. Знайдіть радіус описаного кола, якщо ВО=2  см, СО=3см,
см, СО=3см,  .
.
233. Точка М вилучена на 20см від центра кола, радіус якого 22см. Через цю точку проведена хорда довжиною 20см. Знайдіть відрізки, на які ділить точка М дану хорду.
234. Знайдіть зовнішній кут многокутника.

235. Два кола із центрами в точках В і С дотикаються внутрішнім чином з колом із центром у точці А і дотикаються одне з іншим зовні. Радіус більшого з кіл 12см. Знайдіть периметр трикутника АВС.
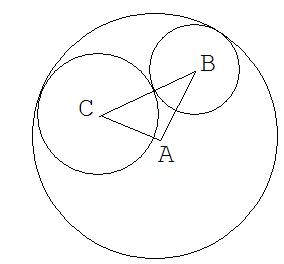
236. У прямокутнику АВСО прямі m і n проходять через точку перетину діагоналей. Площа фігури, що складається із трьох зафарбованих трикутників дорівнює 12см  . Знайдіть площу прямокутника АВСО.
. Знайдіть площу прямокутника АВСО.

237. У прямокутному трикутнику  , гіпотенуза
, гіпотенуза  ,
, 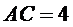 ,
,  . На стороні
. На стороні  лежить точка
лежить точка  .
. 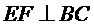 ,
,  ,
,  . Знайдіть площу прямокутника
. Знайдіть площу прямокутника  .
.
238. У ромбі 
 , висота дорівнює
, висота дорівнює  . На продовженні сторони
. На продовженні сторони  за точку
за точку  взята точка
взята точка 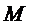 ,
,  . Відрізок
. Відрізок 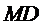 перетинає
перетинає  в точці
в точці  . У якому відношенні точка
. У якому відношенні точка  ділить відрізок
ділить відрізок  ?
?
239. У прямокутному трикутнику  , гіпотенуза
, гіпотенуза  , точка
, точка 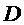 лежить на стороні АВ,
лежить на стороні АВ,  ,
,  ,
,  ,
,  . Знайдіть площу трикутника
. Знайдіть площу трикутника  .
.
240. Діагональ  прямокутника
прямокутника  дорівнює
дорівнює  і становить зі стороною
і становить зі стороною  кут
кут  . Сторона
. Сторона  продовжена за точку
продовжена за точку 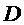 на відрізок
на відрізок  . Відрізок
. Відрізок  перетинає сторону
перетинає сторону  в точці
в точці  . У якому відношенні відрізок
. У якому відношенні відрізок  ділить сторону
ділить сторону  ?
?
241. У рівнобедрений трикутник вписано прямокутник, сторони якого відносяться як 1:3. Менша сторона прямокутника лежить на основі трикутника, а дві його вершини лежать на бічних сторонах трикутника. Сторони трикутника рівні 10, 10, 12см. Знайдіть площу прямокутника.
242. У прямокутному трикутнику  , гіпотенуза
, гіпотенуза  ,
, 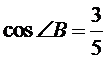 . Знайдіть співвідношення відрізків, на які бісектриса кута
. Знайдіть співвідношення відрізків, на які бісектриса кута  ділить катет
ділить катет  .
.
243. У рівнобедрений трикутник 
 вписано рівнобедрений прямокутний трикутник так, що вершина прямого кута лежить на основі даного трикутника, а гіпотенуза паралельна основі (вершини гострих кутів лежать на бічних сторонах трикутника). Знайдіть площу прямокутного трикутника, якщо висота
вписано рівнобедрений прямокутний трикутник так, що вершина прямого кута лежить на основі даного трикутника, а гіпотенуза паралельна основі (вершини гострих кутів лежать на бічних сторонах трикутника). Знайдіть площу прямокутного трикутника, якщо висота  .
.
244. У прямокутному трикутнику  , гіпотенуза
, гіпотенуза  ,
,  - бісектриса. Площі трикутників
- бісектриса. Площі трикутників 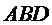 і
і  ставляться як 17:8. Знайдіть синус кута
ставляться як 17:8. Знайдіть синус кута  .
.
245. У прямокутному трикутнику гіпотенуза дорівнює 4, а кут  . У цей трикутник вписано прямокутник, у якого одна сторона у два рази більше іншої. Знайдіть площу прямокутника, якщо його більша сторона лежить на гіпотенузі, а дві вершини - на катетах.
. У цей трикутник вписано прямокутник, у якого одна сторона у два рази більше іншої. Знайдіть площу прямокутника, якщо його більша сторона лежить на гіпотенузі, а дві вершини - на катетах.

247. Кожна з бічних сторін рівнобедреного трикутника дорівнює 10см. На основі трикутника взята точка і проведені через неї дві прямі, паралельні бічним сторонам трикутника. Знайдіть периметр отриманого паралелограма.
248. Перпендикуляри, проведені із точки перетину діагоналей прямокутника, відносяться як 7:8, а його периметр дорівнює 60см. Знайдіть сторони прямокутника.
249. У прямокутнику  відстань від точки перетину діагоналей до прямої
відстань від точки перетину діагоналей до прямої  на 18см більше, ніж до прямої
на 18см більше, ніж до прямої  , а периметр прямокутника дорівнює 112см. Знайдіть сторони прямокутника.
, а периметр прямокутника дорівнює 112см. Знайдіть сторони прямокутника.
250. Висота ромба, що проведена з вершини тупого кута, ділить сторону ромба навпіл. Знайдіть периметр ромба, якщо довжина більшої діагоналі ромба дорівнює 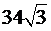 см.
см.
251. Сума двох кутів ромба дорівнює 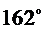 . Знайдіть кути одного із трикутників, на які ромб розбивається його діагоналями.
. Знайдіть кути одного із трикутників, на які ромб розбивається його діагоналями.
252. Тупий кут між діагоналями прямокутника дорівнює  . У скільки разів діагональ його більше меншої сторони?
. У скільки разів діагональ його більше меншої сторони?
253. Бісектриса тупого кута паралелограма ділить протилежну сторону у відношенні 7:13, починаючи від вершини тупого кута. Периметр паралелограма дорівнює 198 см. Знайдіть його сторони.
254. Бісектриса гострого кута паралелограма ділить протилежну сторону у відношенні 6:11, починаючи від вершини тупого кута. Периметр паралелограма дорівнює 184см. Знайдіть сторони паралелограма.
255. Довести, що протилежні вершини паралелограма розташовані на однаковій відстані від діагоналі, що з'єднує дві інші вершини.
256. На діагоналі  паралелограма
паралелограма  взяли точки
взяли точки 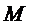 і
і  так, що
так, що  . Довести, що чотирикутник
. Довести, що чотирикутник  -
-
паралелограм.
257. У паралелограмі  висоти
висоти  і
і  ділять сторони
ділять сторони  і
і  на дві рівні частини. Знайти
на дві рівні частини. Знайти  .
.
258. Один з кутів паралелограма на 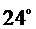 більше іншого. Знайти кут між висотами паралелограма, проведеними з вершини: 1) гострого кута; 2) тупого кута.
більше іншого. Знайти кут між висотами паралелограма, проведеними з вершини: 1) гострого кута; 2) тупого кута.
259. На дошці накреслили паралелограм  . Позначили середини сторін паралелограма. Потім витерли паралелограм, залишивши тільки середини сторін первісного паралелограма. Відновите початковий малюнок.
. Позначили середини сторін паралелограма. Потім витерли паралелограм, залишивши тільки середини сторін первісного паралелограма. Відновите початковий малюнок.
260. Бісектриси кутів  і
і  прямокутника
прямокутника  перетинаються в точці
перетинаються в точці  , що лежить на стороні
, що лежить на стороні  . Довести, що точка
. Довести, що точка  - середина
- середина  .
.
261. У прямокутнику  бісектриса кута
бісектриса кута  перетинає сторону
перетинає сторону  в крапці
в крапці  - середині
- середині  . Довести, що
. Довести, що  - бісектриса кута
- бісектриса кута  .
.
262. У рівнобедрений прямокутний трикутник, катет якого дорівнює 12см, вписано прямокутник, що має із трикутником спільний прямий кут. Знайдіть периметр прямокутника.
263. У рівнобедреному трикутнику 
 медіана
медіана  дорівнює половині сторони
дорівнює половині сторони  . Із точки
. Із точки 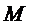 до сторін
до сторін  і
і  проведені перпендикуляри
проведені перпендикуляри  і
і  відповідно.
відповідно.  . Знайдіть довжину
. Знайдіть довжину  .
.
264. У паралелограмі  через точку перетину діагоналей проведена пряма, перпендикулярна діагоналі
через точку перетину діагоналей проведена пряма, перпендикулярна діагоналі  , що перетинає сторони
, що перетинає сторони  і
і  у точках
у точках  і
і  відповідно. Довести, що
відповідно. Довести, що 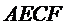 - ромб.
- ромб.
265.  - прямокутник,
- прямокутник,  - точка перетину діагоналей. Через точку
- точка перетину діагоналей. Через точку  проведені прямі, що перетинають сторони прямокутника
проведені прямі, що перетинають сторони прямокутника  і
і  у точках
у точках 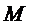 і
і  відповідно, а сторони
відповідно, а сторони  і
і  у точках
у точках  і
і  .
.  . Довести, що
. Довести, що  - ромб.
- ромб.
 266. У трикутнику
266. У трикутнику  провели відрізки
провели відрізки  і
і  , що перетинаються в точці
, що перетинаються в точці  . Точки
. Точки 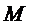 і
і  лежать на сторонах трикутника.
лежать на сторонах трикутника.  і
і 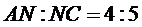 . Знайдіть відношення
. Знайдіть відношення
 .
.
267. На малюнку  ,
,  . Знайдіть відношення
. Знайдіть відношення  .
.
268. У трикутнику  відрізки
відрізки  і
і  перетинаються в точці
перетинаються в точці  .
.  ,
,  . Знайдіть відношення
. Знайдіть відношення  .
.
269. У рівнобедреному трикутнику 
 точка
точка 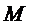 перетину медіан вилучена від вершини
перетину медіан вилучена від вершини  на 4см. Знайдіть відстань від середини бічної сторони до основи трикутника.
на 4см. Знайдіть відстань від середини бічної сторони до основи трикутника.
270. У рівносторонньому трикутнику  проведена медіана
проведена медіана  . Знайдіть відстань від точки
. Знайдіть відстань від точки 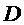 до сторони
до сторони  .
.
271. У прямокутному трикутнику  з гіпотенузою
з гіпотенузою 
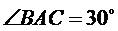 ,
, 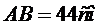 . Знайдіть відстань від середини катета
. Знайдіть відстань від середини катета  до гіпотенузи
до гіпотенузи  .
.
272. Точка  - середина катета
- середина катета  рівнобедреного прямокутного трикутника
рівнобедреного прямокутного трикутника  з гіпотенузою
з гіпотенузою  . Відстань від точки
. Відстань від точки  до гіпотенузи
до гіпотенузи  дорівнює 3см. Знайдіть гіпотенузу.
дорівнює 3см. Знайдіть гіпотенузу.
273. Діагоналі даного чотирикутника перпендикулярні і рівні 8см. Знайдіть периметр чотирикутника, вершини якого є серединами сторін даного чотирикутника, визначте його вид.
274. У чотирикутнику  кут між діагоналями
кут між діагоналями  і
і  дорівнює
дорівнює  ,
,  =
=  =10см. Знайдіть меншу діагональ чотирикутника, вершинами якого є середини сторін даного.
=10см. Знайдіть меншу діагональ чотирикутника, вершинами якого є середини сторін даного.
275. У чотирикутнику послідовно з'єднані середини сторін. З утвореним чотирикутником зробили те ж. Отриманий чотирикутник виявився ромбом. Доведіть, що діагоналі утвореного чотирикутника перпендикулярні.
276. У рівнобедреній трапеції один з кутів дорівнює  . Діагональ трапеції утворює з основою кут
. Діагональ трапеції утворює з основою кут  . Знайдіть основи трапеції, якщо довжина бічної сторони дорівнює 8см.
. Знайдіть основи трапеції, якщо довжина бічної сторони дорівнює 8см.
277. У рівнобедреній трапеції з тупим кутом  через вершину тупого кута проведена пряма, паралельна бічній стороні, що відтинає від більшої основи відрізок 12см. Знайдіть периметр трапеції, якщо менша основа дорівнює 16см.
через вершину тупого кута проведена пряма, паралельна бічній стороні, що відтинає від більшої основи відрізок 12см. Знайдіть периметр трапеції, якщо менша основа дорівнює 16см.
278. Діагональ трапеції ділить середню лінію на відрізки, один із яких на 5см більше іншого. Знайдіть більшу основу трапеції, якщо менша дорівнює 6см.
279. Довжини відрізків, на які діагональ трапеції ділить середню лінію, відносяться як 3:7. Знайдіть основи трапеції, якщо їхня різниця дорівнює 32см.
280. Більша основа трапеції відноситься до середньої лінії як 9:7. Середня лінія більше меншої основи на 64см. Знайдіть основи трапеції.
281. У прямокутній трапеції  з основами
з основами  і
і  , діагональ
, діагональ  , перпендикулярна бічній стороні
, перпендикулярна бічній стороні  і ділить кут
і ділить кут  у відношенні 2:1, рахуючи від більшої основи. Знайдіть середню лінію трапеції.
у відношенні 2:1, рахуючи від більшої основи. Знайдіть середню лінію трапеції.
282. У прямокутній трапеції більша основа дорівнює 21см. Висота, проведена з вершини тупого кута, ділить середню лінію на відрізки, довжини яких відносяться як 3:2, рахуючи від меншої бічної сторони. Знайдіть меншу основу трапеції.
283. Продовження бічних сторін  і
і  трапеції
трапеції  перетинаються в точці
перетинаються в точці  . Знайдіть
. Знайдіть  , якщо
, якщо  ,
,  .
.
284. Продовження бічних сторін  і
і  трапеції
трапеції  перетинаються в точці
перетинаються в точці 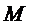 ,
,  . Знайдіть
. Знайдіть  , якщо
, якщо 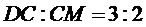 .
.
285. Точка перетину діагоналей трапеції ділить одну з діагоналей трапеції на відрізки довжиною 7см і 11см. Знайдіть основи трапеції, якщо їхня різниця дорівнює 16см.
286. Основи трапеції рівні 6см і 14см, а діагоналі – 15см і 20см. Знайдіть відрізки, на які кожна діагональ ділиться точкою перетину.
287. Периметри подібних трикутників відносяться як 2:5, а сума їхніх більших сторін дорівнює 56см. Знайдіть сторони трикутників, якщо сторони одного з них відносяться як 2:3:4.
288. Периметри подібних трикутників відносяться як 3:4, а сума їх більших за величиною сторін дорівнює 112см. Знайти сторони обох трикутників, якщо сторони одного з них відносяться як 4:8:7.
289. Визначте кути рівнобедреного трикутника, вписаного в коло, основа якого стягує дугу в  .
.
290. Визначте кути рівнобедреного трикутника, якщо бічна сторона стягує дугу в  .
.
 291. На малюнку
291. На малюнку  - діаметр кола з центром у точці
- діаметр кола з центром у точці  .
.
Знайдіть 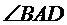 , якщо
, якщо  ,
,  .
.
292. На малюнку  - діаметр кола з центром у точці
- діаметр кола з центром у точці  . Знайдіть
. Знайдіть  , якщо
, якщо  ,
,  .
.
293. Дано точку, яка вилучена на відстані 7см від центра кола радіуса 11см. Через цю точку проведена хорда довжиною 18см. Знайдіть довжини відрізків, на які ділиться ця хорда даною точкою.
294. Дві хорди кола перетинаються в точці, що ділить одну хорду на відрізки довжиною 4см і 9см. На які відрізки ділиться друга хорда точкою перетину, якщо довжина другої хорди дорівнює 15см?
295. На продовженні діаметра  кола за точку
кола за точку  взята точка
взята точка 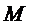 і через неї проведена дотична до кола із точкою дотику
і через неї проведена дотична до кола із точкою дотику  . Знайдіть кут
. Знайдіть кут  , якщо кут
, якщо кут  .
.
296. Навколо трикутника  описано коло. Через точку
описано коло. Через точку  до кола проведена дотична, а із точки
до кола проведена дотична, а із точки  на дотичну опущено перпендикуляр
на дотичну опущено перпендикуляр  . Знайдіть
. Знайдіть 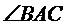 , якщо
, якщо  .
.
297. Із точки 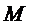 до кола проведена дотична
до кола проведена дотична  довжиною 6см і січна
довжиною 6см і січна  довжиною 12см. Знайдіть довжину відрізка
довжиною 12см. Знайдіть довжину відрізка  січної, розташованого поза колом.
січної, розташованого поза колом.
298. Із точки 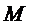 до кола проведена дотична
до кола проведена дотична  довжиною 6см і січна
довжиною 6см і січна  , відрізок
, відрізок  якої, що лежить поза колом, дорівнює 4см. Знайдіть довжину відрізка січної, розташованого у середині кола.
якої, що лежить поза колом, дорівнює 4см. Знайдіть довжину відрізка січної, розташованого у середині кола.
МАТЕРІАЛ З АЛГЕБРИ






