Доведення:
1 властивість) – доведітьсамостійно в зошиті.
2 властивість)
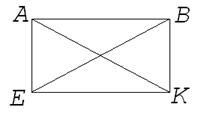
| Дано: АВКЕ – прямокутник, АК і ВЕ – діагоналі. Довести: АК=ВЕ. |
Доведення:
1. З  АКЕ і
АКЕ і  ВЕК – прямокутні (
ВЕК – прямокутні ( АЕК=
АЕК=  ВКЕ=90
ВКЕ=90  ):
):
АЕ = ВК – катети (за властивостями паралелограма),
ЕК – спільний катет.
Значить,  АКЕ =
АКЕ =  ВЕК за двома катетами, отже, АК = ВЕ.
ВЕК за двома катетами, отже, АК = ВЕ.
3 властивість)
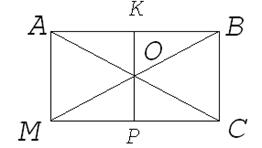
| Дано: АВСМ – прямокутник,
ВМ  АС=О, ОК АС=О, ОК  АВ, ОР АВ, ОР  СМ.
Довести: ОК=ОР. СМ.
Довести: ОК=ОР.
|
Доведення:
1. З 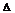 АКО і
АКО і  СОР – прямокутні (
СОР – прямокутні ( АКО=
АКО=  СРО=90
СРО=90  ):
):
ОА = ОС – гіпотенузи (за властивостями паралелограма),
 КАО =
КАО =  РСО (за властивістю внутрішніх різносторонніх кутів при АВ||СМ і січній АС). Значить,
РСО (за властивістю внутрішніх різносторонніх кутів при АВ||СМ і січній АС). Значить,  АКО=
АКО=  СОР за гострим кутом і гіпотенузою, отже, ОК=ОР.
СОР за гострим кутом і гіпотенузою, отже, ОК=ОР.
7. Ознаки прямо кут ника:
1) якщо в паралелограмі всі кути рівні, то він є прямокутник;
2) якщо в паралелограмі хоча б один кут прямий, то він є прямокутник;
3) якщо в паралелограмі діагоналі рівні, то він є прямокутник.
До ведення:
1 ознака) – доведітьсамостійно в зошиті.
2 ознака)

| Дано: АВСК – паралелограм,
 А= 90 А= 90  .
Довести: АВСК – прямокутник. .
Довести: АВСК – прямокутник.
|
Доведення:
1.  А+
А+  В=180
В=180  (за властивістю внутрішніх односторонніх кутів при АК||ВС і січній АВ), значить,
(за властивістю внутрішніх односторонніх кутів при АК||ВС і січній АВ), значить,  А=
А=  В=90
В=90  .
.
2. Аналогічно,  К=
К=  С=
С=  В=
В=  А= 90
А= 90  і АВСК – прямокутник (за означенням).
і АВСК – прямокутник (за означенням).
3 ознака)

| Дано: АВСР – паралелограм, АС=ВР – діагоналі. Довести: АВСР – прямокутник. |
Доведення:
1. З  АВР і
АВР і  РСА:
РСА:
АВ=СР (за властивостями паралелограма), АС=ВР (за умовою), АР–спільна сторона. Значить,  АВР=
АВР=  РСА за 3 ознакою рівності трикутників (за трьома сторонами). Отже,
РСА за 3 ознакою рівності трикутників (за трьома сторонами). Отже,  ВАР=
ВАР=  СРА.
СРА.
2.  СРА =
СРА =  АВС =
АВС =  ВАР =
ВАР =  ВСР (за властивостями кутів паралелограма).
ВСР (за властивостями кутів паралелограма).
3. АВСР – прямокутник (за першою ознакою прямокутника).
8. Ромб ( означення) – це паралелограм, у якого всі сторони рівні.
9. Властивості ромб а:
1) всі властивості паралелограма;
2) діагоналі ромба перпендикулярні і є бісектрисами його кутів.
До ведення:
1 властивість) – доведітьсамостійно в зошиті.
2 властивість)
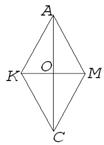
| Дано: АМСК – ромб,
КМ і АС – діагоналі.
Довести:1) КМ  АС,
2) АС – бісектриса АС,
2) АС – бісектриса  КАМ,
СА - бісектриса КАМ,
СА - бісектриса  КСМ,
КМ - бісектриса КСМ,
КМ - бісектриса  АКС,
МК – бісектриса АКС,
МК – бісектриса  АМС. АМС.
|
Доведення:
1. Нехай КМ  АС=О, КО=ОМ (за властивостями паралелограма), значить, АО – медіана
АС=О, КО=ОМ (за властивостями паралелограма), значить, АО – медіана  АКМ.
АКМ.
2. АК=АМ (АМСК – ромб) і  АКМ – рівнобедрений. Таким чином, КМ
АКМ – рівнобедрений. Таким чином, КМ  АС і АС – бісектриса
АС і АС – бісектриса  КАМ (за властивістю медіани рівнобедреного трикутника).
КАМ (за властивістю медіани рівнобедреного трикутника).
3. Аналогічно, СА – бісектриса  КСМ, КМ - бісектриса
КСМ, КМ - бісектриса  АКС, МК – бісектриса
АКС, МК – бісектриса  АМС.
АМС.
10. Ознаки ромб а:
1) якщо в будь – якому чотирикутнику всі сторони рівні, то цей чотирикутник є ромб;
2) якщо в паралелограмі діагоналі перпендикулярні, то він є ромб.
До ведення:
1 ознака) – доведітьсамостійно в зошиті.
2 ознака)

| Дано: КЕАС – паралелограм,
КА і СЕ – діагоналі,
КА  СЕ.
Довести: КЕАС – ромб. СЕ.
Довести: КЕАС – ромб.
|
Доказательство:
1. Нехай КА  СЕ=О.
СЕ=О.
2. З  КСО і
КСО і  КЕО – прямокутні (КА
КЕО – прямокутні (КА  СЕ):
СЕ):
КО – спільний катет, СО = ОЕ (за властивостями паралелограма), значить,  КСО =
КСО =  КЕО за двома катетами. Таким чином, СК = КЕ.
КЕО за двома катетами. Таким чином, СК = КЕ.
3. СК=АЕ, КЕ=СА (за властивостями паралелограма).
4. КЕАС – ромб (за означенням).
11. Квадрат ( означення) – це прямокутник, у якого всі сторони рівні або ромб, у якого всі кути прямі.
12. Властивості квадрат а: всі властивості прямокутника і ромба.
13. Ознаки квадрата: якщо діагоналі прямокутника перетинаються під прямим кутом, то він є квадрат.
14. Трапеція – це чотирикутник, у якого дві протилежні сторони паралельні, а дві інші непаралельні.
Паралельні сторони – основи, непаралельні – бічні сторони.
15. Рівнобічна трапеція – трапеція, у якій бічні сторони рівні.
16. Прямокутна трапеція – трапеція, у якій одна бічна сторона перпендикулярна основам.
Завдання. Зобрази в зошиті різні трапеції і вкажи їх елементи.
17. Висота трапеції – довжина перпендикуляра, проведеного з вершини однієї основи до другої основи. Всі відстані між основами трапеції чисельно дорівнюють висоті.

| АО – висота, ЕL=АО, ЕL –відстань між АВ і КС. |
18. Середня лінія трикутника (означення) – відрізок, який з¢єднує середини двох сторін трикутника.
19. Теорема Фалеса. Якщо паралельні прямі, які перетинають сторони кута або дві дані прямі, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні.

| Дано:
 (ab), А (ab), А  В В  || А || А  В В  || А || А  В В  .
А .
А  А А  = А = А  А А  .
Довести: В .
Довести: В  В В  = В = В  В В  . .
|
Доведення:
1. Проведемо через т.В  пряму ЕК||А
пряму ЕК||А  А
А  .
.
2. А  А
А  =КВ
=КВ  і А
і А  А
А  =В
=В  Е (за властивістю паралелограма).
Е (за властивістю паралелограма).
3. Отже, КВ  =В
=В  Е.
Е.
4. З  В
В  В
В  К і
К і  В
В  В
В  Е:
Е:
КВ  =В
=В  Е,
Е,  В
В  В
В  К=
К=  В
В  В
В  Е (за властивістю вертикальних кутів),
Е (за властивістю вертикальних кутів),  В
В  КВ
КВ  =
=  В
В  ЕВ
ЕВ  (за властивістю внутрішніх
(за властивістю внутрішніх
різносторонніх кутів при А  В
В  ||А
||А  В
В  і січній КЕ).
і січній КЕ).
Значить,  В
В  В
В  К=
К=  В
В  В
В  Е за 2 ознакою рівності трикутників (за стороною і прилеглими до неї кутами). Таким чином, В
Е за 2 ознакою рівності трикутників (за стороною і прилеглими до неї кутами). Таким чином, В  В
В  =В
=В  В
В  .
.
20. Теорема пр о пропорц ійні відрізки. Паралельні прямі, які перетинають сторони кута, відтинають від сторін кута пропорційні відрізки.

|  = = 
|
21. Властивість середньої лінії трикутника – вона паралельна третій стороні і дорівнює її половині.
(доведення проведи самостійно в зошиті)
22. Середня лінія трапеції (означення) – відрізок, який з¢єднує середини бічних сторін трапеції.
23. Властивість середньої лінії трапеції – вона паралельна основам і дорівнює їх півсуммі. 

| Дано: АВКС – трапеція (АВ||СК),
ОЕ – середня лінія.
Довести:
1)ОЕ || АВ ||СК,
2) ОЕ =  (АВ + СК). (АВ + СК). 
|
Доведення:
1. Проведемо пряму ВО, утворимо промінь КС, ВО  КС = Р.
КС = Р.
2. З  АВО і
АВО і  СРО:
СРО:
АО = ОС (ОЕ – середня лінія),  АОВ=
АОВ=  СОР (за властивістю вертикальних кутів),
СОР (за властивістю вертикальних кутів),  ВАО =
ВАО =  ОСР (за властивістю внутрішніх різносторонніх кутів при АВ || РК і січній РВ).
ОСР (за властивістю внутрішніх різносторонніх кутів при АВ || РК і січній РВ).
Значить,  АВО =
АВО =  СРО за 2 ознакою рівності трикутників (за стороною і двома прилеглими до неї кутами). Таким чином, АВ = РС.
СРО за 2 ознакою рівності трикутників (за стороною і двома прилеглими до неї кутами). Таким чином, АВ = РС.
3. ОЕ – середня лінія  РВК,
РВК,
ОЕ =  РК=
РК=  (РС + СК)=
(РС + СК)=  (АВ + СК) і
(АВ + СК) і
ОЕ||АВ||СК (за властивістю середньої лінії трикутника).
24. Властивості рівнобічної трапеції:
1) кути при основі рівні;
2) діагоналі рівні;
3) тільки навколо рівнобічної трапеції можна описати коло, центр цього кола – точка перетину серединного перпендикуляра до основи і бічної сторони трапеції;
4) тільки в рівнобічній трапеції

| АВКС – рівнобічна трапеція, (АВ||СК)
АЕ – висота трапеції,
ЕК =  (АВ + СК) (АВ + СК)
|
Доведення властивостей:
1 властивість)

| Дано: АВКС – рівнобічна трапеція, (АВ||СК)
Доказать:  С = С =  К. К.
|
Доведення:
1. Проведемо АЕ  СК, ВО
СК, ВО  СК.
СК.
2. З  АСЕ і
АСЕ і  ВКО - прямокутні (
ВКО - прямокутні ( АЕC =
АЕC =  ВОК = 90
ВОК = 90  ):
):
АС = ВК (АВКС – рівнобічна трапеція), АЕ = ВО (висоти трапеції).
Значить,  АСЕ =
АСЕ =  ВКО за гіпотенузою і катетом. Отже,
ВКО за гіпотенузою і катетом. Отже,  С=
С=  К.
К.
2 властивість)

| Дано: АВКС – рівнобічна трапеція, (АВ||СК) АК і ВС – діагоналі. Довести: АК = ВС. |
Доведення:
З  АКС і
АКС і  ВСК:
ВСК:
АС = ВК (АВКС – рівнобічна трапеція), СК – спільна сторона,  АСК=
АСК=  ВКС (за властивістю кутів рівнобічної трапеції).
ВКС (за властивістю кутів рівнобічної трапеції).
Значить,  АКС =
АКС =  ВСК за 1 ознакою рівності трикутників (за двома сторонами і кутом між ними). Таким чином, АК=ВС.
ВСК за 1 ознакою рівності трикутників (за двома сторонами і кутом між ними). Таким чином, АК=ВС.
3 властивість) якщо коло можна описати навколо трапеції, то воно буде описаним і навколо трикутника, вершини якого – вершини трапеції, пригадай, що є центром цього кола.
4 властивість)

| Дано: АВКС – рівнобічна трапеція, (АВ||СК)
АЕ – висота трапеції,
Довести: ЕК =  (АВ + СК) (АВ + СК)
|
Доведення:
1. Проведемо ОР – середню лінію трапеції, проведемо ОЕ.
2. Проведемо ОМ  СЕ. Так як АЕ
СЕ. Так як АЕ  СЕ, то ОМ || АЕ.
СЕ, то ОМ || АЕ.
О – середина АС, то М – середина СЕ (за теоремою Фалеса).
3. З  ОСМ і
ОСМ і  ОЕМ – прямокутні (
ОЕМ – прямокутні ( ОМC=
ОМC=  ОМЕ=90
ОМЕ=90  ):
):
ОМ – спільний катет, СМ=МЕ – катети.
Значить,  ОСМ=
ОСМ=  ОЕМ за двома катетами.
ОЕМ за двома катетами.  С=
С=  К (за властивостями кутів рівнобічної трапеції).
К (за властивостями кутів рівнобічної трапеції).
Отже,  ОСМ=
ОСМ=  ОЕМ=
ОЕМ=  РКС – відповідні кути при ОЕ і РК, і січній СК.
РКС – відповідні кути при ОЕ і РК, і січній СК.
ОЕ||РК (за ознакою паралельності прямих).
4. ОР||СК (за властивістю середньої лінії).
5. ОРКЕ – паралелограм (за означенням), отже,
ЕК=ОР=  (АВ + СК) (за властивістю середньої лінії трапеції).
(АВ + СК) (за властивістю середньої лінії трапеції).
25. Властивість трапеції: в трапецію можна вписати коло, якщо суми протилежних сторін трапеції рівні.

26. Чотирикутник (многокутник), описаний навколо кола – це чотирикутник (многокутник), всі сторони якого є дотичні до кола.
27. Чотирикутник, (многокутник) вписаний в коло – це чотирикутник,(многокутник), в якомуколо проходить через всі вершини чотирикутника.
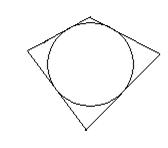
| 
|
28. Плоский кут – кожна з частин, на яку кут розбиває всю площину.

| Утворені два плоских кути – гострий і тупий. |
29. Доповняльні – плоскі кути із спільними сторонами.
30. Центральний кут – плоский кут з вершиною в центрі кола.

 АОВ – центральний кут.
АОВ – центральний кут.
31. Дуга кола – частина кола, яка розташована всередині відповідного плоского кута.
32. Градусна міра дуги – градусна міра відповідного центрального кута.
33. Кут, вписаний у коло: вершина кута лежить на колі, а сторони кута перетинають коло. Центральний кут, який відповідає тій дузі кола, яка не містить точку  , називається відповідним центральним кутом щодо вписаного кута.
, називається відповідним центральним кутом щодо вписаного кута.

 KLM –вписаний кут.
KLM –вписаний кут.
34. Властивості вписаного кута:

 1) він дорівнює половині відповідного центрального кута;
1) він дорівнює половині відповідного центрального кута;
якщо  ВАС – вписаний,
ВАС – вписаний,  ВОС – центральний, спираються на дугу ВnC, точки О і А лежать по одну сторону від хорди ВС, то
ВОС – центральний, спираються на дугу ВnC, точки О і А лежать по одну сторону від хорди ВС, то  ВАС=
ВАС= 
 ВnС=
ВnС= 
 ВОС.
ВОС.  ВАС – гострий.
ВАС – гострий.
Якщо А і О лежать по різні сторони від хорди ВС, то  ВАС – тупий та
ВАС – тупий та
 ВАС=180
ВАС=180 

 ВОС.
ВОС.
В цьому випадку відповідний центральний кут буде дорівнювати градусній мірі більшій дузі з двох, на які розбито коло точками В і С.
Доведення:
 Дано: коло (О; ОК),
Дано: коло (О; ОК),  AKМ - вписаний,
AKМ - вписаний,
 AOМ - центральний.
AOМ - центральний.
Довести:  AKМ=
AKМ= 
 AOМ.
AOМ.
Доведення.
1.  AON=
AON=  AKO +
AKO +  KAO (за властивістю зовнішнього кута трикутника АКО),
KAO (за властивістю зовнішнього кута трикутника АКО),  АОК - рівнобедрений (ОК=ОА) і
АОК - рівнобедрений (ОК=ОА) і  AKO=
AKO=  KAO (за властивістю кутів рівнобедреного трикутника), значить,
KAO (за властивістю кутів рівнобедреного трикутника), значить,  AKN=
AKN= 
 AON.
AON.
2. Аналогічно,  МKN=
МKN= 
 МON.
МON.
3. Отже,  AKМ=
AKМ=  AON+
AON+  МKN=
МKN= 
 AON+
AON+ 
 МON=
МON= 
 AOМ
AOМ
 2) 2)
| Вписані кути, сторони яких проходять через дві точки кола А і В, вершини яких лежать по одну сторону від прямої АВ, рівні між собою; Доведіть самостійно в зошиті. |
3) кути, які спираються на діаметр, прямі;
доведіть самостійно в зошиті. 
35. Обчислення градусних мір дуг кіл:
1)

| Дано: коло(О; ОС), ВА – дотична, ВС - січна
Довести:  АВС = АВС =   ВnС.
Доведення.
1. ВnС.
Доведення.
1.  ОВА=90 ОВА=90  (ВА – дотична).
2. (ВА – дотична).
2.  АВС= 90 АВС= 90  - -  ОВС=90 ОВС=90  - -  (180 (180  - -  ВОС) =
= 90 ВОС) =
= 90  - 90 - 90  + +   ВОС= ВОС=   ВОС= ВОС=   ВnС. ВnС.
|
2)

| АВ і СК – хорди, АВ  СК=Е, СК=Е,
 АЕС= АЕС=  КЕВ= КЕВ=  ( ( АnС+ АnС+  КmВ).
Доведіть самостійно в зошиті. КmВ).
Доведіть самостійно в зошиті.
|
3)

| АС і ВМ – січні, які перетинають коло в точках А, В, С, М,
АС  ВМ=К, ВМ=К,
 АКВ= АКВ=  ( ( АnВ- АnВ-  СmМ).
Доведіть самостійно в зошиті. СmМ).
Доведіть самостійно в зошиті.
|
36. Властивості хорд:
1)

| Якщо хорди АС і ВК кола перетинаються в точці Е, то
 . .
|
2)

| Якщо з точки К проведено до кола дві січних АС і ВМ, які перетинають коло в точках А, В, С, М, то 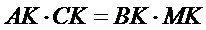 . .
|
ПОДІБНІСТЬ ТРИКУТНИКІВ.
Перетворення подібності.
Перетворенняфігури F у фігуру F  називається перетворенням подібності, якщо при цьому перетворенні відстань між точками первісної фігури відповідно змінюється в одну і ту ж кількість разів.
називається перетворенням подібності, якщо при цьому перетворенні відстань між точками первісної фігури відповідно змінюється в одну і ту ж кількість разів.
| X  Y Y  = k = k  XY, де
X XY, де
X  і Y і Y  - точки фигури F - точки фигури F  , X і Y – відповідні точки фигури F, k – коефіцієнт подібності. , X і Y – відповідні точки фигури F, k – коефіцієнт подібності.
|
Гомотетія.

| F – задана фігура, F 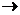 F F  , О – фіксована точка, А, В, С – вершини , О – фіксована точка, А, В, С – вершини  АВС, А АВС, А  А А  , В , В  В В  , С , С  С С  . .
 = =  = =  = k.
Таке перетворення фігури F в фігуру F = k.
Таке перетворення фігури F в фігуру F  називається гомотетією відносно центра О. називається гомотетією відносно центра О.
|






