tg  =
=  , 1 + tg
, 1 + tg 
 =
=  , cos (90
, cos (90  -
-  ) = sin
) = sin  ,
,
ctg  =
=  , 1 + ctg
, 1 + ctg 
 =
= 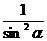 , tg (90
, tg (90  -
-  ) = ctg
) = ctg  ,
,
sin 
 + cos
+ cos 
 = 1, sin (90
= 1, sin (90  -
-  ) = cos
) = cos  , ctg (90
, ctg (90  -
-  ) = tg
) = tg  ,
,
tg (180  -
-  ) = - tg
) = - tg  , sin (180
, sin (180  -
-  ) = sin
) = sin  ,
,
cos (180  -
-  ) = - cos
) = - cos  ;
;  ;
;  або
або  .
.
11.
Кути  функції
функції
| 0 
| 30 
| 45 
| 60 
| 90 
|
| sin | 0 | 
| 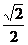
| 
| 1 |
| cos | 1 | 
| 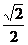
| 
| 0 |
| tg | 0 | 
| 1 | 
| ---- |
| ctg | ----- | 
| 1 | 
| 0 |

МНОГОКУТНИКИ.
ПЛОЩІ МНОГОКУТНИКІВ.
1. Ламана – фігура, яка складається з точок і послідовно з¢єднуючих їх відрізків.Точки – вершини ламаної, відрізки – ланки.
2. Проста л а мана – ламана, яка не має самоперетину.
3. Довжина л а мано ї – сума довжин її ланок.
4. Властивість л а мано ї. Довжина ламаної не менше довжини відрізка, який з¢єднує її кінці.
5. Замкнута л а мана – ламана, кінці якої збігаються.
6. Много кутник – проста замкнута ламана. Вершини ламаної – вершини многокутника, ланки ламаної – сторони многокутника (ніякі три вершини не лежать на одній прямій).
7. Плоский много кут ник – кінечна частина площини, яка обмежена многокутником.
8. О пукл и й много кут ник - многокутник, який лежить в одній півплощині відносно будь-якої прямої, яка містить його сторону.
9. Зовнішній кут опуклого многокутника при даній вершині - кут, суміжний з внутрішнім кутом многокутника при даній вершині.

|
 ВСЕ – зовнішній. ВСЕ – зовнішній.
|
10. Властивості кутів о пуклого n – кут ника:
1) сума внутрішніх кутів опуклого n – кутника дорівнює
180 
 (n – 2);
(n – 2);
2) сума зовнішніх кутів опуклого n – кутника, взятих по одному при кожній вершині, дорівнює 360  .
.
11. Правильн и й много кут ник – опуклий многокутник, у якого всі сторони і кути рівні. Градусна міра внутрішнього кута правильного n - кутника дорівнює  .
. 
12. Центр правильного много кут ника – центр описаного навколо многокутника кола і вписаного кола у многокутник.
13. Центр вписан ого кола в трапецію і ромб лежить на середині висоти (висота дорівнює діаметру).
Правильн і n – кут ники под і бн і.
15. Властивість. Якщо чотирикутник описано навколо кола, то суми протилежних сторін рівні між собою и навпаки, якщо у будь-якого чотирикутника суми протилежних сторін рівні між собою, то в цей чотирикутник можна вписати коло.
Кількість діагоналей опуклого n -кутника, проведених з однієї вершини:.
17. Загальна кількість діагоналей опуклого n -кутника:
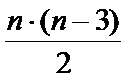 .
.
18. Властивості:
1. Відношення периметрів подібних правильних многокутників дорівнює відношенню радіусів описаних кіл і вписаних, і дорівнює відношенню їх відповідних лінійних розмірів.
2. Відношення площ подібних правильних многокутників дорівнює квадрату відношення відповідних лінійних розмірів цих многокутників.
19. Формули радіусів вписаних і описаних кіл правильних многокутників:
| Кількість сторін | радіус описаного кола (R) | радіус вписаного кола (r) | сторона многокутника |
| n | 
| 
| 
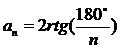
|
| n=3 | 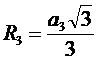 
| 
| 

|
| n=4 |  
| 
| 

|
| n=6 | 
| 
| 

|
20. Довжина кола та його частин:  ,
,  ,
,
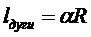 , де
, де  - радіанна міра відповідного центрального кута,
- радіанна міра відповідного центрального кута,  ,де
,де  - градусна міра центрального кута.
- градусна міра центрального кута.
21. Радіанна міра кутів:

| 
| 
| 
| 
|

| 
| 
| 
| 
|
Площі многокутників.
1) паралелограм і трапеція:
 S = ab
S = ab
| 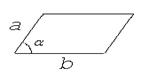 S = ab sin
S = ab sin 
|  S = ah
S = ah
|  S =
S =  d d  d d  sin sin 
|
Ромб
 S = a
S = a  sin sin 
|  S =
S =  d d  d d 
| Для квадрату:
S = а  , S = , S =  d d  ,
d = а ,
d = а  , а = , а = 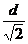 . .
|  S = S =  (a +b) h (a +b) h
|
2) тр икут ник:
S=  ab – прямокутного, S=
ab – прямокутного, S=  ab sin
ab sin  , S=
, S=  ah,
ah,
S=  a
a  sin
sin  - для рівнобедреного трикутника, S =
- для рівнобедреного трикутника, S =  а
а  - для рівнобедреного прямокутного трикутника,
- для рівнобедреного прямокутного трикутника,
S = 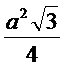 - для рівностороннього трикутника,
- для рівностороннього трикутника,
S =  , де р – півпериметр трикутника (формула Герона),
, де р – півпериметр трикутника (формула Герона),
S = 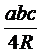 , де a, b, c – сторони, R – радіус описаного кола,
, де a, b, c – сторони, R – радіус описаного кола,
S = pr, де r – радіус вписаного кола, p – півпериметр.
3) площа будь-якого чотирикутника: S =  d
d  d
d  sin
sin  , де d
, де d  ,d
,d  - діагоналі,
- діагоналі,  - кут між діагоналями.
- кут між діагоналями.
4) площа будь-якого многокутника: S = pr, де r – радіус вписаного кола, p – півпериметр.
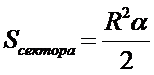 5) площа круга і його частин:
5) площа круга і його частин:

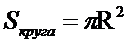 ,
,  ,
,
де n - градусна міра відповідного центрального кута або
 - радіанна міра відповідного центрального кута.
- радіанна міра відповідного центрального кута.
 площа кругового сегменту:
площа кругового сегменту:  ,
,
якщо 

 , якщо
, якщо 
23. Наслідок з теореми Менелая. Якщо точки  і
і 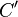 лежать відповідно на сторонах
лежать відповідно на сторонах 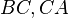 і
і  трикутника
трикутника 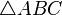 або на їх продовженнях, то наслідком є відношення довжин
або на їх продовженнях, то наслідком є відношення довжин 







