4. Властивості перетворення подібності:
1) перетворення подібності переводить прямі у прямі, півпрямі у півпрямі, відрізки у відрізки;
2) перетворення подібності зберігає кути між півпрямими;
5. Два трикутника називаються подібними, якщо вони переводяться один в одного за допомогою перетворення подібності ( ).
).
6. Властивості подібних трикутників:
1) у подібних трикутників відповідні кути рівні, відповідні відрізки пропорційні.
2) відношення периметрів подібних трикутників дорівнює відношенню відповідних сторін і дорівнює коефіцієнту подібності;
3) відношення площ подібних трикутників дорівнює квадрату коефіцієнта подібності.
7. Ознаки подібності трикутників:
1) за двома кутами (якщо два кути одного трикутника дорівнюють двом кутам другого трикутника, то ці трикутники подібні);
2) за двома сторонами і кутом між ними (якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, які утворені цими сторонами, рівні, то трикутники подібні.
3) за трьома сторонами (якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники подібні).
Доведення:
1 ознака)

| Дано:  АВС і АВС і  А А  В В  С С  , ,
 В= В=  В В  , ,  А= А=  А А  .
Довести: .
Довести:  АВС АВС   А А  В В  С С  . .
|
Доведення:
1. Нехай  =
=  , побудуємо
, побудуємо  А
А  В
В  С
С  , гомотетичний до
, гомотетичний до  А
А  В
В  С
С  відносно центра О, з коефіцієнтом гомотетії
відносно центра О, з коефіцієнтом гомотетії 
 А
А  В
В  С
С 
 А
А  В
В  С
С  .
. 
2.  А
А  =
=  А
А  ,
,  В
В  =
=  В
В  (за властивостями подібних трикутників), таким чином,
(за властивостями подібних трикутників), таким чином,  В=
В=  В
В  ,
,  А=
А=  А
А  .
.
3. А  В
В  = k
= k  А
А  В
В  = АВ, значить,
= АВ, значить,  АВС =
АВС =  А
А  В
В  С
С  за 2 ознакою рівності трикутників (за стороною і двома прилеглими до неї кутами).
за 2 ознакою рівності трикутників (за стороною і двома прилеглими до неї кутами).
4. Отже,  АВС
АВС 
 А
А  В
В  С
С  .
.
Доведіть самостійно в зошиті 2 і 3 ознаки подібності трикутників.
8. Прямо кутні тр икут ники под ібні, якщо вони мають однаковий за градусною мірою гострий кут.
Співвідношення у прямо кутному тр икутнику.

|  АВС – прямокутний, АВ – гіпотенуза, СК – висота, тоді АВС – прямокутний, АВ – гіпотенуза, СК – висота, тоді  АКС і АКС і  ВКС – прямокутні. ВКС – прямокутні.
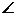 АСК = АСК = 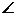 СВА, СВА, 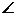 САК= САК= 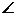 ВСК.
Вірними є рівності:
1. СА ВСК.
Вірними є рівності:
1. СА  = АК = АК  АВ
2. СВ АВ
2. СВ  = КВ = КВ  АВ
3. СК АВ
3. СК  = АК = АК  КВ КВ
|
АК – проекція катета АС на гіпотенузу АВ, КВ – проекція катета СВ на гіпотенузу АВ.
До ведення:
Так як  А= 90
А= 90  -
-  В=
В=  ВСК, то
ВСК, то  АВС
АВС 
 АСК
АСК 
 СВК (як прямокутні).
СВК (як прямокутні).
1. З  АВС
АВС 
 АСК:
АСК:  =
=  =
=  ,
,  =
= 
 СА
СА  =АК
=АК  АВ.
АВ.
2. З  АВС
АВС 
 СВК:
СВК:  =
=  =
=  ,
,  =
= 
 СВ
СВ  =КВ
=КВ  АВ.
АВ.
3. З  АСК
АСК 
 СВК:
СВК:  =
=  =
=  ,
,  =
= 
 СК
СК  =АК
=АК  КВ.
КВ.
10. Властивість б і сектрис и тр икут ника.
Бісектриса трикутника поділяє протилежну сторону на відрізки, пропорційні двом іншим сторонам.
 
| ВО – бісектриса  АВС, АВС,
 = =  .
Самостійне завдання: проведіть самостійно доведення цієї властивості і запишіть.
Довжину бісектриси, проведену до сторони, можна обчислити за формулою: .
Самостійне завдання: проведіть самостійно доведення цієї властивості і запишіть.
Довжину бісектриси, проведену до сторони, можна обчислити за формулою:
 , к і m - довжини відрізків, на які бісектриса поділяє третю сторону трикутника.
Формула медіани до сторони трикутника: , к і m - довжини відрізків, на які бісектриса поділяє третю сторону трикутника.
Формула медіани до сторони трикутника:


 . .
|






