Пусть 
комплект входных и выходных, соответственно, позиций перехода 
. Аналогично, ввод 
комплекты переходов, из которых дуги направлены в позиции, 
комплект переходов, в которые из позиции 
направлены дуги.
Рассмотрим классификацию сетей Петри по ограничениям, которые могут быть наложены на дуги графа сети Петри 
Общая сеть Петри - сеть Петри, на дуги ориентированного графа которой не наложено никаких ограничений.
Петля (loop) - пара, состоящая из позиции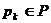 
и перехода 
, для которого позиция одновременно является входной и выходной позицией.
и 
| |  |
Чистая сеть Петри (self-loop-free Petri net) - общая сеть Петри 
, свободная от петель.
Чистая сеть Петри; не ординарная сеть Петри:
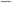
3 
.
| 
| 
| 
| 
| 
| |||
|
| 
| 
|
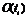
| -1 | -1 | 2 | ||
|
| 
| 
| 
|
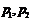
| 1 | -1 | ||
|
| 
| 
|
| 3 | -1 |
Таким образом, чистая сеть Петри может иметь кратные дуги, и ее структура может быть описана только одной составной матрицей изменения 
.
Сеть Петри с петлей (не чистая сеть Петри); ординарная сеть Петри:
 |  |  | |||
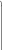
петля 
|
|
|
|
|
|
| |||
|
|
|
|
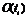
| 1 | 1 | |||
|
| 
| 
| 
|
| 1 | |||
|
|
|
|
| 1 |
|
|
|
|
|
|
| ||||
|
|
| -1 | -1 | ||||||
|
| 1 |
|
| 1 | -1 | |||
|
| 1 | 1 |
| 0 | 1 |
Для описания не чистых сетей Петри требуются обе матрицы инциденций 
.
Ординарная сеть Петри (ordinary Petri net) - общая сеть Петри , кратность всех имеющихся дуг которой равна единице.
Ординарная сеть Петри - это сеть Петри без кратных дуг, которая в общем случае может иметь петли.
Следовательно, в ординарных сетях Петри комплекты 
сводятся к множествам.
Простая сеть Петри (simple Petri net) - ординарная сеть без петель.
 |
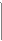
Включения введенных классов СП с помощью диаграмм Вини имеют вид (рис. 5.1):
Общая сеть Петри
Чистая СП Простая СП Ординарная СП
Рис. 5.1. Классы Сетей Петри
Сеть Петри со свободным выбором (ССВ) - простая сеть Петри такая, что: Если 
”
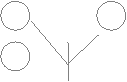
ССВ:
| 
| ||||
|
| { }
| ||||
|
| { }
|
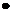
не ССВ:
|
|
| ||||
|
| { , }
| ||||
|
| { }
|
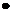
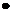
Сеть Петри со свободным выбором (свободна сеть Петри ССВ)) (free choice Petri net; FC - net) - простая сеть Петри, в которой для каждого перехода 
выполняется одно из следующих условий для любой его входной позиции 
(рис. 5.2):
– либо - единственная входная позиция перехода (т.е. позиция больше не связана с другими переходами);
|
– либо, если является входной позицией нескольких переходов
то она является единственной для этих переходов
(т.е. эти переходы больше не связаны ни с какими другими позициями).
 | |||
 | |||
 | |||
 | |||
 | |||
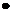
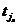
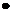
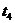
Рис. 5.2. Сеть Петри со свободным выбором
|
|
| ||||
|
| { , , }
| ||||
|
| { }
| ||||
|
| { }
|
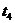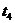Конфликтная позиция - позиция 
, которая является входной для нескольких переходов.
Автоматная сеть Петри (машина конечного состояния) (finite state-machine net) - простая сеть Петри, в которой каждый переход имеет ровно одну входную и ровно одну выходную позицию.
 |
 |
Автоматная сеть Петри(подкласс ССВ):
 |  | ||
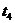
Заметим, что данная сеть Петри не является маркированным графом.
Сеть Петри, не являющаяся автоматной сетью Петри:
