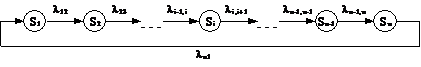Процесс гибели и размножения

Непрерывная Марковская цепь – представляет собой цепь гибели и размножения, если ее граф состояний представляет собой цепочку, в которой каждое из состояний S₂,..., S_n-1 связано с соседним прямой и обратной связью.

 

 

                                           = -l₁₂P₁(t) + l₂₁P₂(t)

                              = l_i-1,iP_i-1(t)+l_i+1,iP_i+1(t)–(l_i,i-1+l_i,i+1)P_i(t), i=2,n-1 (25)

                                        .    .    .    .    .

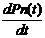                                   = l_n-1,nP_n-1(t) - l_n,n-1P_n(t)

В установившемся процессе

                                                                  = 0.                                     (26)

Циклический процесс

 

 

Непрерывная Марковская цепь называется циклическим процессом, если состояния связаны между собой в кольцо с односторонними переходами. Для этого случая система дифференциальных уравнений имеет вид:

                                        = -l₁₂P₁(t) + l_n1P_n(t)

                                       .    .    .    .    .

                                     = l_i-1,iP_i-1(t) - l_i,i+1P_i(t),     i=2,n-1          (27)

                                           .    .    .    .    .

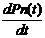                                          = l_n-1,nP_n(t) l_n1P_n(t)

Для стационарного процесса имеем систему алгебраических уравнений:

                                                                                               (28)

                       P₂= 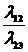P₁, P₃= P₂= P₁ Þ P_i= P₁, P_n= P₁        (29)

                       P1=[1+l₁₂( + +...+ )]^-1(из условия нормировки)       (30)

t_i=1/l_i,i+1 – среднее время пребывания системы в i-ом состоянии

                                                               P_i= t_i / .                                              (31)

Таким образом, предельные стационарные вероятности всех состояний этой системы, которая описывается циклическим графом, можно определить по заданным интенсивностям переходов в различные состояния системы.

Пример.

Рассмотрим систему обработки информации:

 

ИВС – источник входных слов, которые подлежат обработке в СВУ (специализированном вычислительном устройстве);

КПИ – канал передачи информации;

Б – буфер.

Пусть время передачи сигнала по КПИ представляет собой случайную величину, подчиненную показательному закону распределения с параметром l₁ – время передачи сообщения. Время обработки информации в СВУ – l₂.

Необходимо построить расчетную модель системы. Система может принимать n+3 возможных состояний.

S_-1 – в накопителе нет данных, СВУ простаивает, по КПУ идет заявка (работает);

S₀ – в Б нет данных, СВУ и КПИ – в режиме работы;

S_i – в Б имеется i сигналов, СВУ и КПИ – в режиме работы;

S_n – Б занят полностью, СВУ и КПИ – в режиме работы;

S_n+1 – буфер занят, СВУ работает, КПИ заблокирован.

 

Цепь Маркова имеет вид

 

Если ввести обозначение r = , то предельные вероятности состояний системы будут:

                               P_-1 =     P_i = rⁱ⁺¹P_-1, i = 1,n+1.                       (32)

 

Значения вероятностей позволяют определить основные характеристики системы: среднюю долю времени, в течение которого КПИ находился в состоянии простоя, и т.д.

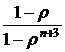                               P_n+1=      P₁=                    (33)

Не Марковские случайные процессы,

Сводящиеся к Марковским

Реальные процессы часто обладают последействием и поэтому не являются Марковскими. Иногда для исследования этих процессов удается использовать методы цепей Маркова. При этом для сведения не Марковских процессов к Марковским используют 2 метода:

– метод разложения случайного процесса на фазы (метод псевдосостояний);

– метод вложенных цепей Маркова.