Наиболее общим подходом формализованного описания функционирования систем является подход, предложенный Н.П.Бусленко, который позволяет описать поведение непрерывных и дискретных, детерминированных и стохастических систем – является универсальным.
Базируется этот подход на понятии агрегативной системы – А -схема. При агрегативном описании сложная система разбивается на конечное число частей, подсистем, сохраняя при этом связи обеспечивающие их взаимодействие. Эти подсистемы могут быть разбиты на более мелкие части и в результате такой декомпозиции сложные системы могут быть представлены в виде многоуровневых конструкций из взаимосвязанных элементов.
В качестве элемента А -схемы выступает агрегат, а связь между ними осуществляется с помощью оператора сопряжения R. Агрегат сам может рассматриваться как А -схема, то есть разбиваться на элементы (агрегаты) следующего уровня. Любой агрегат характеризуется множествами:
– моментов времени t,
– входных Х,
– выходных У,
– состояний Z в каждый момент времени.
Переход агрегата из состояния z1(t) в z2(t) (z1 
z2) происходит за малый интервал времени и при этом имеет место скачок D z изменения состояний. Этот скачок определяется внутренними параметрами агрегата h(t) Î H и входными сигналами 
Х. В начальный момент времени t0 состояние агрегата – z0. Пусть процесс функционирования агрегата в случае воздействия входного сигнала xn описывается случайным оператором V. Тогда в момент поступления в агрегат tn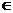 
T входного сигнала xn определяется состояние
z (tn +0) = V [ tn, z (tn), xn ]. (11)
Если на интервале времени [tn, tn+1] не содержится ни одного момента поступления сигнала, то для этого интервала времени состояние агрегата описывается оператором U:
z (t) = U [ t, tn, z (tn +0)]. (12)
Совокупность cлучайных операторов V и U рассматривается как оператор переходов агрегата в новое состояние. На оператор не накладывается никаких ограничений, поэтому допустимы скачки состояний D z в моменты времени, не являющиеся моментами поступления сигналов. Моменты скачков состояний без поступления входного сигнала d z называются особыми моментами времени t d, а состояния z(t d) – особые состояния А -схемы. Для описания этих скачков используется случайный оператор W
z (t d +0) = W [ t d, z (t d)], (13)
который является частным случаем оператора U.
На множестве состояний Z выделяется такое подмножество z(y), что если z(t d) достигает z(y), то состояние является моментом выдачи выходного сигнала и определяется оператором выходов G
y = G [ t d, z (t d)]. (14)
Таким образом, агрегат – это любой объект, определяемый упорядоченной совокупностью множеств T, X, Y, Z, Z(y), H и случайных операторов V, U, W, G. Последовательность выходных и входных сигналов, поступающих на А -схему, называется входным или Х -сообщением и выходным или У -сообщением.
Функционирование системы связано с переработкой информации. Передачи информации обозначаются на структуре А –схемы стрелками. Внешняя информация поступает от внешних объектов схемы, которые не являются элементами этой схемы, а внутренняя – от агрегатов. При этом обмен информации между А –схемой и внешней средой Е происходит через полюса схемы (агрегаты).
Различают входные (А1, А2, А3) и выходные полюса (А1, А3, А4, А5, А6).
Каждый n -й агрегат А -схемы имеет входные контакты, на которые поступает совокупность элементарных сигналов xi(t), 
, одновременно возникающих на входе элемента, и выходные контакты, с которых снимается совокупность элементарных сигналов yi(t), 
. Для построения А -схемы необходимо задать способы взаимодействия между агрегатами. Каждый n -й агрегат имеет In входных и Jn входных контактов. При этом функционирование агрегата может быть описано в виде взаимодействия агрегатов путем передачи информации от одного к другому.
Допущения:
– взаимодействие между А -схемой и внешней средой Е осуществляется путем передачи сигналов, причем взаимное влияние сигналов друг на друга не учитываются;
– для описания сигнала используется конечный набор характеристик;
– элементарные сигналы передаются в схеме мгновенно, независимо друг от друга по элементарным каналам;
– к входному контакту любого элемента А -схемы подключается не более 1 элементарного канала, а к выходному контакту – любое число элементарных каналов.
Внешняя среда Е представляется в виде фиктивного элемента А -cхемы – А0, вход которого содержит I0 входных контактов: 
, 
; 
, 
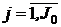
Сигнал, выдаваемый А -схемой во внешнюю среду Е, принимается агрегатом А0 как входной сигнал, состоящий из последовательности сигналов: 
. Сигнал, поступающий на А -схему из внешней среды Е, является выходным сигналом агрегата А0 
.
Каждый агрегат А -схемы характеризуется множеством входных контактов и множеством входных и выходных контактов { 
, 
} n = 0,NA, где NA - число агрегатов в схеме.
В силу предположения о независимости передачи сигналов каждому входному контакту 
соответствует не более чем один входной контакт 
, где 
- множество выходных контактов всех элементов А -схемы и внешней среды Е; 
- множество выходных контактов всех элементов А -схемы и внешней среды Е, с которой она связана элементарным каналом. Поэтому можно ввести однозначный оператор R, сопоставляющий каждому входному контакту выходной контакт, связанный с ним элементарным каналом. R – оператор сопряжения агрегатов в А -схему: 
=R(). Оператор сопряжения можно задать в виде таблицы, в которой на пересечении строк с номерами элементов и столбцов с номерами контактов i располагается пара чисел kl, указывающая номер элемента k и номер контакта l, с которым связан контакт 
[1].
| n | l | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 0 | 1,1 | 3,1 | 4,1 | 5,1 | 6,1 |
| 1 | 0,1 | - | - | - | - |
| 2 | 1,3 | 0,2 | 0,3 | - | - |
| 3 | 1,2 | 2,1 | - | - | - |
| 4 | 3,2 | 2,1 | 2,2 | - | - |
| 5 | 2,2 | - | - | - | - |
| 6 | 5,2 | 0,4 | - | - | - |
