Информационная система, как один из видов сложных систем, характеризуется:
1. Асинхронностью: отдельные подсистемы функционируют независимо, взаимодействуя друг с другом время от времени, при этом обычно трудно указать время начала и конца такого взаимодействия и его длительность, т.е. время взаимодействия подсистем никак не учитывается.
2. Недетерминированностью: подсистемы взаимодействуют в процессе функционирования системы в произвольные моменты времени, что делает поведение системы случайным (стохастическим), т.е. система при одних и тех же начальных условиях может функционировать по-разному, порождая не единственный процесс, а некоторое множество процессов.
3. Параллелизмом: несколько подсистем могут функционировать в системе одновременно, не влияя друг на друга (т.е. в системе могут протекать одновременно ряд параллельных процессов);
4. Конфликтностью: наличие в системе такой подсистемы, которая необходима для функционирования ряда других подсистем, но она может взаимодействовать с ними не одновременно, а только поочередно (либо с одной, либо с другой, но не вместе с обеими);
5. Синхронизацией: обеспечение такого взаимодействия конфликтующих систем, чтобы исключить “тупиковые ситуации”, связанные с невозможностью дальнейшего функционирования системы(т.е. согласование во времени нескольких систем, потребляющих общий ресурс).
Событие (event) 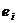 - некоторый факт в системе, трактуемый как потенциальное действие одной из ее подсистем, которое может реализоваться один раз, повториться многократно или не произойти ни разу.
- некоторый факт в системе, трактуемый как потенциальное действие одной из ее подсистем, которое может реализоваться один раз, повториться многократно или не произойти ни разу.
Пусть 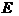 -множество событий, возможных в системе
-множество событий, возможных в системе  . Взаимосвязи между событиями вводятся не с помощью непосредственных связей между ними, а путем описания тех ситуаций, при которых данное событие может реализоваться.
. Взаимосвязи между событиями вводятся не с помощью непосредственных связей между ними, а путем описания тех ситуаций, при которых данное событие может реализоваться.
Условие (condition) 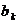 - предикат, являющийся логическим описанием ситуации, при которой некоторое событие
- предикат, являющийся логическим описанием ситуации, при которой некоторое событие 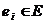 может произойти (реализоваться). Т.е. если предикат, соответствующий условию
может произойти (реализоваться). Т.е. если предикат, соответствующий условию 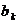 имеет значение “истина (“1”)”, то событие
имеет значение “истина (“1”)”, то событие 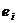 может произойти; если предикат, соответствующий условию
может произойти; если предикат, соответствующий условию 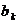 имеет значение “ложно (“0”)”, то событие
имеет значение “ложно (“0”)”, то событие 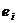 реализоваться не может. Через
реализоваться не может. Через  обозначается множество условий, которые связаны с событиями, принадлежащими множеству
обозначается множество условий, которые связаны с событиями, принадлежащими множеству 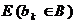 .
.
На практике, для того чтобы произошло событие 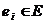 , часто может потребоваться выполнение не одного условия, а одновременно определенного сочетания условий.
, часто может потребоваться выполнение не одного условия, а одновременно определенного сочетания условий.
Предусловие (pre-condition) - логическое отношение “ 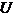 ” нескольких условий, при истинном значении которого некоторое событие
” нескольких условий, при истинном значении которого некоторое событие 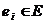 может реализоваться.
может реализоваться.
Пусть 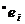 множество условий, входящих в предусловие события
множество условий, входящих в предусловие события 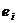
 . При реализации события
. При реализации события 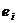 условия
условия 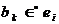 изменяются переходя из состояния “истинно” в состояние “ложно”. В то же время реализация события
изменяются переходя из состояния “истинно” в состояние “ложно”. В то же время реализация события 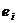 может оказывать влияние на какие-то условия, изменяя их значения.
может оказывать влияние на какие-то условия, изменяя их значения.
Постусловие (post-condition) - определенное сочетание нескольких условий 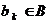 , на которые оказывает влияние реализация события
, на которые оказывает влияние реализация события 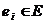 , делая их значения “истинными”.
, делая их значения “истинными”.
Пусть 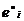 множество условий, входящих в предусловие события
множество условий, входящих в предусловие события 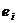
 . При реализации события
. При реализации события 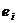 условия
условия  принимают значения “истина”. В частном случае условия
принимают значения “истина”. В частном случае условия 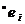 и
и 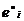 могут содержать только по одному условию или быть пустыми множествами.
могут содержать только по одному условию или быть пустыми множествами.
В отличие от синхронных математических моделей, в которых события явно привязаны к определенным моментам времени, заменим временные зависимости между событиями их причинно-следственными связями, которые устанавливают частичный порядок возникновения событий.
Причинно-следственная связь (pre/consequence condition) -непосредственная зависимость между событием 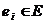 и условиями
и условиями 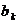 , принадлежащими его предусловию и постусловию
, принадлежащими его предусловию и постусловию 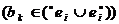 .
.
Введенные понятия позволяют определить состояние системы, заданной множеством событий 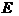 , множеством условий
, множеством условий  и совокупностью причинно - следственных связей, определенных для всех событий
и совокупностью причинно - следственных связей, определенных для всех событий 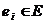 следующим образом.
следующим образом.
Состояние системы (state of system)  - совокупность значений истинности для каждого из условий
- совокупность значений истинности для каждого из условий 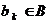 , в некоторый момент времени
, в некоторый момент времени  .
.
Пусть 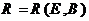 множество всех допустимых состояний системы
множество всех допустимых состояний системы 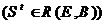 .
.
Основой изменения состояний системы является реализация тех или иных конкретных событий системы 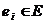 , которые переводят ее из текущего состояния
, которые переводят ее из текущего состояния  , в новое состояние
, в новое состояние 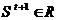 . Совокупность действий, возникающих как реализации событий при функционировании системы, образует процесс, порождаемый этой системой.
. Совокупность действий, возникающих как реализации событий при функционировании системы, образует процесс, порождаемый этой системой.
Правилами переходов  называются предположения, которые должны выполняться при изменении состояний системы в результате реализации отдельных событий.
называются предположения, которые должны выполняться при изменении состояний системы в результате реализации отдельных событий.
1. Отказ от временных зависимостей приводит к тому, что события 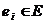 являются элементарными, т.е. являются неделимыми и происходят “мгновенно”, а изменения значений условий
являются элементарными, т.е. являются неделимыми и происходят “мгновенно”, а изменения значений условий 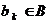 в предусловиях
в предусловиях  и постусловиях
и постусловиях  происходят одновременно, т.е. выполнение события
происходят одновременно, т.е. выполнение события  считается незримым актом.
считается незримым актом.
2. Реализация события 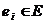 приводит к тому, что все условия
приводит к тому, что все условия  становятся “ложными”, а
становятся “ложными”, а  - “истинными”.
- “истинными”.
3. Считается, что события в системе не могут происходить одновременно, т.е. возможны только локальные изменения, связанные с реализацией одного конкретного события 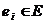 .
.
4. Каждое событие 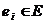 при определенных условиях может реализоваться хотя бы один раз.
при определенных условиях может реализоваться хотя бы один раз.
5. Каждое состояние системы  является достижимым из другого состояния за конечное число реализаций некоторой совокупности событий
является достижимым из другого состояния за конечное число реализаций некоторой совокупности событий  .
.
Если событие имеет длительность отличную от нуля, например,  -” задание в процессоре обрабатывается
-” задание в процессоре обрабатывается 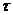 минут
минут  ”, и это существенно для функционирования системы, то событие
”, и это существенно для функционирования системы, то событие  представляется в виде двух событий
представляется в виде двух событий 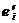 и
и  , которые происходят мгновенно:
, которые происходят мгновенно:
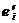 - “ начало обработки задания в процессоре”;
- “ начало обработки задания в процессоре”;
 - “ конец обработки задания в процессоре”;
- “ конец обработки задания в процессоре”;
и вновь вводимого условия 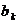 - “ обработка задания в процессоре в течение
- “ обработка задания в процессоре в течение 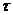 минут”, которое удовлетворяет следующим отношениям принадлежности:
минут”, которое удовлетворяет следующим отношениям принадлежности: 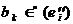 и
и  .
.




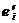
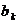

Если два события  с предусловиями
с предусловиями  и постусловиями
и постусловиями 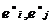 должны в системе реализовываться одновременно, то вместо них в систему вводится новое событие
должны в системе реализовываться одновременно, то вместо них в систему вводится новое событие 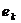 с предусловием
с предусловием 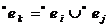 и постусловием
и постусловием 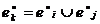 , которое интерпретируется как одновременная реализация событий
, которое интерпретируется как одновременная реализация событий 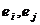 .
.







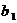

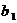
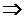









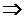

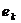



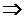








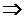


Таким образом, рассматриваемый класс сложных систем можно описать с помощью математической модели, представляющей из себя условно/событийную систему, которая моделирует изменение условий в результате реализации событий.
Условно/событийная система (condition/event system) – четверка  , где
, где 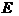 - конечное непустое множество событий;
- конечное непустое множество событий;  - конечное непустое множество условий;
- конечное непустое множество условий; 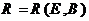 - множество достижимых состояний;
- множество достижимых состояний;  -отображение, описывающее совокупность правил перехода.
-отображение, описывающее совокупность правил перехода.
Введенное формализованное описание сложной системы как условно/событийной системы позволяет не только описывать ее структуру, но и анализировать динамические процессы, происходящие в ней.
Поведение условно/событийной системы (behavior od system) -последовательный переход системы из начального состояния 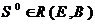 в любое достижимое состояние
в любое достижимое состояние 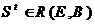 в результате реализации некоторой совокупности событий
в результате реализации некоторой совокупности событий  согласно правилам перехода
согласно правилам перехода  .
.
 Переход (transition)
Переход (transition)  - вершина двудольного графа, изображаемая черточкой “ ”.
- вершина двудольного графа, изображаемая черточкой “ ”.
Обозначим  конечное число переходов:
конечное число переходов:
 (имеется хотя бы один переход);
(имеется хотя бы один переход);
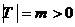 ,m - число рассматриваемых в системе событий (под систем или их действий).
,m - число рассматриваемых в системе событий (под систем или их действий).
Позиция (place)  - вершина двудольного графа, изображаемая кружком “ “, которая соответствует условию
- вершина двудольного графа, изображаемая кружком “ “, которая соответствует условию 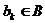 .
.
Обозначим через  - конечное множество позиций:
- конечное множество позиций:
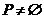 (имеется хотя бы одна позиция);
(имеется хотя бы одна позиция);
 число рассматриваемых в системе условий;
число рассматриваемых в системе условий;
 -конечное множество;
-конечное множество;
 - элемент множества
- элемент множества 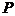 не может быть одновременно элементом множества
не может быть одновременно элементом множества  .
.
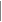 Причинно-следственные связи между событиями и условиями будем изображать в двудольном графе стрелочками “ Þ “:
Причинно-следственные связи между событиями и условиями будем изображать в двудольном графе стрелочками “ Þ “:
 – дуга, идущая от позиции
– дуга, идущая от позиции  к переходу
к переходу  :
:  Þ
Þ  , обозначает причинную связь между условием
, обозначает причинную связь между условием 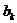 предусловия
предусловия 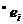 и событием
и событием  ;
;

 – дуга, идущая от перехода
– дуга, идущая от перехода  к позиции
к позиции  :
:  Þ
Þ  , обозначает следственную связь между событием
, обозначает следственную связь между событием  и условием
и условием 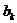 , принадлежащим постусловию
, принадлежащим постусловию  ;
;
– соединения между вершинами одного типа не допускаются, т.е. позиции соединяются только с переходами, а переходы - только с позициями;
– каждый элемент 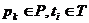 должен иметь как минимум одно соединение, т.е. в двудольном графе не может быть изолированных вершин.
должен иметь как минимум одно соединение, т.е. в двудольном графе не может быть изолированных вершин.
В некоторых случаях, чтобы событие  реализовалось (произошло), условие
реализовалось (произошло), условие 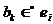 должно повториться несколько раз (например,
должно повториться несколько раз (например, 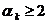 ).
).
Пучок дуг (bund of arches) - специальная дуга, которая изображается двойной стрелкой “  ” и помечается числом
” и помечается числом  , равным кратности дуги.
, равным кратности дуги.
Входная функция (функция предшествования; прямая функция инцинденций) - отображение  которое каждому переходу
которое каждому переходу 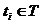 ставит в соответствие комплект входных позиций:
ставит в соответствие комплект входных позиций: 
Выходная функция (функция следования; обратная функция инцинденций) - отображение  которое каждому переходу
которое каждому переходу 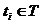 ставит в соответствие комплект выходных позиций:
ставит в соответствие комплект выходных позиций: 
Входная  и выходная
и выходная 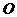 функции могут быть соответственно заданы с помощью матрицы прямых инцинденций
функции могут быть соответственно заданы с помощью матрицы прямых инцинденций 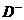 и матрицы обратных инцинденций
и матрицы обратных инцинденций 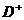 размерности
размерности  , в которых строки соответствуют позициям, а столбцы – переходам.
, в которых строки соответствуют позициям, а столбцы – переходам.
Сеть Петри(Petrinet) - четверка 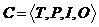 , задающая причинно - следственные связи в условно/событийной системе, где
, задающая причинно - следственные связи в условно/событийной системе, где  - конечное непустое множество переходов;
- конечное непустое множество переходов; 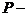 конечное непустое множество позиций;
конечное непустое множество позиций; 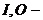 входные и выходные функции.
входные и выходные функции.
Таким образом, сеть Петри является графическим представлением структуры (статической топологии) моделируемой условно/событийной системы в виде двудольного графа с двумя видами вершин: вершин  (изображаемых кружками) и вершин
(изображаемых кружками) и вершин 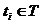 (изображаемых черточками). Эта абстрактная модель была предложена в 1962 г. немецким исследователем Карлом Адамом Петри для описания параллельных потоков информации в асинхронных системах.
(изображаемых черточками). Эта абстрактная модель была предложена в 1962 г. немецким исследователем Карлом Адамом Петри для описания параллельных потоков информации в асинхронных системах.
В зависимости от вида ориентированного графа, изображающего условно/событийную систему, можно указать следующие типы сетей Петри.
Связная сеть Петри - сеть Петри 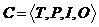 , двудольный ориентированный мультиграф которой позволяет пройти из любой вершины в любую другую вершину по пути вдоль и против дуг.
, двудольный ориентированный мультиграф которой позволяет пройти из любой вершины в любую другую вершину по пути вдоль и против дуг.







 |  |  |  | ||||

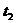





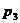

Сильно-связная сеть Петри - сеть Петри 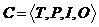 , двудольный ориентированый мультиграф которой позволяет из любой вершины пройти в другую только вдоль дуг.
, двудольный ориентированый мультиграф которой позволяет из любой вершины пройти в другую только вдоль дуг.
Емкость  й позиции - целое неотрицательное число
й позиции - целое неотрицательное число  , которое характеризует степень выполнения
, которое характеризует степень выполнения  го условия:
го условия:
– 0,  е условие не выполнено, ”ложно”;
е условие не выполнено, ”ложно”;
–  1,
1,  е условие выполнено, ”истинно”;
е условие выполнено, ”истинно”;
– 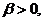
 е условие выполнено с
е условие выполнено с  -кратным запасом;
-кратным запасом;
– ( - целое положительное число).
- целое положительное число).
Маркер (taken) - символ в виде точки “ 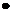 ”, который используется в соответствующих кружках (позициях) для обозначения емкости каждого из условий, то есть маркер является примитивным понятием сети Петри, подобным понятиям “переход” и “позиция”. Наличие маркера внутри кружка (позиция
”, который используется в соответствующих кружках (позициях) для обозначения емкости каждого из условий, то есть маркер является примитивным понятием сети Петри, подобным понятиям “переход” и “позиция”. Наличие маркера внутри кружка (позиция 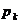 ), говорит о выполнении условия
), говорит о выполнении условия  (это событие “истинно”), а отсутствие маркера говорит о невыполнении условия
(это событие “истинно”), а отсутствие маркера говорит о невыполнении условия  (оно - ”ложно”).
(оно - ”ложно”).
Маркировка (разметка) сети Петри (marking) - отображение 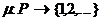 (множество натуральных чисел), с помощью которого всем позициям сети Петри приписываются определенные емкости
(множество натуральных чисел), с помощью которого всем позициям сети Петри приписываются определенные емкости 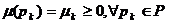 .
.
Маркировка сети Петри может быть задана с помощью 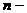 мерного вектора маркирования:
мерного вектора маркирования:
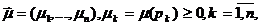
который полностью описывает текущее состояние  условно/событийной системы в некоторый момент времени
условно/событийной системы в некоторый момент времени  .
.
При 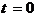 будем иметь начальную маркировку
будем иметь начальную маркировку 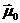 , которая задает исходное состояние системы
, которая задает исходное состояние системы  перед началом ее функционирования.
перед началом ее функционирования.
Маркированная сеть Петри 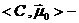 сеть Петри
сеть Петри 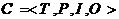 с заданной начальной маркировкой
с заданной начальной маркировкой 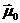 .
.
Динамическое поведение условно/событийной системы, описываемой с помощью сети Петри, можно определить следующим образом.
Функционирование (поведение, работа) сети Петри - последовательный процесс изменения количества и местоположения маркеров в позициях  маркированной сети Петри
маркированной сети Петри  при ее переходе из одного состояния в другое.”
при ее переходе из одного состояния в другое.”
Таким образом, представление реальной условно/событийной системы в виде маркированной сети Петри  является формальной и наглядной записью алгоритма ее функционирования. При этом невозможные события (события, в некоторых входных позициях которого отсутствуют маркеры) произойти (реализоваться) не могут.
является формальной и наглядной записью алгоритма ее функционирования. При этом невозможные события (события, в некоторых входных позициях которого отсутствуют маркеры) произойти (реализоваться) не могут.
Последовательность маркеров в сети Петри отражает динамику процесса, так как поток событий распространяется вдоль направления дуг ориентированного графа сети Петри. Хотя сеть Петри не содержит временных характеристик процессов в явном виде, она отражает определенное временное упорядочение событий, заданное отношениями типа: “раньше”, “позже”, “одновременно”, “независимо” и т. д. При этом функционирование сети Петри не указывает в какое время реализуется возможное событие, а только позволяет учесть реальную асинхронность и недетерминированность времени реализации событий.
Типы сетей Петри






