Непрерывно стохастические модели строятся для систем массового обслуживания (СМО). СМО – математические модели, которые используются при формализации процесса функционирования систем. В этих системах ключевым элементом является процесс обслуживания (процессы различной природы – экономические, природные). Общее для них – потоки заявок на обслуживание, и завершение обслуживания заявки происходит в случайные моменты времени (носят стохастический характер).
Для описания СМО используется 2 способа:
– аналитический – общая теория очередей;
– имитационный.
Базовым элементом СМО является прибор обслуживания, который имеет следующие компоненты:
Это можно изобразить в виде некоторого i -го прибора обслуживания Пi.
 |
1. Накопитель заявок Нi, в котором может находиться одновременно заявок;
2. 
, 
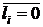, где -емкость i -го накопителя.
3. Канал обслуживания Ki.
Поток событий – последовательность событий, происходящих одно за другим в какие-то случайные моменты времени.
Однородный поток событий характеризуется только моментами поступления этих событий и задается последовательностью {tn}={0 £ t1 £ … £ tn £ …}, где tn – момент поступления n -го события – неотрицательное вещественное число.
Однородный поток событий также может быть задан в виде последовательности промежутков между n -м и (n-1)-м событиями { t n }, которая однозначно связана с последовательностью вызывающих моментов {tn}, где t n =tn – tn-1, n ³ 1, t0=0, т.е. t 1 =t1.
Поток неоднородных событий – последовательность {tn, fn}, где tn – вызывающие моменты; fn – набор признаков события.
Пусть имеется поток, в котором события разделены интервалами времени t 1, t 2,…, являющимися случайными величинами и интервалы t 1, t 2,… независимые между собой. Тогда поток событий называется потоком с ограниченнымпоследействием.
Ординарный поток событий – поток, если вероятность того, что на малый интервал времени D t, примыкающий к моменту времени t, попадает больше одного события P>1(t, D t), пренебрежительно мала по сравнению с вероятностью того, что на этот же интервал времени D t попадает ровно одно событие P1(t, D t), т.е. P1(t, D t)>>P>1(t, D t).
Если для любого интервала D t событие P0(t, D t)+P1(t, D t)+P>1(t, D t)=1 как сумма вероятностей событий, образующих полную группу и несовместных, то P0(t, D t)+P1(t, D t)» 1, P>1(t, D t)=0(D t), где 0(D t) – величина, порядок малости которой выше чем D t, т.е. 
Стационарный поток событий – поток, для которого вероятности появления того или иного числа событий на интервале времени t зависит только от длины этого участка и не зависит от того, где на оси времени взят этот участок.
Рассмотрим на оси времени ординарный поток событий, наступающих на интервале времени D t, примыкающем к моменту времени t. Тогда 0 × P0(t, D t)+1 × P1(t, D t)=P1(t, D t).
Тогда среднее число событий, наступающих на участке времени D t в единицу времени [P1(t, D t)]/ D t.
Интенсивность (плотность) ординарного потока событий –
.
Интенсивность может быть любой неотрицательной функцией времени, имеющей размерность, обратную размерности времени.
Для стационарного потока его интенсивность не зависит от времени и представляет собой постоянное значение, равное среднему числу событий, наступающих в единицу времени l (t)= l =const.
На каждый элемент прибора обслуживания поступают заявки. Подмножество входных заявок Wi, задаваемое как интервалы времени между появлениями заявок, образует множество W неуправляемых переменных и Ui – поток обслуживания (интервалы времени между началом и концом обслуживания заявок). Заявки, обслуженные каналом ki и заявки, покинувшие канал ni , образуют выходной поток yi, которые описывается как моменты времени выхода заявок из прибора. Процесс функционирования прибора Пi представляется как процесс изменения состояния его элементов во времени. Переход в новое состояние Пi означает либо изменение количества заявок, которые в нем находятся, либо изменение выходного потока yi, то есть вектор состояния прибора имеет вид
(t) = (
, 
), (10)
где 
– состояние накопителя (0 – свободен, 1– занят),
– состояние канала (0, 1, 2,...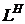 
).
При Zik=Lik накопитель полностью заполнен, где LiH – емкость накопителя Hi.
В зависимости от количества каналов различают многоканальные и одноканальные приборы.
Параллельное соединение каналов – многоканальная Q -схема.
Последовательное соединение приборов и их элементов образуют многофазный прибор обслуживания.
Различают разомкнутые и замкнутые Q -схемы.
В разомкнутых Q -схемах выходной поток заявок не может снова поступать на какой-то элемент Q -схемы (система без обратной связи).
В замкнутых Q -схемах часть выходного потока может поступать на какие-либо элементы системы.
Различают:
– Q -схемы с ожиданием 
, если емкость накопителя не ограничена, и очередь заявок не ограничивается.
– Q -схемы с потерями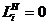 
, когда накопитель в системе отсутствует, а имеется канал обслуживания.
Для описания функционирования системы необходимо задать алгоритм ее функционирования, который определяет набор правил поведения заявок в различных неоднозначных ситуациях.
В зависимости от места возникновения таких ситуаций различают алгоритмы ожидания заявок в накопителе Нi и обслуживания заявок каналом Кi каждого элементарного обслуживающего прибора Пi Q– схемы.
У каждого потока заявок может быть определены приоритеты. Различают статические (назначаются заранее и не зависят от состояния Q -схемы) и динамические (возникают в результате функционирования Q -схемы в зависимости от возникающих ситуаций) приоритеты.
Выделяют относительные (означает, что при поступлении заявки с более высоким приоритетом, эта заявка ожидает конца обслуживания предыдущей и затем поступает на обслуживание вне очереди) и абсолютные (означает, что заявка с таким приоритетом прерывает процесс обслуживания предыдущей заявки и обслуживается в канале. Предыдущая заявка может покинуть систему или помещена в какой-либо накопитель) приоритеты.
Таким образом, различают следующие приборы обслуживания:
– одноканальные и многоканальные;
– однофазные и многофазные;
– с повторными вызовами и без них;
– с различными потоками заявок;
– с различными законами распределения.
Для обозначения различных очередей используют латинские буквы, разделенные вертикальными или наклонными чертами, которые обозначают набор условий:
А ½ В ½ m ½ n ½ C,
где А – указывает на распределение интервалов между последовательными моментами поступления заявок на обслуживание;
В – закон распределения длительности заявок на обслуживание;
m – канальность системы (число обслуживающих каналов);
n – количество мест в очереди (емкость в накопителе);
С – дисциплина очереди (LIFO, FIFO).
Буквой М обозначается простейший поток заявок с показательным распределением. Е – поток Эрланга (Пуассоновское распределение). 1 Эрланг – одна транзакция в единицу времени.
