Имеется телефонная станция (центр), в которой m каналов (m может быть как конечной, так и бесконечной величиной). Вызовы поступают на станцию в моменты t1,…, tn,…(0<t1 <…<tn < ¥).
Сделаем предположения относительно управления вызовами, поступающими на станции.
1. Связь реализуется, если поступающий вызов находит свободный канал.
2. Поступающий вызов может занять любой свободный канал, то есть группа каналов является полнодоступной.
3. После окончания разговора занятый канал немедленно становится доступным для нового вызова.
4. Если поступающий вызов найдет все каналы занятыми, то каждый новый вызов поступает в очередь и ожидает, пока канал не освободится. Все каналы имеют общую очередь.
Рассмотрим характеристику процесса обслуживания. В системе имеется m обслуживающих приборов. Рассмотрим функцию распределения интервалов между поступлениями вызовов и длительностью обслуживания (разговоров).
Пусть интервалы между поступлениями tn образуют последовательность рекуррентных событий, то есть интервалы между поступлениями.
, (n=1,2,…) – одинаково распределенные, независимые положительные случайные величины, и A(t) – их общая функция распределения.
Пусть 
- средняя длительность интервала между поступлениями.
- длительность разговора вызова, поступившего в момент tn. Пусть (n=1,2,…) одинаково распределенные независимые случайные величины, независящие от процесса {tn}.
Пусть функция распределения длительностей разговора является показательной:
(35)
Одной из основных задач телефонии является определение вероятности Px(t) того, что из группы в m-каналов в момент t занято х. Особое внимание уделяется исследованию предельных вероятностей 
Пример. Рассмотрим Марковский процесс на телефонной станции с бесконечным числом каналов.
Пусть случайная величина x(t) – число занятых каналов в момент t и 
. Так как x может принимать значения 0,1,…, то процесс 
является Марковским со счетным множеством состояний. Система находится в состоянии х, если занято х каналов. В силу предположений о моментах поступления и длительностей разговоров,
1) вероятность того, что в интервале (t, t+Dt) вызов поступит на станцию, равна lDt +0(Dt), l>0;
2) если в момент t занято х каналов, что один из них освободится в интервале (t, t+Dt), равна хmDt +0(Dt), m>0;
3) если в момент t занято х каналов, то вероятность того, что ни один из каналов не освободится и вызов не поступит на станцию в интервале (t, t+Dt)=1-(l+хm)Dt +0(Dt);
4) вероятность осуществления любых других событий в интервале (t, t+Dt)=0(Dt);
Поэтому в интервале (t, t+Dt) с точностью до величин вероятностей порядка 0(Dt) возможны лишь следующие переходы: (х®х+1), (х®х-1), (х®х).
Такой Марковский процесс является процессом рождения и гибели с интенсивностями рождения и гибели 
. Тогда
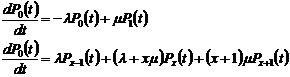. (36)
