Задачи принятия решений в условиях неопределенности встречаются в жизни на каждом шагу, и имитационное моделирование является основным способом получения обоснованного решения в этих условиях. В качестве входных данных имитационной модели в таких задачах используются случайные величины, поэтому и выходные данные прогона имитационной модели будут случайными величинами.
Конечно, каждый прогон имитационной модели должен выполняться только при конкретных значениях параметров. Например, для оценки будущей прибыли на автозаправочной станции нужно задать конкретные значения цены на топливо и эксплуатационные расходы в будущем году. Эти значения могут быть только какими-либо конкретными реализациями случайных величин, поэтому и результаты, полученные после прогона модели с этими
случайно выбранными входными значениями, будут тоже случайными значениями. Для получения разумной характеризации выходных случайных величин нужно многократно выполнять имитационную модель, выбирая различные реализации случайных входных параметров (рис. 10.4).

Вектор входных случайных значений следует, конечно, выбирать в соответствии с их вероятностными распределениями, известными или предполагаемыми. Очевидно, что любой результирующий показатель исследуемой модели в этом случае тоже будет величиной случайной с некоторым законом распределения, характеристики которого можно определить в результате многократного выполнения имитационного эксперимента (рис. 10.5).
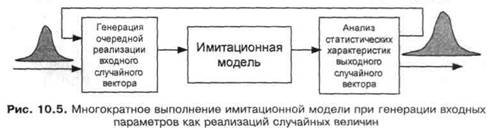
Оба блока — блок генерации случайных реализаций входных величин и блок анализа статистических характеристик случайных реализаций выходных характеристик модели — можно включить в имитационную модель. Тогда ее можно считать просто преобразователем случайных величин (рис. 10.6).

В AnyLogic включено 37 генераторов случайных величин с наиболее часто встречающимися вероятностными распределениями: равномерным, экспоненциальным, Бернулли, биномиальным и т. д. Все их можно найти в Руко водстве пользователя AnyLogic.
Все классы вероятностных распределений унаследованы от класса Distr. Они называются DistrExponential, DistrChi, DistrNormal И Т. Д. Класс Distr имеет только один абстрактный метод get (), возвращающий случайное значение, сгенерированное по этому закону распределения. Пользователь может определить свое вероятностное распределение, для чего нужно создать свой класс распределения и унаследовать его от базового класса Distr. Методы классов распределений подробно описаны в Справочнике классов AnyLogic.
У класса Activeobject есть унаследованные от класса Func статические методы, которые идентичны описанным ранее методам классов вероятностных распределений. Поэтому в активном объекте достаточно просто вызвать метод, например exponential(0.6) или uniform(-l, 1), который вернет соответствующее случайное значение.
Примером модели, на входе которой генерируется случайная величина и случайные же величины получаются на выходе, является модель операционного зала банка, рассматривавшаяся в главе 6. Другая модель этого типа — знакомая нам модель ErlangProblem (глава 9). На ее входе генерируются случайные интервалы, через которые, в соответствии с предположением, будут поступать телефонные вызовы на автоматическую телефонную станцию. Случайными здесь являются также генерирующиеся автоматически времена обслуживания каждого телефонного вызова. Выходом этой модели является величина прибыли Benefit, которая тоже является случайной величиной.
AnyLogic включает средства, позволяющие выполнять анализ случайных величин и визуализировать их распределения. Анализ случайной величины в AnyLogic легко выполняется, если эта величина представлена как "набор данных". Для наборов данных автоматически подсчитываются их стандартные характеристики: количество реализаций, среднее, минимальное и максимальное значения, дисперсия, среднеквадратичное отклонение и доверительный интервал для среднего значения. Мы рассматривали использование наборов данных в главе 6.
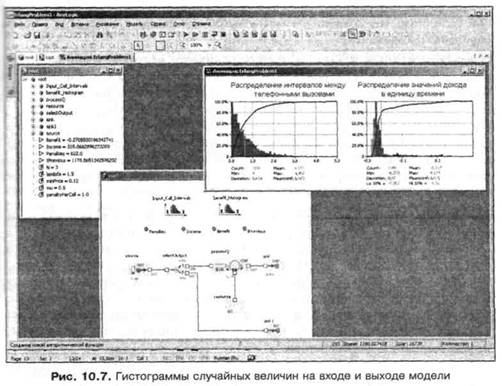
Для визуализации случайной величины наиболее употребительным средством является гистограмма. Гистограмма представляет собой совокупность смежных прямоугольников, построенных на одной прямой; площадь каждого из прямоугольников пропорциональна частоте попадания значения случайной величины в интервал, на котором построен данный прямоугольник. AnyLogic содержит встроенные средства для быстрого построения гистограмм случайных величин. Рисунок 10.7. показывает гистограммы входной
случайной величины (интервалов времени между приходящими в систему телефонными вызовами) и выходной случайной величины (дохода) для модели предоставления сервиса автоматической телефонной связи. Модель Erlangproblem3, в которую включены эти гистограммы, находится в папке ModelExamples\Part III. Рассмотрим, как строить эти гистограммы.
Библиотека графики для бизнеса (Business Graphics Library) содержит классы Histogram simple и Histogram Smart для построения гистограмм. Рассмотрим первый из них.
Для построения гистограммы распределения интервалов входных звонков, сначала следует ввести в модель новую анимацию, и в поле анимации ввести прямоугольник, который по умолчанию получит имя rectangle. Гистограмма будет отображаться при работе модели в пределах этого прямоугольника. В поле редактора модели введем методом drug-and-drop один экземпляр класса Histogram simple и поместим его в любое место поля редактора. В окне его свойств можно установить имя (назовем этот экземпляр input_call_intervals) и другие параметры. В поле значений параметра placeholder этого объекта должно стоять имя того графического объекта,
в пределах которого будет строиться гистограмма. С помощью выпадающего меню вставим в это поле имя animation.rectangle. Для параметра updateMode (метод обновления) следует в выпадающем меню выбрать один из трех возможных вариантов добавления значений случайной величинины в накопитель, связанный с этой гистограммой. Выберем метод обновления MANUAL - USE add FUNCTION. Это означает, что каждый раз, когда будет нужно добавить очередное значение реализации интересующей нас случай ной величины, мы должны вызывать метод add данного объекта (с именам
Input_Call_Intervals).
Параметры Minimum и Maximum задают нижнюю и верхнюю границы интер-вала, на котором будет строиться гистограмма. Определим значение Maximum числом 5. Параметр Numberofintervals определяет число интервалов (прямоугольников) гистограммы. Выберем число 50. Параметр RelativeBarwidth устанавливает относительную ширину прямоугольника на каждом из интервалов. Выберем для него значение 1. На гистограмме будет также показы ваться интегральная функция распределения (Cumulative Distribution Function, CDF). Выберем толщину линии представления графика этой функции 2. Остальные параметры оставим без изменения.
Рассмотрим теперь, как добавлять значения генерируемой случайной величины — интервала между последовательными телефонными вызовами. Телефонные вызовы моделируются блоком source модели. Фактически, эти интервалы определены функцией exponential (lambda), которая является зачением динамического параметра interarrivaiTime, однако напрямую в данном блоке значения этой случайной величины получить нельзя. Используем следующий прием. Введем в модель переменную tPrevious с начальным значением 0 и каждый раз, как этим блоком будет генерироваться заявка, выполним два оператора:
lnput_Call_lntervals.add(getTime()-tPrevious); // добавляем значение tPrevious = getTime(); // запоминаем момент текущего звонка
Эти операторы должны быть помещены в поле параметра onExit блока
source.
Вторая гистограмма строится полностью аналогичным образом. Исключение составляет только значение параметра UpdateMode (метод обновления). Эта гистограмма должна показывать распределение значений случайной величины Benefit, для которой не определены явно моменты ее изменения: она задана формулой, связывающей несколько случайных величин. Поэтому удобно определить updateMode этой гистограммы как AUTO - ADD Data EVERY TimeStep. При этом нужно указать временной шаг (оставим его заданным 1 по умолчанию), а также имя данного (у нас это Benefit), текущее значение которого принимается за новую реализацию случайной величины каждый раз при наступлении этого временного шага.
Принятие решений






