Пусть проведена неподвижная замкнутая поверхность S в потоке жидкости, обтекающем неподвижное твердое тело M (рис. 1- 8). Жидкий объем, заключенный внутри S, имеет своей наружной границей поверхность S, а внутренней границей – поверхность твердого тела M. Через бесконечно малый промежуток времени dt, жидкий объем переместится в положение S', которое мы получим, отложив от каждого элемента поверхности S вектор 
.
В случае установившегося движения уравнение сохранения количества движения будет иметь вид:
где 
и 
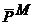- главные векторы давлений, приложенных к S и M.
Закон сохранения моментов количеств движений приводит к уравнению:
где 
и 
главные моменты сил гидродинамических давлений к поверхностям S и M; 
- радиус-вектор элементарной частицы dm /
Конечно-разностные формы решения уравнений движения жидкости
Разностной схемой решения краевой задачи называют совокупность разностных уравнений, заменяющих данные дифференциальные уравнения, граничные и начальные условия. Одним из способов аппроксимации дифференциальных уравнений разностными заключается в следующем. При помощи системы пересекающихся линий в рассматриваемой области вводится разностная сетка – совокупность узлов (точек пересечения линий), в которых отыскивается приближенное решение. Затем выбирается сеточная конфигурация – группа узлов, которые привлекаются для локальной аппроксимации дифференциальных уравнений. После этого каждая из производных, входящих в уравнение, заменяется отношением разности значений функции в узлах выбранной конфигурации к разности соответствующих значений аргумента.
Например, рассмотрим т.н. задачу Коши для переноса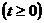 
Введем в плоскости (x,t) сетку из параллельных прямых
и будем конструировать разностную схему при помощи трехточечной конфигурации (рис. 1 - 9).
Занумеруем узлы сетки парами целых чисел (k, n) и примем обозначение f(kΔx, nΔt)= 
. Для замены производных в узле (k,n) воспользуемся разностными отношениями
Коэффициент a(x, t) будем брать в узле (k, n). В результате замены получаем разностную схему:
Мы познакомились в первом приближении с порядком составления разностных схем. В практике решения различных задач используется множество разностных схем и способов их решения. Эти задачи решают специалисты механики (теоретики) и математики. Практики - строители должны уметь находить уже реализованные на ЭВМ нужные решения и применять их в своей практической деятельности.
2.2. УРАВНЕНИЕ Д. БЕРНУЛЛИ ДЛЯ ЭЛЕМЕНТАРНОЙ СТРУЙКИ
ИДЕАЛЬНОЙ ЖИДКОСТИ
