Частоту вращения
Предположим, что имеется характеристика нагнетателя при частоте вращения n1, а двигатель этого насоса работает при частоте вращения n2, отличной от n1. Для того чтобы судить об эксплуатационных свойствах нагнетателя, необходимо иметь его характеристику при той частоте вращения n2, при которой он фактически будет работать.
Эту характеристику можно получить путем пересчета имеющейся характеристики на новую частоту вращения п2 по формулам. Для этого задаются рядом значений подач Q1 и по имеющейся характеристике нагнетателя находят соответствующие им напор Н1, мощность N1 и КПД η1 (рис. 4.1).
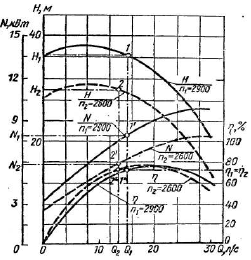
Рис. 4.1. Пересчет характеристики нагнетателя на другую частоту вращения
Подставив найденные для частот вращения nx величины Q1, H1 N1 и η1 в уравнения (4.4), получают значения подачи Q2, напора H2, мощности N2 и КПД η2, которые представляют собой координаты точек характеристики нагнетателя при частоте вращения n2. По этим координатам строят на характеристике ряд точек, соединив которые плавными кривыми, получают искомую характеристику нагнетателя при частоте вращения n2.
Найдем в координатах Q - H геометрическое место точек режимов, подобных режиму, который определяется точкой 1 (рис. 4.2).
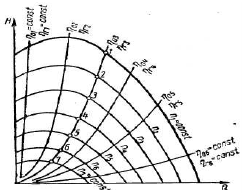
Рис. 4.2. Кривые подобных режимов
Для этого, подставив координаты Q1 и Н1 точки 1 в уравнения (4.4), определим напор и подачу при различных значениях частоты вращения. В результате найдем ряд точек: 2, 3, 4,..., соединив которые плавной линией, получим кривую подобных режимов работы нагнетателя. Покажем, что эта кривая представляет квадратичную параболу с вершиной в начале координат. Для этого подставим в уравнение (4.4) значения п1/п2

Следовательно, уравнение кривой подобных режимов имеет вид
H = s·Q2
Для подобных режимов гидравлический и объемный КПД с достаточной степенью точности можно считать одинаковыми, так как с увеличением частоты вращения роль потерь на трение уменьшается.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
Задача 1.
При испытании на воде модели насадка, выходной диаметр которого dм= 30 мм, под статическим напоромHм = 50 м получены расход Qм = 18 л/с и средняя скорость в сжатом сечении струи wм = 30 м/с.

Каков должен быть выходной диаметр насадка в натуре и под каким напором Н он должен работать на воде, чтобы получить Q = 100 л/с и
wм = 60 м/с?
Считать, что испытания модели произведены в зоне турбулентной автомодельности, поэтому коэффициенты истечения для модели и натуры одинаковы.
Варианты:
| № | dм | Hм | Qм | wм |
| 1 | 31 | 51 | 19 | 31 |
| 2 | 32 | 52 | 20 | 32 |
| 3 | 33 | 53 | 21 | 33 |
| n |
Решение
Расход через отверстие равен Q=S μ 2g H = Sw;

Коэффициент расхода

Тогда при скорости струи w = 60 м/с напор составит

Выходной диаметр насадка
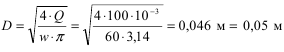
Задача 2.
Диафрагма размерами d = 100 м и D = 200 мм, предназначенная для измерения расхода воздуха, тарируется путем испытания на воде.

В результате испытаний получено, что минимальный расход воды, начиная с которого коэффициент расхода диафрагмы остается постоянным, Qmin = 16 л/с, и при этом показание ртутного дифманометра, измеряющего перепад давлений на диафрагме, hрт = 45 мм.
1. Определить Qmin при работе диафрагмы на воздухе.
2. Найти соответствующее этому расходу воздуха показание водяного дифманометраhв, присоединенного к диафрагме в тех же точках.
Кинематическая вязкость воды ν = 10-2Ст, динамическая вязкость
воздуха μ = 1,82·10-4 П (1Пуаз = 0,1 Па·с) и его плотность ρ = 1,166 кг/м3.
Указание. Значениям расхода Qminпри работе диафрагмы на различных жидкостях соответствует одинаковое число Рейнольдса, представляющее границу зоны турбулентной автомодельности.
Решение

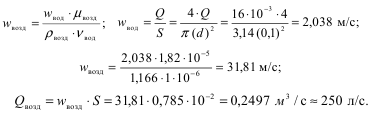
Для подобных потоков можно принять

Тогда

Задача 3.
Тонкая пластина длиной l0 = 2 м и шириной а = 1,5 м обтекается продольным потоком воздуха. Скорость и температура набегающего потока равны соответственно wo=3 м/с;

t0 = 20 °C. Температура поверхности пластины равна tс = 90 °С. Определить средний по длине коэффициент теплоотдачи и количество тепла, отдаваемое пластиной воздуху.
Решение
Для воздуха при t0 ≈ 20 °С и ν = 15,06 · 10 - 6 м2/с; λ=2,23 · 10 - 2 ккал/(м чград); Рr = 0,703, откуда

В этих условиях средняя по длине теплоотдача может быть рассчитана по формуле

Где

и физические параметры выбираются при температуре t0. В рассматриваемомслучае

икоэффициенттеплоотдачи
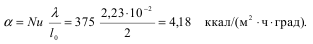
Количество передаваемого тепла с обеих сторон пластины

Задача 4.
Вычислить для условий задачи № 3 толщину гидродинамического пограничного слоя и значения местных коэффициентов теплоотдачи на расстояниях от передней кромки пластины х = 0,1l0; х = 0,2l0; x = 0,5l0 и х = l0. Построить график зависимости толщины гидродинамического пограничного слоя δл и коэффициента теплоотдачи от расстояния х/l0.
Решение
По условиям задачи № 3 теплоотдача происходит в условиях ламинарного пограничного слоя, толщина которого и местный коэффициент теплоотдачи на расстоянии х от передней кромки пластины определяются по формулам

Где

На расстоянии x = 0,1·l0:


Аналогичным образом рассчитывается δлам и α при х = 0,2·l0; х = 0,5·l0 и x=l0. Результаты расчетов приведены на рисунке.

Тесты для проверки знаний




