В основе этого метода лежит так называемая Пи-теорема, или теорема Бэкингема, которая заключается в следующем: функциональная зависимость между n физическими размерными величинами всегда может быть преобразована в уравнение, содержащее m безразмерных комбинаций тех же физических величин (так называемых чисел π), причем m всегда меньше n. Разность n-m=z представляет собой число первичных (основных) единиц, например в механике и гидромеханике – единицы длины, времени и массы, т. е. z = 3, а в теплотехнике к перечисленным единицам добавляется еще температура, следовательно z = 4.
Был рассмотрен такой случай, когда уравнение Бернулли, записанное в размерных величинах, связывало между собой пять размерных переменных: v1,p1,v2, p2 и hM. А после приведения этого уравнения к безразмерному виду в нем остались лишь две безразмерные переменные: число Эйлера Еu и коэффициент потерь ζ.
Рассмотрим получение формулы Дарси – Вейсбаха.
Очевидно, что на потерю давления на трение в трубе Ртр = hтрρgвлияют (или могут влиять) следующие факторы: длина l и диаметр d трубы, средняя скорость течения v, свойства жидкости ρ и μ и средняя высота бугорков шероховатости Δ на стенках трубы.
Запишем интересующую функцию в виде

Число переменных п = 7, следовательно, в соответствии с Пи-теоремой т = п-z = 7-3 = 4 и вместо предыдущего можем записать

где π, π1, π2 и π3 - безразмерные комплексы, вид которых найдем следующим путем.
Из числа n переменных выберем три с независимыми размерностями, включающими в себя три основные единицы (длины L, времени Т и массы М), например d, v и ρ; их размерности в системе LTM таковы:

Выразим числа π, π1, π2 и π3делением на выбранные три переменные в некоторых степенях х, у и z (с соответствующими индексами) остальных четырех переменных, а именно: pmp, l, μ и Δ, которые имеют следующие размерности:

Таким образом, будем иметь

Найдем все 12 показателей степеней из условия безразмерностивсех чисел π, т. е. сравнением размерностей при L, Т и М во всех четырех выражениях, а именно: показатели степени при L:

показатели степени при Т:

показатели степени при М:

Решая совместно полученные уравнения, получаем:
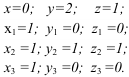
Таким образом, теперь мы можем записать

или, учитывая пропорциональность междуртр и l/d и выражение числа Рейнольдса, находим:

Обозначив функцию ϕ1 через λT, окончательно получим:

Где

Таким образом, получили формулу Дарси-Вейсбаха, а также информацию о том, какими факторами определяется коэффициент Дарси λT.






