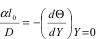На рисунке показана поверхность твердого тела, омываемая не-сжимаемой жидкостью, температура и скорость которой вдали от тела постоянны и равны соответственно t0 и w0.
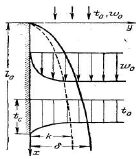
К постановке краевой задачи конвективного теплообмена
Размер тела l о задан.
Температура поверхности тела равна tc. Для определенности примем, что tc>to. Будем полагать, что физические параметры жидкости постоянны (учтем только подъемную силу, возникающую в результате зависимости плотности от температуры). Теплота трения не учитывается.Рассматриваемый процесс является стационарным. Расположим оси координат так, как показано на рисунке. Для простоты примем, что ось Оу нормальна к поверхности тела, а ось Ох направлена вдоль тела и вертикальна.
При этом gx = g, а проекции вектора сил тяжести (или подъемной силы) на оси Оу и Оz будут равны нулю (gy=gz = 0). Размер тела вдоль оси Оz намного больше lо.
При принятых условиях поля температур и скоростей можно описать дифференциальными уравнениями в приближении пограничного слоя. Учтем дополнительно подъемную силу ρ·g·β·V, считая ее соизмеримой с вязкостным членом μ{d2wx/dy2). Введем также обозначение θ= t – t0, где t0 – температура жидкости (заметим, что dt= dθ, так как t0 = const).
Уравнение энергии
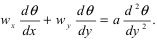
Уравнение движения

Уравнение сплошности

Напишем граничные условия
1) Вдали от тела (у = ∞) θx = θy = 0; wx= w0; wy= 0.
2) На поверхности тела (у = 0, 0<= x <=l0, - ∞ < z < +∞)
θ = θc = tc — t0 = const; wx = wy= wz = 0.
В уравнениях и условиях однозначности можно различить три вида величин:
независимые переменные – это координаты х, у;
зависимые переменные – это θ, wx и wy, они однозначно определяются значениями независимых переменных, если заданы величины, входящие в условия однозначности;
постоянные величины – это w0, t0,lо, θс, v, a, gβ и др., они задаются условиями однозначности и для определенной задачи являются постоянными, не зависящими от других переменных, от задачи к задаче они могут меняться. Постоянными эти величины называют потому, что они не являются функцией независимых переменных.
Величины, содержащиеся в уравнениях и условиях однозначности, можно сгруппировать в комплексы. Число безразмерных комплексов будет меньше числа размерных величин.
Для приведения к безразмерному виду выберем масштабы приведения. В качестве масштабов удобно принять постоянные величины, входящие в условия однозначности. Для линейных величин выберем какой-либо характерный размер, например длину поверхности теплообмена lо, для скорости w0, для температуры θс.
Обозначим безразмерные величины
X=x/l0, Y=y/l0, Wx=wx /w0, Wy=wy/w0, Θ= θ/θc
Тогда x = l0 ·Х, y = l0 ·Y, wx = Wx w0, wy= w0Wy, θ= θcΘ. (3.1)
Подставим в уравнения значения величин согласно равенствам (3.1). Преобразуем уравнение энергии

В результате подстановки равенств после умножения левой и правой частей уравнения энергии на l0 2 /a будем иметь

Аналогично преобразуем и уравнение движения. После подстановки равенства (3.1) в уравнение движения умножим его на l2o/(v ·w0).
В результате получим

Сделаем следующее преобразование комплекса, входящего в последнее уравнение:
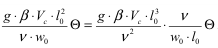
Учитывая эти преобразования, окончательно получаем:

После преобразования уравнения сплошности получим
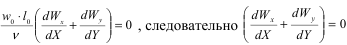
Приводя к безразмерному виду граничные условия, получаем:
1) Вдали от тела (У=∞) Θ=0, Wx=1, Wy=0. (3.2)
2) На поверхности тела (У=0, 0<= x < =1). (3.3)
Θ=Θc=1, Wx= Wy=0.
Из условий (3.2) и (3.3) следует, что, несмотря на то что величины и другие, входящие в размерные граничные условия могут иметь различные числовые значения, каждая из безразмерных величин θc, θ0 и др. имеет в рассматриваемом случае вполне конкретное числовое значение.
При известном температурном поле коэффициент теплоотдачи может быть определен по уравнению

Приводя к записи в безразмерных переменных α ⋅l0/λ,получаем