Необходимой предпосылкой теории подобия будет математическое описание изучаемого процесса в виде дифференциальных (или интегродифференциальных) уравнений и условий однозначности.
Из математической формулировки задачи следует перечень существенных для рассматриваемого процесса физических величин. Если перечень установлен, то числа подобия могут быть выявлены методом анализа размерностей.
Иногда список размерных величин устанавливают интуитивно, без строгой формулировки краевой задачи. В этом случае возможны ошибки. Напомним, что в основе метода анализа размерностей лежит Пи-теорема, которая гласит:
Физическое уравнение, содержащее n> 2 размерных величин, из которых к>1 величин имеют независимую размерность, после приведения к безразмерному виду будет содержать n-k безразмерных величин.
Можно различать два вида физических величин: первичные (основные) и вторичные (производные).
Первичные величины характеризуют какое-либо физическое явление непосредственно, без связи с другими величинами. Вторичными считаются величины, которые выражаются через первичные согласно определениям или физическим законам. Так, например, если длина и время – первичные величины, т. е. если длину нельзя выразить через время (и наоборот), то скорость, представляющая собой по определению отношение длины ко времени, является вторичной, производной величиной.
Выбор первичных величин, вообще говоря, произволен. В системе СИ за первичные выбраны длина L, масса М, время T, температура θ, сила тока I, сила света J. При выборе первичных величин большое значение имеет вопрос об удобстве их применения.
Символическое выражение производной величины через основные (первичные) называется размерностью. О размерности можно говорить только применительно к определенной системе первичных величин. Размерность можно представить в виде степенной формулы. Применительно к системе СИ формула размерности имеет вид
[ϕ]= Ln1⋅ M n2⋅Tn3⋅θn4⋅ In5⋅ Jn6 (3.6)
где [ϕ]– производная единица измерения; n – действительные числа. Размерность вторичной величины относительно данной первичной i может быть охарактеризована значением показателя степени n при этой первичной величине. Поэтому безразмерные числа часто называют величинами с нулевой размерностью, так как для них все показатели степени в формуле размерности равны нулю. Согласно формуле (3.6) размерность первичной величины можно принять равной единице (берется относительно себя).
Выбор единиц измерения первичных величин (основных единиц измерения) произволен и определяется вопросами удобства их использования.
Выбор перечня первичных величин и их единиц измерения является необходимым и основным шагом на пути создания системы единиц измерения.
Рассмотрим пример использования метода размерностей. Оп-ределим безразмерные переменные, соответствующие математической формулировке задачи. Из этой задачи следует, что

В списке величин, существенных для рассматриваемого процесса, представлено девять переменных (n = 9). В рассматриваемом нами примере использованы три первичные величины системы единиц измерения СИ: длина, время, температура (k = 3).
Пользуясь возможностью произвольного выбора основных единиц измерения, разделим переменные, входящие в уравнение, на две группы: на величины с независимой размерностью (основные) и на величины с зависимой размерностью (производные). Мы как бы создаем новую систему единиц измерения (специально для рассматриваемой задачи). Первый шаг на этом пути – выбор перечня первичных величин (величин с независимой размерностью).
За величины с независимой размерностью выберем постоянные
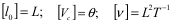
Размерность остальных величин выразим через них согласно формуле размерности
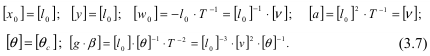
Назначим единицы измерения величин с независимой размерностью. За основные единицы измерения в данном случае удобно выбрать числовые значения постоянных l0, Θс и v, заданные в условиях однозначности. Новые числовые значения физических величин X, Θ и др. получают путем сравнения с новым стандартом, т. е. X=x/lO, Θ= θ/θcи т.д. Физический процесс не зависит от выбора единиц измерения, поэтому уравнение (3.7) должно сохранить свою структуру при различных значениях масштабов пересчета. В новых числовых значениях переменных уравнение (3.7) может быть записано следующим образом:
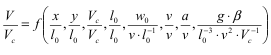
Здесь все величины-комплексы являются безразмерными. Величины, равные единице, могут быть выведены из-под знака функции.
Используем обозначения чисел подобия

При переходе к безразмерным величинам число переменных формально сократилось от девяти до шести. Аналогичный результат был получен с помощью метода масштабных преобразований.






