Теория подобия имеет большое значение при проектировании и экспериментальном исследовании лопастных нагнетателей, к которым относятся лопастные насосы и вентиляторы. Теория подобия дает возможность по известной характеристике одного нагнетателя (модельного) получить характеристику другого, если проточные полости обоих нагнетателей геометрически подобны, а также пересчитать характеристику нагнетателя с одной частоты вращения на другую.
Это облегчает экспериментальное исследование лопастного нагнетателя, давая возможность получить характеристику мощного натурного нагнетателя путем испытания его уменьшенной модели или же испытывать натурный нагнетатель на частоте вращения, отличающейся от той частоты вращения, на которой он эксплуатируется.
Применение формул подобия будет справедливо при соблюдении следующих условий:
1. Геометрическое подобие проточных полостей нагнетателя, включающее также подобие шероховатостей поверхности стенок внутренних каналов, зазоров в щелевых уплотнениях и толщин лопаток рабочего колеса.
2. Кинематическое подобие на границах потоков. Границами потока являются, в частности, его сечение у входа в нагнетатель и движущиеся лопатки колеса. Для выполнения условий кинематического подобия на границах потоков необходимо, чтобы средняя скорость жидкости vвх у входа в нагнетатель была пропорциональна окружной скорости рабочего колеса и:
Скорость абсолютного движения v (абсолютная скорость) равна геометрической сумме скорости w жидкости относительно рабочего колеса (относительной скорости) и окружной скорости u рабочего колеса (переносной скорости), т. е. v=w+u).
vвх ~u=π ·D ·n/60~ n ·L,
где n- частота вращения рабочего колеса; L - характерный размер насоса, например диаметр колеса.
Подача нагнетателя равна произведению скорости vвх на площадь нормального сечения потока у входа в насос, которая пропорциональна линейному размеру L во второй степени. Отсюда
Q ~νвхL2 ~ n ·L3 (4.1)
или

где индексом 1 обозначены величины для первого нагнетателя, индексом 2 - для второго, геометрически подобного первому.
3. Динамическое подобие потоков. Динамическое подобие напорных установившихся потоков требует равенства Re, которое у лопастных нагнетателей обычно принимают равным (u2 ·D2) /v. Следствием выполнения этих условий являются:
1) кинематическое подобие во всех точках потоков; при этом любые скорости жидкости
ν~νвх ~n ·L.
2) Равенство числа Эйлера Еu, которое для напорного движения равноg·ΔHст/v2 и, следовательно, пропорционально разности статических напоров ΔHст и скорости жидкости во второй степени.
Режимы работы нагнетателя, при которых выполняются описанные условия, называются подобными. Теория подобия позволяет установить формулы пересчета параметров лопастных нагнетателей, определяющие зависимость подачи, напора, моментов сил и мощности геометрически подобных нагнетателей, работающих на подобных режимах, от их размеров и частоты вращения.
Подача нагнетателя пересчитывается по уравнению (4.1). Напор нагнетателя равен
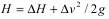
где  - разность соответственно
- разность соответственно
статических и скоростных напоров после нагнетателя и до него.
Напор нагнетателя H представляет собой разность энергии единицы веса потока (жидкости или воздуха) в сечении потока насоса
 и перед ним
и перед ним  и выражается в метрах.
и выражается в метрах.
Эти разности напоров пропорциональны скорости потока во второй степени
ΔHст ~ v2/g; Δv2/(2g)~ v2/g, поэтому напор насоса Н ~v2/g.
Принимая gx = g2, получаем:

Момент сил взаимодействия потока со стенками каналов М~p ·v2 ·L3. Отсюда получим формулу пересчета момента сил

Мощность, передаваемая от вала на рабочее колесо,
Nв = ω ⋅Mв,
где Мв – момент сил, с которым жидкость действует на рабочее колесо (в том числе сил дискового трения).
Учитывая уравнение (4.2), находим
Nв ~ p ·n3 ·L5. (4.3)
Мощность нагнетателя превышает мощность Nв на величину мощности, расходуемой на трение в уплотнении вала и подшипниках. Эта мощность по уравнению (4.3) не пересчитывается. Однако если насос не слишком мал, то потери на трение в уплотнениях вала и в подшипниках малы и для приближенного пересчета мощности насоса можно применять уравнение (4.3). Следовательно,

При соблюдении всех условий подобия расход в щелевых уплотнениях нагнетателя пропорционален его подаче, гидравлические потери в нагнетателе, которые для подобных режимов пропорциональны скорости жидкости во второй степени, пропорциональны напору нагнетателя, дисковые потери мощности пропорциональны мощности Nв. Отсюда следует равенство для подобных режимов объемного и гидравлического КПД и приближенное равенство механического КПД
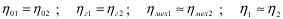
Приведенный выше вывод формул пересчета не связан с особенностями рабочего процесса лопастного нагнетателя, поэтому формулы справедливы не только для лопастных нагнетателей, но и для других видов гидромашин (в том числе двигателей), имеющих вращающиеся рабочие органы или цикличный рабочий процесс.
Мощностью нагнетателя N (потребляемая) называется энергия, подводимая к нему от двигателя за единицу времени. Энергия, при-обретенная за единицу времени жидкостью, прошедшей через нагнетатель, называется полезной мощностью нагнетателя

N >Nn на величину потерь в нагнетателе. Эти потери оцениваются КПД

Геометрическое подобие щелевых уплотнений, шероховатости стенок и толщины лопаток не всегда выполняется. Обычно у более крупных насосов зазоры в уплотнениях, шероховатость и толщина лопаток относительно меньше, чем у малых. Равенство Re для модели и натуры также не всегда удается выполнить. Однако если эти отклонения от подобия невелики, то формулы пересчета дают достаточно точные результаты.
Формулы пересчета для одного и того же нагнетателя, работающего на разных частотах вращения (L1 = L2), принимают вид:

Так как обычно при изменении частоты вращения насоса равенство Re не выдерживается, то формулы (4.4) дают приближенный результат.






