Подобия
Помимо безразмерных величин θ, WXiWy и безразмерных координат, составленных из однородных физических величин, в уравнения входят также безразмерные комплексы, состоящие из разнородных физических величин:

Этим комплексам, называемым числами подобия, присвоены имена ученых, внесших значительный вклад в развитие гидродинамики или теплопередачи.
1. Первый из этих безразмерных комплексов обозначают

и называют числом Нуссельта, или безразмерным коэффициентом теплоотдачи. Число Нуссельта характеризует теплообмен на границе стенка - жидкость. В задачах конвективного теплообмена число Nuобычно искомая величина, поскольку в него входит определяемая величина а.
Несмотря на внешнее сходство с числом Био (Bi)
Bi=(άр δ)/λст,
используемым при изучении теплопроводности, число Нуссельта существенно отличается от него. В число Bi входит коэффициент теплопроводности твердого тела; в число Nu — коэффициент теплопроводности жидкости. Кроме того, в число Био коэффициент теплоотдачи вводится как величина, заданная в условиях однозначности, мы же рассматриваем коэффициент теплоотдачи, входящий в Nu, как величину искомую.
2. Безразмерный комплекс

называют числом Рейнольдса. Оно характеризует соотношение сил инерции и сил вязкости. Число Рейнольдса – важная характеристика как изотермического, так и неизотермического процессов течения жидкости.
3. Третий безразмерный комплекс обозначают

и называют числом Пекле. Его можно преобразовать следующим образом:

Здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель - теплоту, переносимую теплопроводностью.
4. Безразмерный комплекс

называют числом Грасгофа. Оно характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей.
Используя введенные обозначения, систему безразмерных дифференциальных уравнений можно записать в следующем виде:

Безразмерные величины Θ,Wx, Wy, X, У, Nu, Re, Ре, Gr можно рассматривать как новые переменные.
Их можно разделить на три группы:
– независимые переменные - это безразмерные координаты X, У;
– зависимые переменные - это Nu, Θ, Wx, Wy; они однозначно определяются значениями независимых переменных при определенных значениях величин, входящих в условия однозначности;
– постоянные величины - это Ре, Re, Gr; они заданы условиями однозначности и для конкретной задачи являются постоянными. Действительно, числа Ре, Re и Gr состоят только из величин, входящих в условия задачи.
В результате можно написать

Уравнения (3.4) называют уравнениями подобия.
Здесь Хс, Ус соответствуют поверхности теплоотдачи (стенки). Нахождение а (или Nu) для точек пространства, не лежащих на поверхности стенки, не имеет смысла. В рассматриваемой задаче Ус = 0.
Если в уравнении движения учесть член-

то в результате приведения к безразмерной записи появился бы и член
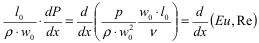
5. Безразмерный комплекс

называют числомЭйлера.Эточисло характеризует соотношение сил давления и сил инерции.
Необходимо отметить, что при неизменной формулировке задачи новые безразмерные величины могут быть получены соответствующим комбинированием старых безразмерных комплексов, однако при этом число переменных под знаком функции не должно измениться.
Например

Числу Прандтля можно придать определенный физический смысл.
Уравнение энергии

и уравнение движения

При a = v расчетные поля температур и скоростей будут подобны, если только аналогичны и условия однозначности. Условию a = v соответствует равенствоРг = 1. Таким образом, при определенных условиях числу Прандтля может быть придан смысл меры подобия полей температур и скоростей.
В зависимости от значения числаРг жидкости делят на три группы: жидкости с числами Рг< 1 (жидкие металлы), теплоносители с Pr = 1(неметаллические капельные жидкости при больших температурах и газы), жидкости с числами Рг> 1 (неметаллические капельные жидкости).
Учитывая, чтоPe=Re·Pr, уравнения подобия можно записать в виде:

Исходя из уравнений (3.5), безразмерные переменные можно разделить на два вида:
– определяемые - что числа, в которые входят искомые зависимые переменные; в рассматриваемом случае зависимыми являются a, θ,:wx и wy, следовательно, определяемыми будут Nu, θ, Wx и Wy;
– определяющие - это числа, целиком составленные из независимых переменных и постоянных величин, входящих в условия однозначности; в рассматриваемом случае определяющими являются X, У, Re, Рг (или Ре) и Gr.






