Министерство образования и науки Российской Федерации
ФГБОУ ВПО «Сибирский государственный технологический университет»
А.С.Михайлов
Методы линейного программирования
Рекомендовано редакционно-издательским советом СибГТУ в качестве курса лекций для студентов направления 230100 Информатика и вычислительная техника, специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем, направления 230400 информационные системы и технологии, специальности 230401 Информационные системы и технологии в промышленности, а также направления 231000 Программная инженерия, специальности Разработка программно-информационных систем очной формы обучения
Красноярск 2011
Михайлов А.С. Методы линейного программирования: курс лекций для студентов направления 230100 Информатика и вычислительная техника, специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем, направления 230400 информационные системы и технологии, специальности 230401 Информационные системы и технологии в промышленности, а также направления 231000 Программная инженерия, специальности Разработка программно-информационных систем очной формы обучения / А.С.Михайлов. – Красноярск: СибГТУ, 2011. – 76с.
Рецензенты:
ст.преподаватель Е.Н.Касьянова (научно-методический совет СибГТУ),
д-р техн. наук, проф. А.В.Медведев (СибГАУ)
Курс лекций предназначен для углубленного изучения теории линейного программирования, содержит доказательства теорем и оснащено многочисленными поясняющими примерами. В нем содержится обширный список литературы для самостоятельного изучения дисциплины. Пособие может быть использовано студентами при выполнении лабораторных работ по дисциплинам «Методы оптимизации» и «Исследование операций», а также преподавателями и аспирантами.
© А.С.Михайлов, 2011
© ФГБОУ ВПО «Сибирский государственный технологический университет», 2011
СОДЕРЖАНИЕ
Введение 4
Тема 1 Введение в ЛП 5
1.1 Исторический экскурс 5
1.2 Ограничения в модели ЛП 5
1.3 Графическое решение задачи ЛП 6
1.4 Графический анализ чувствительности 8
1.4.1 Изменение коэффициентов целевой функции 8
1.4.2 Стоимость ресурсов. 9
Тема 2 Симплекс-метод 13
2.1 Общая постановка задачи ЛП 13
2.2 Некоторые свойства планов 14
2.3 Алгоритм симплекс-метода 16
Тема 3 Двойственная задача и анализ чувствительности 21
3.1 Постановка двойственной задачи 21
3.2 Основные теоремы о двойственности 23
3.3 Решение двойственных задач 24
3.4Двойственный симплекс-метод 25
Тема 4 Анализ чувствительности оптимального решения 28
4.1 Матричное представление симплекс-таблиц 28
4.2 Анализ чувствительности 31
4.2.1 Изменения, влияющие на допустимость решения 32
4.2.2 Изменения, влияющие на оптимальность решения 35
Тема 5 Целочисленное линейное программирование 38
5.1 Метод ветвей и границ 38
5.2 Метод отсекающих плоскостей 43
Тема 6 Транспортная задача 46
6.1 Решение транспортной задачи 46
6.1.1 Постановка транспортной задачи 46
6.1.2 Интерпретация метода потенциалов как симплекс-метода 46
6.1.3 Определение начального решения 48
6.1.4 Метод потенциалов 50
6.2 Задача о назначениях 54
Тема 7. Основы сетевого планирования 56
7.1 Основные понятия теории графов 56
7.2 Метод критического пути 60
Тема 8. Задача о максимальном потоке 65
8.1 Постановка задачи о максимальном потоке 65
8.2 Решение задачи о максимальном потоке. Алгоритм Фалкерсона 67
8.3 Алгоритм Эдмондса -Карпа 71
Приложение А (справочное) Перечень ключевых слов 78
Библиографический список 79
Заключение 80
Введение
Целью данного курса лекций является помощь студентам в приобретении знаний по теоретическим основам методов оптимизации и получении твердых навыков решения практических задач.
Для достижения этой цели в курсе изложены основные понятия, определения, теоремы методов оптимизации, приведены примеры решения типовых задач.
Особое внимание уделено теории двойственности и связанных с ней двойственному симплекс-методу, матричному представлению симплекс-метода, с помощью чего подробно излагается анализ на чувствительность линейных задач.
Кроме того, рассматриваются методы целочисленного программирования: метод ветвей и границ и метод отсечения, а также метод потенциалов для решения транспортных задач и венгерский метод для решения задачи о назначениях.
Две последние темы курса посвящены сетевому программированию. В них вводится определение сетевого графика, излагаются теория критического пути и решение задачи о максимальном потоке
Материал изложен логически последовательно, в доступной для студентов форме, по возможности сопровождается доказательствами теорем и многочисленными примерами решения задач.
Материал, изложенный в курсе лекций, изучается на 3 курсе в V семестре дисциплины «Методы оптимизации» в объеме 18 часов лекционных и 36 часов лабораторных занятий, приведенных в методических указаниях «Решение задач линейного и сетевого программирования» [4] и лабораторном практикуме «Методы оптимизации» [5].
Тема 1 Введение в линейное программирование
План
1 Исторический экскурс
2 Ограничения в модели ЛП
3 Графическое решение задачи ЛП
4 Графический анализ чувствительности.
Исторический экскурс
Своим рождением линейное программирование обязано Леониду Витальевичу Канторовичу, академику, лауреату Государственной (1949), Ленинской (1965) и Нобелевской (1975) премий по экономике. В 1938 году молодому (двадцатипятилетнему) математику, профессору Ленинградского университета Л.В.Канторовичу было предложено помочь фанерному тресту в решении задачи поиска наивыгоднейшего распределения работы восьми лущильных станков по пяти различным номенклатурам материалов при известной производительности каждого станка. Ученый решил эту задачу, а также нашел общее в постановке и решении ряда других (сходных с вышеуказанной) задач:
· как организовать производство, обеспечив максимальное выполнение плана при условии заданного ассортимента?
· как оптимальным образом раскроить материалы?
· как наиболее полно использовать механизмы?
· как оптимально распределить посевную площадь?
· как наилучшим образом выполнить план строительства при данных ресурсах?
· как составить оптимальный план перевозок?
Результаты своих исследований в данном направлении Л.В.Канторович изложил в монографии «Математические методы организации и планирования производства» (1939). Результаты данной работы сыграли огромную роль в оптимальном планировании и были впоследствии отмечены высшими наградами. В США метод линейного программирования был переоткрыт почти 10 лет спустя Дж.Данцигом и Т.Купмансом.
Ограничения в модели линейного программирования
В этом разделе на простом примере с двумя переменными показаны основные элементы модели линейного программирования (ЛП). Далее это пример будет обобщен в общую задачу ЛП.
Пример 1.1
Частная компания производит краску для внутренних и наружных работ из сырья двух типов: М1 и М2. Таблица 1.1 представляет основные данные для задачи.
Отдел маркетинга компании ограничил из-за спроса производство краски для внутренних работ до 2 тонн, а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало более чем на тонну аналогичный показатель производства краски для внешних работ. Компания хочет определить оптимальное (наилучшее) соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.
Таблица 1.1
|
| Расход сырья (в тоннах) на тонну краски | Максимально возможный ежедневный расход сырья | |
| для наружных работ | для внутренних работ | ||
| Сырье М1 | 6 | 4 | 24 |
| Сырье М2 | 1 | 2 | 6 |
| Доход на тонну краски (тыс.руб.) | 5 | 4 | |
Задача (модель) ЛП включает три основных элемента:
1 Переменные, которые следует определить.
2 Целевая функция, подлежащая оптимизации.
3 Ограничения, которым должны удовлетворять переменные.
Переменные модели:
х1 - ежедневный объем производства краски для наружных работ;
х2 - ежедневный объем производства краски для внутренних работ.
Используя эти переменные, далее строим целевую функцию. Логично предположить, что целевая функция (ЦФ), как суммарный ежедневный доход, должна возрастать при увеличении ежедневных объемов красок.
В соответствии с целями компании получаем задачу:
максимизировать z=5x1+4x2. (1.1)
Итак, остался не определенным последний элемент модели - условия (ограничения), которые должны учитывать ограниченные возможности ежедневного потребления сырья и ограниченность спроса на готовую продукцию. Другими словами, ограничения на сырье можно записать следующим образом:
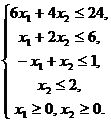 (1.2)
(1.2)






