Уравнения с разделяющимися переменными

К У Р С

В Ы С Ш Е Й

М А Т Е М А Т И К И

 

Краткий курс лекций

 

ЧАСТЬ 3

 

 

2000

 

 

Обыкновенные дифференциальные уравнения.

 

       Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.

       В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.

       Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:

       В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.

 

Тогда получаем: 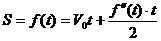 - уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).

 

 

       Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.

 

       Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

 

       Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

 

 

       Пример.

 

 - обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается .

 

 - обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается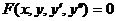

 

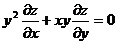 - дифференциальное уравнение в частных производных первого порядка.

       Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

 

Свойства общего решения.

       1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.

 

       2) При каких- либо начальных условиях х = х₀, у(х₀) = у₀ существует такое значение С = С₀, при котором решением дифференциального уравнения является функция у = j(х, С₀).

 

 

       Определение. Решение вида у = j(х, С₀) называется частным решением дифференциального уравнения.

 

       Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С₀), удовлетворяющего начальным условиям у(х₀) = у₀.

 

       Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)

       Если функция f (x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х₀, у₀) в области D, существует единственное решение  уравнения , определенное в некотором интервале, содержащем точку х₀, принимающее при х = х₀ значение j (х₀) = у₀, т.е. существует единственное решение дифференциального уравнения.

 

       Определение. Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.

 

       Пример. Найти общее решение дифференциального уравнения .

 

Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

       Теперь интегрируем: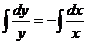          

                                                               - это общее решение исходного дифференциального уравнения.

 

       Допустим, заданы некоторые начальные условия: x₀ = 1; y₀ = 2, тогда имеем

       При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).

 

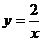
       Определение. Интегральной кривой называется график y = j(x) решения дифференциального уравнения на плоскости ХОY.

 

       Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши.) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.

Особые решения не зависят от постоянной С.

       Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.

       Отметим, что не каждое дифференциальное уравнение имеет особые решения.

 

 

       Пример. Найти общее решение дифференциального уравнения:  Найти особое решение, если оно существует.

       Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0  можно получить из общего решения при С₁ = 0 ошибочно, ведь C ₁ = e^C ¹ 0.

 

 

       Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.

Дифференциальные уравнения первого порядка.

 

       Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:

 

       Если такое соотношение преобразовать к виду  то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.

 

       Преобразуем такое выражение далее:

Функцию f(x,y) представим в виде:  тогда при подстановке в полученное выше уравнение имеем:

 

- это так называемая дифференциальная форма уравнения первого порядка.

 

Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.

 

Уравнения вида y’ = f(x).

 

       Пусть функция f(x) – определена и непрерывна на некотором интервале

a < x < b. В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х₀ и у₀, то можно определить постоянную С.

Уравнения с разделяющимися переменными

 

       Определение. Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде

.

 

 

       Такое уравнение можно представить также в виде:

 

Перейдем к новым обозначениям

 

Получаем:                                     

 

 

       После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.

       Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.

 

 

       Пример. Найти общее решение дифференциального уравнения:

 

           

 

Интеграл, стоящий в левой части, берется по частям (см. Интегрирование по частям.):

 

- это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.

 

Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.

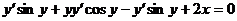
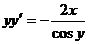 - верно

 

       Пример. Найти решение дифференциального уравнения  при условии у(2) = 1.

 

при у(2) = 1 получаем

Итого: 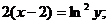   или  - частное решение;

 

       Проверка:  , итого

 

 - верно.

 

       Пример. Решить уравнение

                                                           - общий интеграл

                                                        - общее решение

 

       Пример. Решить уравнение

 

 

 

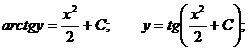
       Пример. Решить уравнение при условии у(1) = 0.

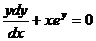
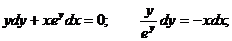
Интеграл, стоящий в левой части будем брать по частям (см.  Интегрирование по частям.).

 

 

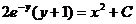
       Если у(1) = 0, то

 

       Итого, частный интеграл: .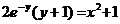

 

 

       Пример. Решить уравнение .

 

 

 

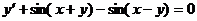
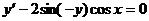
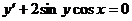
Для нахождения интеграла, стоящего в левой части уравнения см. Таблица основных интегралов. п.16. Получаем общий интеграл:

 

 

       Пример. Решить уравнение

Преобразуем заданное уравнение:

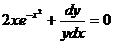
    Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.

 

 

       Пример. Решить уравнение .

 

 

;     ;

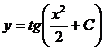
Допустим, заданы некоторые начальные условия х₀ и у₀. Тогда:

 

Получаем частное решение

 

 

Однородные уравнения.

 

       Определение. Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

           

 

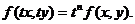
       Пример. Является ли однородной функция

 

 

Таким образом, функция f(x, y) является однородной 3- го порядка.

 

 

       Определение. Дифференциальное уравнение вида называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.

 

       Любое уравнение вида  является однородным, если функции P (x, y) и Q (x, y) – однородные функции одинакового измерения.

 

       Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.

           

       Рассмотрим однородное уравнение

Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:

 

Т.к. параметр t вообще говоря произвольный, предположим, что . Получаем:

       Правая часть полученного равенства зависит фактически только от одного аргумента , т.е.

Исходное дифференциальное уравнение таким образом можно записать в виде:

Далее заменяем y = ux, .

 

таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

 

Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.

 

 

       Пример. Решить уравнение .

 

Введем вспомогательную функцию u.

.

Отметим, что введенная нами функция u всегда положительна, т.к. в противном случае теряет смысл исходное дифференциальное уравнение, содержащее .

Подставляем в исходное уравнение:

 

 

Разделяем переменные:

 

Интегрируя, получаем:

 

Переходя от вспомогательной функции обратно к функции у, получаем общее решение:

 

 

 

Уравнения, приводящиеся к однородным.

 

       Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным.

 

       Это уравнения вида .

Если определитель 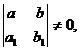 то переменные могут быть разделены подстановкой

где a и b - решения системы уравнений

 

 

       Пример. Решить уравнение

Получаем

 

Находим значение определителя .

Решаем систему уравнений

 

Применяем подстановку  в исходное уравнение:

 

Заменяем переменную  при подстановке в выражение, записанное выше, имеем:

 

Разделяем  переменные:

 

 

Переходим теперь к первоначальной функции у и переменной х.

 

 

Итого, выражение 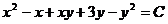 является общим интегралом исходного дифференциального уравнения.

 

 

       В случае если в исходном уравнении вида  определитель  то переменные могут быть разделены подстановкой

 

 

       Пример. Решить уравнение

 

Получаем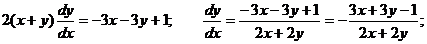

Находим значение определителя

Применяем подстановку

Подставляем это выражение в исходное уравнение:

 

Разделяем переменные:

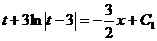
Далее возвращаемся к первоначальной функции у и переменной х.

таким образом, мы получили общий интеграл исходного дифференциального уравнения.

 

 

Линейные уравнения.

 

       Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

при этом, если правая часть Q (x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q (x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением.

 

       P (x) и Q (x)- функции непрерывные на некотором промежутке a < x < b.

 

 

Линейные однородные дифференциальные уравнения.

 

       Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида

.

 

       Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.

 

 Общее решение:                          

           

 

 

Линейные неоднородные дифференциальные уравнения.

 

       Для интегрирования линейных неоднородных уравнений (Q (x) ¹ 0) применяются в основном два метода: метод Бернулли и метод Лагранжа.

 

Метод Бернулли.

(Якоб Бернулли (1654-1705) – швейцарский математик.)

 

       Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций .

       При этом очевидно, что  - дифференцирование по частям.

 

       Подставляя в исходное уравнение, получаем:

       Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.

       Например, функция  может быть представлена как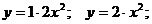

 и т.п.

       Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение .

       Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:

 

 

 

       Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение  с учетом того, что выражение, стоящее в скобках, равно нулю.

 

       Интегрируя, можем найти функцию v:

;      ;

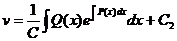       Т.е. была получена вторая составляющая произведения , которое и определяет искомую функцию.

       Подставляя полученные значения, получаем:

 

 

       Окончательно получаем формулу:

, С₂ - произвольный коэффициент.

Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.

 

Метод Лагранжа.

 

(Ларганж Жозеф Луи (1736-1813) - французский математик,  през. Берлинской АН,

поч. чл. Пет. АН (1776)).

 

 

Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной.

 

       Вернемся к поставленной задаче:

 

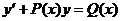
Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.

       Далее находится решение получившегося однородного дифференциального уравнения:

.

Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С₁ некоторой функцией от х.

       Тогда по правилам дифференцирования произведения функций получаем: