Нормальные системы линейных однородных дифференциальных

уравнений с постоянными коэффициентами.

 

       При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.

 

Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде:

                                                                                                     (2)

 

       Решения системы (2) обладают следующими свойствами:

 

1) Если y, z, u – решения системы, то Cy, Cz, Cu, где C = const – тоже являются решениями этой системы.

2) Если y ₁, z ₁, u ₁ и y ₂, z ₂, u ₂ – решения системы, то y ₁ + y ₂, z ₁ + z ₂, u ₁ + u ₂ – тоже являются решениями системы.

 

       Решения системы ищутся в виде:

Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на e^kx, получаем:

Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.:

       В результате вычисления определителя получаем уравнение третьей степени относительно k. Это уравнение называется характеристическим уравнением и имеет три корня k ₁, k ₂, k ₃. Каждому из этих корней соответствует ненулевое решение системы (2):

       Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):

       Пример. Найти общее решение системы уравнений:

Составим характеристическое уравнение:

Решим систему уравнений:

Для k ₁:

Полагая (принимается любое значение), получаем:

 

Для k ₂:

Полагая (принимается любое значение), получаем:

Общее решение системы:

 

           

Этот пример может быть решен другим способом:

 

Продифференцируем первое уравнение:

Подставим в это выражение производную у ¢ = 2 x + 2 y  из второго уравнения.

 

       Подставим сюда у, выраженное из первого уравнения:

 

 

 

       Обозначив , получаем решение системы:

 

Пример. Найти решение системы уравнений

Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т.к. не является однородным (в уравнение входит независимая переменная х).

       Для решения продифференцируем первое уравнение по х. Получаем:

Заменяя значение z ’ из второго уравнения получаем: .

С учетом первого уравнения, получаем:

Решаем полученное дифференциальное уравнение второго порядка.

Общее решение однородного уравнения:

 

Теперь находим частное решение неоднородного дифференциального уравнения по формуле

Общее решение неоднородного уравнения:

 

Подставив полученное значение в первое уравнение системы, получаем:

       Пример. Найти решение системы уравнений:

 

Составим характеристическое уравнение:

 

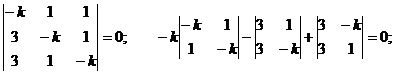
1) k = -1.

Если принять g = 1, то решения в этом случае получаем:

 

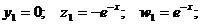
2) k₂ = -2.

Если принять g = 1, то получаем:

 

3) k₃ = 3.

Если принять g = 3, то получаем:

 

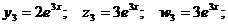
Общее решение имеет вид:

 

 

Элементы теории устойчивости.

 

       Теория устойчивости решений дифференциальных уравнений является одним из разделов качественной теории дифференциальных уравнений, которая посвящена не нахождению какого – либо решения уравнения, а изучению характера поведения этого решения при изменении начальных условий или аргумента.

       Этот метод особенно важен, т.к. позволяет делать вывод о характере решения без непосредственного нахождения этого решения. Т.е. даже в тех случаях, когда решение дифференциального уравнения вообще не может быть найдено аналитически.

       Пусть имеется некоторое явление, описанное системой дифференциальных уравнений:

                                                                     (1)

и начальные условия:

       Для конкретного явления начальные условия определяются опытным путем и поэтому неточны.

 

       Теорема. (о непрерывной зависимости решения от начальных условий)

Если правая часть дифференциального уравнения непрерывна и по переменной у имеет ограниченную частную производную  на области прямоугольника, ограниченного 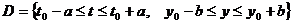, то решение

, удовлетворяющее начальным условиям , непрерывно зависит от начальных данных, т.е. для любого , при котором если

 то  при условии, что

 где

       Эта теорема справедлива как для одного дифференциального уравнения, так и для системы уравнений.

 

       Определение. Если  - решение системы дифференциальных уравнений, то это решение называется устойчивым по Ляпунову, если для любого , такое, что для любого решения  той же системы, начальные условия которого удовлетворяют неравенствам

справедливы неравенства

 

(Ляпунов Александр Михайлович (1857 – 1918) академик Петерб. АН)

 

       Т.е. можно сказать, что решение j(t) устойчиво по Ляпунову, если близкие к нему по начальным условиям решения остаются близкими и при t ³ t ₀.

       Если 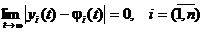, то решение j(t) называется асимптотически устойчивым.

       Исследование на устойчивость по Ляпунову произвольного решения  системы можно свести к исследованию на устойчивость равного нулю решения некоторой другой системы, которая получена из данной заменой неизвестных функций:

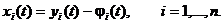
       Тогда:

                            (2)

 

       Система (2) имеет тривиальное (равное нулю) решение

 

       Теорема. Решение  системы (1) устойчиво по Ляпунову тогда и только тогда, когда устойчиво по Ляпунову тривиальное решение системы (2).

       Это тривиальное решение называется положением равновесия или точкой покоя.

 

       Определение. Точка покоя системы (2) устойчива по Ляпунову, если для любого  такое, что из неравенства

следует

.

 

 

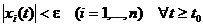       Теорема. (Теорема Ляпунова). Пусть задана система

имеющая тривиальное решение .

       Пусть существует дифференцируемая функция , удовлетворяющая условиям:

       1) ³ 0 и v = 0 только при у₁ = у₂ = … = у _n =0, т.е. функция v имеет минимум в начале координат.

       2) Полная производная функции v вдоль фазовой траектории (т.е. вдоль решения y_i (t) системы (1)) удовлетворяет условию:

при

Тогда точка покоя  устойчива по Ляпунову.

       Если ввести дополнительное требование, чтобы вне сколь угодно малой окрестности начала координат  выполнялось условие

где b - постоянная величина, то точка покоя  асимптотически устойчива.

       Функция v называется функцией Ляпунова.

 

 

Классификация точек покоя.

 

Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами

Характеристическое уравнение этой системы имеет вид:

 

       Рассмотрим следующие возможные случаи:

 

1) Корни характеристического уравнения действительные, отрицательные и различные.

Точка покоя  будет устойчива. Такая точка покоя называется устойчивым узлом.

 

2) Корни характеристического уравнения действительны и

 или .

В этом случае точка покоя также будет устойчива.

 

3) Хотя бы один из корней  положителен.

В этом случае точка покоя неустойчива, и такую точку называют неустойчивым седлом.

 

4) Оба корня характеристического уравнения положительны .

В этом случае точка покоя неустойчива, и такую точку называют неустойчивым узлом.

 

Если полученного решения системы исключить параметр t, то полученная функция  дает траекторию движения в системе координат XOY.

Возможны следующие случаи:

                               b                                         b

 

                                           a                                         a

 

      Устойчивый узел.                Неустойчивый узел.                    Седло.

5) Корни характеристического уравнения комплексные .

Если р = 0, т.е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову.

Такая точка покоя называется центром.

Если p < 0, то точка покоя устойчива и называется устойчивым фокусом.

Если p > 0, то точка покоя неустойчива и называется неустойчивым фокусом.

 

 

Уравнения математической физики.

 

Уравнения в частных производных.

 

       Определение. Дифференциальным уравнением в частных производных называется уравнение относительно неизвестной функции нескольких переменных, ее аргументов и ее частных производных различных порядков.

 

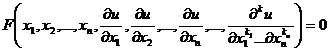
       Порядком дифференциального уравнения в частных производных называется порядок старшей производной, входящей в это уравнение. Решением уравнения будет некоторая функция , которая обращает уравнение в тождество.