физики.
1) Волновое уравнение. (Уравнение колебаний струны, электроколебания, крутильные колебания вала и др.) Это простейшее уравнение гиперболического типа.
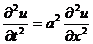
2) Уравнение теплопроводности. (Уравнение Фурье) Это простейшее уравнение параболического типа. Описывает процессы теплопроводности, фильтрации жидкости и газа, некоторые вопросы теории вероятностей.
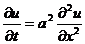
3) Уравнение Лапласа. Это простейшее уравнение эллиптического типа. Описывает магнитные и электрические поля, гидродинамику, диффузию и др.
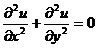
В этих уравнениях функция u зависит от двух переменных, однако, задача может быть расширена для случая трех переменных:
1) Волновое уравнение: 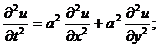
2) Уравнение теплопроводности: 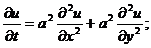
3) Уравнение Лапласа: 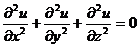
Рассмотрим подробнее каждое из этих уравнений.
Уравнение колебаний струны.
Определение. В математической физике струной называется тонкая нить, в которой возможно возникновение напряжений только в продольном, но не в поперечном направлении.
Пусть концы натянутой струны закреплены в точках х = а и x = b, возникающие в ней напряжения обозначим Т. Будем также считать, что плотность струны постоянна на всем ее протяжении.
Допустим, что в момент t0 = 0 струна выведена из состояния равновесия и совершает малые колебания.
Отклонение струны в каждой точке с координатой х в момент времени t обозначим как
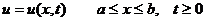
 u
u
C
B a
A
D
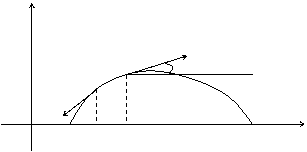
0 a x x+Dx b x
На произвольный элемент длины нити (х, х + Dх) действуют две силы натяжения
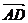 и
и  . При этом:
. При этом:
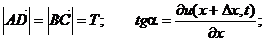
Если считать колебания малыми, то можно принять:
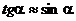
Тогда проекция силы  на ось u:
на ось u:
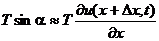
Проекция силы 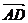 на ось u:
на ось u:

Находим сумму этих проекций:
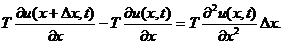
Выражение, стоящее в правой части равенства получено в результате применения теоремы Лагранжа (см. Теорема Лагранжа) к выражению, стоящему слева.
Произведение массы на ускорение рассматриваемого элемента струны равно:
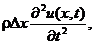
где r - плотность струны.
Приравнивая полученное выражение к значению проекции силы, получим:
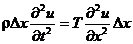

Или 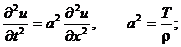
Для полного определения движения струны полученного уравнения недостаточно. Функция u (x, t) должна еще удовлетворять граничным условиям, описывающим состояние струны на концах (в точках x = a и x = b) и начальным условиям, описывающим состояние струны в момент времени t = 0.
Совокупность граничных и начальных условий называется краевыми условиями.
Таким образом, задача Коши состоит в нахождении решения линейного дифференциального уравнения с частными производными второго порядка при начальных условиях

и краевых условиях
 .
.
Начальные условия показывают, в каком положении находится струна в начальный момент времени и скорость каждой ее точки в начальный момент времени.
Функции f (x) и F (x) заданы.
Краевые условия показывают, что концы струны закреплены в точках a = 0, b = l
Решение задачи Коши методом разделения переменных.
(Метод Фурье.)
Решение уравнения
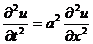
будем искать в виде  при граничных условиях:
при граничных условиях:
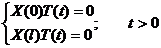
Тогда X (0) = X (l) = 0.
Подставим решение в исходное уравнение:

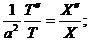
Можно показать, что функции Х и Т имеют вид:
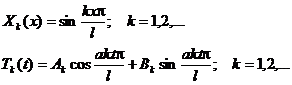
Все решения исходного дифференциального уравнения, удовлетворяющие граничным условиям, можно записать в виде:
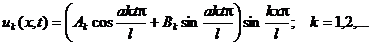
Окончательно решение уравнения колебаний струны можно записать в виде:

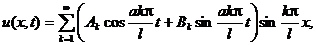
где 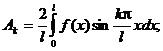
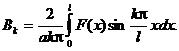
Решение задачи Коши методом Даламбера.
(Жан Лерон Д’Ламбер (1717 – 1783) – французский математик)
В случае если длина струны очень велика, то на колебания, возникающие в середине струны, концы струны влияния практически не оказывают. Поэтому, рассматривая колебания бесконечной струны, уравнение
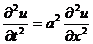
решается только при начальных условиях:
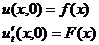
Для нахождения решения введем новые переменные:

Тогда исходное уравнение принимает вид:
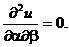
Решением этого уравнения будет функция 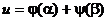 , где j и y - некоторые функции, которые будем считать дважды дифференцируемыми.
, где j и y - некоторые функции, которые будем считать дважды дифференцируемыми.

Получаем: 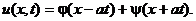
Если продифференцировать полученный ответ, получим:
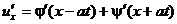
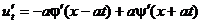
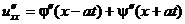
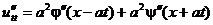
Т.е. 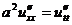 .
.
Далее с использованием начальных условий находим функции j и y.
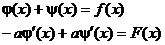
Проинтегрировав последнее равенство на отрезке [0, x], получаем:
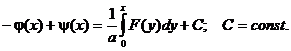
Тогда:
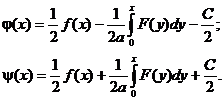
Решение задачи Коши получаем в виде:


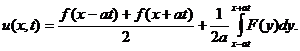
Эта формула называется формулой Даламбера.
Уравнение теплопроводности.
Температуру физического тела в произвольной точке с координатами (x, y, z) в момент времени t можно представить в виде функции:
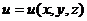
Составим дифференциальное уравнение:
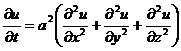
Выражение 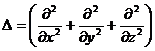 называется оператором Лапласа.
называется оператором Лапласа.
Тогда составленное нами дифференциальное уравнение принимает вид:
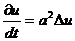
и называется уравнением теплопроводности в пространстве.
В качестве частных случаев рассматривают:
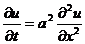 - уравнение теплопроводности в стержне,
- уравнение теплопроводности в стержне,
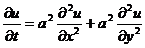 - уравнение теплопроводности на плоскости.
- уравнение теплопроводности на плоскости.
В случае рассмотрения уравнения теплопроводности в стержне искомая функция u (x, t) должна удовлетворять записанному выше дифференциальному уравнению, начальному условию 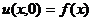
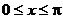 и граничным условиям
и граничным условиям 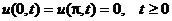 .
.
В результате решения дифференциального уравнения методом Фурье получим:
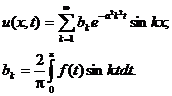
Отметим, что распространение тепла в теле называется стационарным, если функция u не зависит от времени t.
Уравнение Лапласа.
Определение. Функция 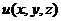 называется гармонической на области s, если она имеет непрерывные частные производные второго порядка на области s и удовлетворяет условию
называется гармонической на области s, если она имеет непрерывные частные производные второго порядка на области s и удовлетворяет условию
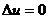 ,
,
где D - оператор Лапласа.
Уравнение  называется уравнением Лапласа.
называется уравнением Лапласа.
Если на некоторой границе Г тела поддерживать постоянную температуру  , где f – заданная функция, то внутри тела установится единственная постоянная температура. С физической точки зрения это утверждение очевидно, однако, данный факт может быть доказан математически.
, где f – заданная функция, то внутри тела установится единственная постоянная температура. С физической точки зрения это утверждение очевидно, однако, данный факт может быть доказан математически.
Математическое доказательство этого факта называется задачей Дирихле.
(Петер Густав Дирихле (1805 – 1859) – немецкий математик)
Решение задачи Дирихле для круга.
Пусть в плоскости XOY имеется круг радиуса R с центром в начале координат и на его окружности задана функция f (j), где j - полярный угол.
Требуется найти функцию 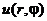 , которая удовлетворяет уравнению Лапласа
, которая удовлетворяет уравнению Лапласа
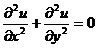
и при 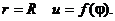
Запишем уравнение Лапласа в полярных координатах:

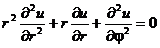
Полагаем  Подставляя это соотношение в уравнение Лапласа, получаем:
Подставляя это соотношение в уравнение Лапласа, получаем:
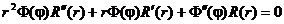
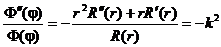
Таким образом, имеем два уравнения:
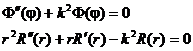
Общее решение первого уравнения имеет вид: 
Решение второго уравнения ищем в виде: 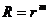 . При подстановке получим:
. При подстановке получим:

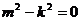
Общее решение второго уравнения имеет вид: 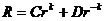 .
.
Подставляя полученные решения в уравнение 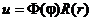 , получим:
, получим:

Эта функция будет решением уравнения Лапласа при любом k ¹ 0.
Если k = 0, то 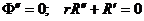 следовательно
следовательно 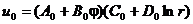 .
.
Решение должно быть периодическим, т.к. одно и то же значение будет повторяться через 2p. (Тогда рассматривается одна и та же точка круга.) Поэтому В0 = 0.
Решение должно быть конечным и непрерывным, поэтому D0 = 0.

Окончательно получаем: 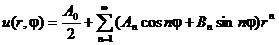
При этом: 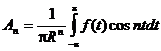
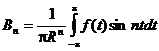
Если подставить эти коэффициенты в полученную выше формулу и произвести упрощение, получаем окончательный результат решения задачи Дирихле, который называется интегралом Пуассона.
(Симеон Дени Пуассон (1781 – 1840) – французский математик)


Ряды.
Основные определения.
Определение. Сумма членов бесконечной числовой последовательности 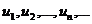 называется числовым рядом.
называется числовым рядом.
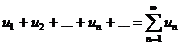
При этом числа 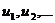 будем называть членами ряда, а un – общим членом ряда.
будем называть членами ряда, а un – общим членом ряда.
Определение. Суммы 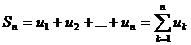 , n = 1, 2, … называются частными (частичными) суммами ряда.
, n = 1, 2, … называются частными (частичными) суммами ряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S 1, S 2, …, Sn, …
Определение. Ряд 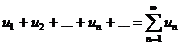 называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.
называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.

Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Свойства рядов.
1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.
2) Рассмотрим два ряда  и
и  , где С – постоянное число.
, где С – постоянное число.
Теорема. Если ряд  сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд  тоже сходится, и его сумма равна С S. (C ¹ 0)
тоже сходится, и его сумма равна С S. (C ¹ 0)
3) Рассмотрим два ряда  и
и 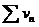 . Суммой или разностью этих рядов будет называться ряд
. Суммой или разностью этих рядов будет называться ряд 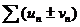 , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды  и
и 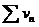 сходятся и их суммы равны соответственно S и s, то ряд
сходятся и их суммы равны соответственно S и s, то ряд 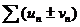 тоже сходится и его сумма равна S + s.
тоже сходится и его сумма равна S + s.
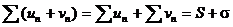
Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Критерий Коши.
(необходимые и достаточные условия сходимости ряда)
Для того, чтобы последовательность 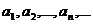 была сходящейся, необходимо и достаточно, чтобы для любого
была сходящейся, необходимо и достаточно, чтобы для любого 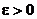 существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:
существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:
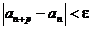 .
.
Доказательство. (необходимость)
Пусть 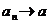 , тогда для любого числа
, тогда для любого числа 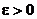 найдется номер N такой, что неравенство
найдется номер N такой, что неравенство
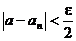 выполняется при n>N. При n>N и любом целом p>0 выполняется также неравенство
выполняется при n>N. При n>N и любом целом p>0 выполняется также неравенство 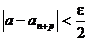 . Учитывая оба неравенства, получаем:
. Учитывая оба неравенства, получаем:
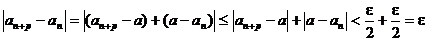
Необходимость доказана. Доказательство достаточности рассматривать не будем.
Сформулируем критерий Коши для ряда.
Для того, чтобы ряд 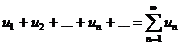 был сходящимся необходимо и достаточно, чтобы для любого
был сходящимся необходимо и достаточно, чтобы для любого 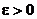 существовал номер N такой, что при n > N и любом p >0 выполнялось бы неравенство
существовал номер N такой, что при n > N и любом p >0 выполнялось бы неравенство
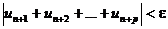 .
.
Однако, на практике использовать непосредственно критерий Коши не очень удобно. Поэтому как правило используются более простые признаки сходимости:
1) Если ряд  сходится, то необходимо, чтобы общий член un стремился к нулю. Однако, это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, так называемый гармонический ряд
сходится, то необходимо, чтобы общий член un стремился к нулю. Однако, это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, так называемый гармонический ряд 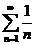 является расходящимся, хотя его общий член и стремится к нулю.
является расходящимся, хотя его общий член и стремится к нулю.
Пример. Исследовать сходимость ряда 
Найдем 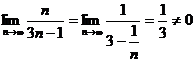 - необходимый признак сходимости не выполняется, значит ряд расходится.
- необходимый признак сходимости не выполняется, значит ряд расходится.
2) Если ряд сходится, то последовательность его частных сумм ограничена.
Однако, этот признак также не является достаточным.
Например, ряд 1-1+1-1+1-1+ … +(-1)n+1+… расходится, т.к. расходится последовательность его частных сумм в силу того, что
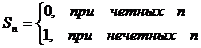
Однако, при этом последовательность частных сумм ограничена, т.к. 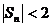 при любом n.
при любом n.
Ряды с неотрицательными членами.
При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами.
Теорема. Для сходимости ряда  с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.
с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.
Признак сравнения рядов с неотрицательными членами.
Пусть даны два ряда  и
и 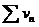 при u n, vn ³ 0.
при u n, vn ³ 0.
Теорема. Если un £ vn при любом n, то из сходимости ряда 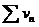 следует сходимость ряда
следует сходимость ряда  , а из расходимости ряда
, а из расходимости ряда  следует расходимость ряда
следует расходимость ряда 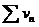 .
.
Доказательство. Обозначим через Sn и s n частные суммы рядов  и
и 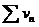 . Т.к. по условию теоремы ряд
. Т.к. по условию теоремы ряд 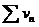 сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ s n то частные суммы ряда
сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ s n то частные суммы ряда  тоже ограничены, а этого достаточно для сходимости.
тоже ограничены, а этого достаточно для сходимости.
Пример. Исследовать на сходимость ряд 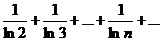
Т.к. 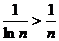 , а гармонический ряд
, а гармонический ряд 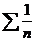 расходится, то расходится и ряд
расходится, то расходится и ряд  .
.
Пример. Исследовать на сходимость ряд 
Т.к. 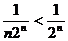 , а ряд
, а ряд 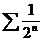 сходится (как убывающая геометрическая прогрессия), то ряд
сходится (как убывающая геометрическая прогрессия), то ряд 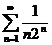 тоже сходится.
тоже сходится.
Также используется следующий признак сходимости:
Теорема. Если  и существует предел
и существует предел 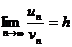 , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды  и
и 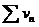 ведут одинаково в смысле сходимости.
ведут одинаково в смысле сходимости.
Признак Даламбера.
(Жан Лерон Даламбер (1717 – 1783) – французский математик)
Если для ряда  с положительными членами существует такое число q <1, что для всех достаточно больших n выполняется неравенство
с положительными членами существует такое число q <1, что для всех достаточно больших n выполняется неравенство
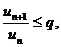
то ряд  сходится, если же для всех достаточно больших n выполняется условие
сходится, если же для всех достаточно больших n выполняется условие

то ряд  расходится.
расходится.
Предельный признак Даламбера.
Предельный признак Даламбера является следствием из приведенного выше признака Даламбера.
Если существует предел 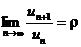 , то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя.
, то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя.
Пример. Определить сходимость ряда 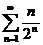 .
.
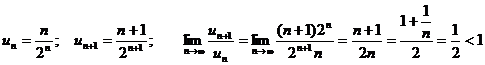
Вывод: ряд сходится.
Пример. Определить сходимость ряда 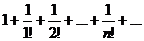
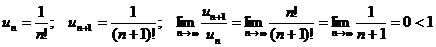
Вывод: ряд сходится.
Признак Коши. (радикальный признак)
Если для ряда  с неотрицательными членами существует такое число q <1, что для всех достаточно больших n выполняется неравенство
с неотрицательными членами существует такое число q <1, что для всех достаточно больших n выполняется неравенство
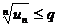 ,
,
то ряд  сходится, если же для всех достаточно больших n выполняется неравенство
сходится, если же для всех достаточно больших n выполняется неравенство
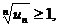
то ряд  расходится.
расходится.
Следствие. Если существует предел 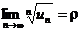 , то при r<1 ряд сходится, а при r>1 ряд расходится.
, то при r<1 ряд сходится, а при r>1 ряд расходится.
Пример. Определить сходимость ряда 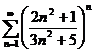 .
.

Вывод: ряд сходится.
Пример. Определить сходимость ряда 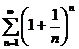 .
.
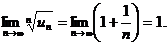
Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.
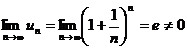 ,
,
таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.
Интегральный признак Коши.
Если j (х) – непрерывная положительная функция, убывающая на промежутке [1;¥), то ряд j (1) + j (2) + …+ j (n) + … =  и несобственный интеграл
и несобственный интеграл 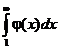 одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Пример. Ряд 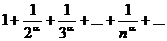 сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл
сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл 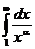 сходится при a>1 и расходится a£1. Ряд
сходится при a>1 и расходится a£1. Ряд 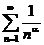 называется общегармоническим рядом.
называется общегармоническим рядом.
Следствие. Если f (x) и j (х) – непрерывные функции на интервале (a, b] и 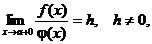 то интегралы
то интегралы 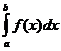 и
и 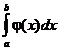 ведут себя одинаково в смысле сходимости.
ведут себя одинаково в смысле сходимости.
Знакопеременные ряды.
Знакочередующиеся ряды.
Знакочередующийся ряд можно записать в виде:
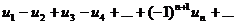
где 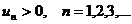
Признак Лейбница.
Если у знакочередующегося ряда 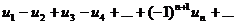 абсолютные величины ui убывают
абсолютные величины ui убывают 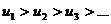 и общий член стремится к нулю
и общий член стремится к нулю  , то ряд сходится.
, то ряд сходится.
Абсолютная и условная сходимость рядов.
Рассмотрим некоторый знакопеременный ряд (с членами произвольных знаков).
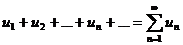 (1)
(1)
и ряд, составленный из абсолютных величин членов ряда (1):
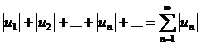 (2)
(2)
Теорема. Из сходимости ряда (2) следует сходимость ряда (1).
Доказательство. Ряд (2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого e>0 существует число N, такое, что при n>N и любом целом p>0 верно неравенство:
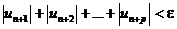
По свойству абсолютных величин:
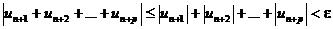
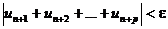
То есть по критерию Коши из сходимости ряда (2) следует сходимость ряда (1).
Определение. Ряд  называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 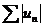 .
.
Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.
Определение. Ряд  называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд 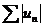 расходится.
расходится.
Признаки Даламбера и Коши для знакопеременных рядов.
Пусть  - знакопеременный ряд.
- знакопеременный ряд.
Признак Даламбера. Если существует предел 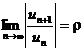 , то при r<1 ряд
, то при r<1 ряд  будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
Признак Коши. Если существует предел  , то при r<1 ряд
, то при r<1 ряд  будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
Свойства абсолютно сходящихся рядов.
1) Теорема. Для абсолютной сходимости ряда  необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.
необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.
Следствие. Условно сходящийся ряд является разностью двух расходящихся рядов с неотрицательными стремящимися к нулю членами.
2) В сходящемся ряде любая группировка членов ряда, не изменяющая их порядка, сохраняет сходимость и величину ряда.
3) Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также абсолютно сходится и имеет ту же сумму.
Перестановкой членов условно сходящегося ряда можно получить условно сходящийся ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
4) Теорема. При любой группировке членов абсолютно сходящегося ряда (при этом число групп может быть как конечным, так и бесконечным и число членов в группе может быть как конечным, так и бесконечным) получается сходящийся ряд, сумма которого равна сумме исходного ряда.
5) Если ряды 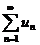 и
и 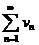 сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида
сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида 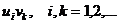 взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S × s - произведению сумм перемножаемых рядов.
взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S × s - произведению сумм перемножаемых рядов.
Если же производить перемножение условно сходящихся рядов, то в результате можно получить расходящийся ряд.
Функциональные последовательности.
Определение. Если членами ряда будут не числа, а функции от х, то ряд называется функциональным.
Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится.
Совокупность таких значений называется областью сходимости.
Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:

Определение. Последовательность { fn (x) } сходится к функции f (x) на отрезке [a,b], если для любого числа e>0 и любой точки х из рассматриваемого отрезка существует номер N = N(e, x), такой, что неравенство
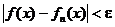
выполняется при n>N.
При выбранном значении e>0 каждой точке отрезка [a,b] соответствует свой номер и, следовательно, номеров, соответствующих всем точкам отрезка [a,b], будет бесчисленное множество. Если выбрать из всех этих номеров наибольший, то этот номер будет годиться для всех точек отрезка [a,b], т.е. будет общим для всех точек.
Определение. Последовательность { fn (x) } равномерно сходится к функции f (x) на отрезке [a,b], если для любого числа e>0 существует номер N = N(e), такой, что неравенство
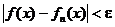
выполняется при n>N для всех точек отрезка [a,b].
Пример. Рассмотрим последовательность 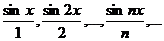
Данная последовательность сходится на всей числовой оси к функции f (x)=0, т.к.

Построим графики этой последовательности:
 sinx
sinx 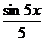

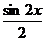
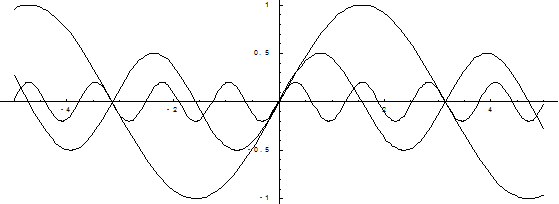
Как видно, при увеличении числа n график последовательности приближается к оси х.
Функциональные ряды.
Определение. Частными (частичными) суммами функционального ряда 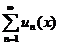 называются функции
называются функции 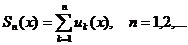
Определение. Функциональный ряд 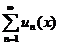 называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательности
называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательности 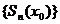 называется суммой ряда
называется суммой ряда 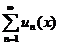 в точке х0.
в точке х0.
Определение. Совокупность всех значений х, для которых сходится ряд 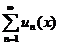 называется областью сходимости ряда.
называется областью сходимости ряда.
Определение. Ряд 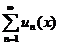 называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
Теорема. (Критерий Коши равномерной сходимости ряда)
Для равномерной сходимости ряда 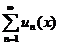 необходимо и достаточно, чтобы для любого числа e >0 существовал такой номер N (e), что при n > N и любом целом p >0 неравенство
необходимо и достаточно, чтобы для любого числа e >0 существовал такой номер N (e), что при n > N и любом целом p >0 неравенство
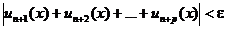
выполнялось бы для всех х на отрезке [ a, b ].
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд 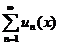 сходится равномерно и притом абсолютно на отрезке [ a, b ], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами:
сходится равномерно и притом абсолютно на отрезке [ a, b ], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами:

т.е. имеет место неравенство:
 .
.
Еще говорят, что в этом случае функциональный ряд 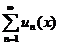 мажорируется числовым рядом
мажорируется числовым рядом 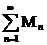 .
.
Пример. Исследовать на сходимость ряд 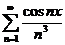 .
.
Так как 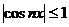 всегда, то очевидно, что
всегда, то очевидно, что 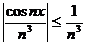 .
.
При этом известно, что общегармонический ряд 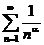 при a=3>1 сходится, то в соответствии с признаком Вейерштрасса исследуемый ряд равномерно сходится и притом в любом интервале.
при a=3>1 сходится, то в соответствии с признаком Вейерштрасса исследуемый ряд равномерно сходится и притом в любом интервале.
Пример. Исследовать на сходимость ряд 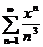 .
.
На отрезке [-1,1] выполняется неравенство  т.е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах (-µ, -1) È (1, µ) расходится.
т.е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах (-µ, -1) È (1, µ) расходится.
Свойства равномерно сходящихся рядов.
1) Теорема о непрерывности суммы ряда.
Если члены ряда 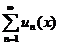 - непрерывные на отрезке [ a, b ] функции и ряд сходится равномерно, то и его сумма S (x) есть непрерывная функция на отрезке [ a, b ].
- непрерывные на отрезке [ a, b ] функции и ряд сходится равномерно, то и его сумма S (x) есть непрерывная функция на отрезке [ a, b ].
2) Теорема о почленном интегрировании ряда.
Равномерно сходящийся на отрезке [ a, b ] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [ a, b ], сходится к интегралу от суммы ряда по этому отрезку.

3) Теорема о почленном дифференцировании ряда.
Если члены ряда 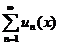 сходящегося на отрезке [ a, b ] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных
сходящегося на отрезке [ a, b ] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных  сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
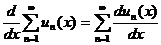
На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.
На практике часто применяется разложение функций в степенной ряд.
Степенные ряды.
Определение. Степенным рядом называется ряд вида
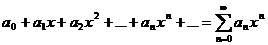 .
.
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Пример. Исследовать на сходимость ряд 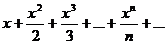
Применяем признак Даламбера:
 .
.
Получаем, что этот ряд сходится при 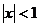 и расходится при
и расходится при  .
.
Теперь определим сходимость в граничных точках 1 и –1.
При х = -1: 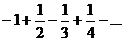 ряд сходится по признаку Лейбница (см. Признак Лейбница.).
ряд сходится по признаку Лейбница (см. Признак Лейбница.).
При х = 1: 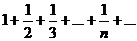 ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд).
Теоремы Абеля.
(Нильс Хенрик Абель (1802 – 1829) – норвежский математик)
Теорема. Если степенной ряд 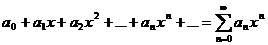 сходится при x = x 1, то он сходится и притом абсолютно для всех
сходится при x = x 1, то он сходится и притом абсолютно для всех 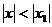 .
.
Доказательство. По условию теоремы, так как члены ряда ограничены, то
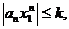
где k - некоторое постоянное число. Справедливо следующее неравенство:
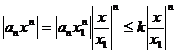
Из этого неравенства видно, что при x < x 1 численные величины членов нашего ряда будут меньше (во всяком случае не больше) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую прогрессию. Знаменатель этой прогрессии  по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд.
по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд.
Поэтому на основании признака сравнения делаем вывод, что ряд 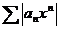 сходится, а значит ряд
сходится, а значит ряд 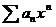 сходится абсолютно.
сходится абсолютно.
Таким образом, если степенной ряд 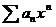 сходится в точке х1, то он абсолютно сходится в любой точке интервала длины 2
сходится в точке х1, то он абсолютно сходится в любой точке интервала длины 2 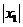 с центром в точке х = 0.
с центром в точке х = 0.
Следствие. Если при х = х1 ряд расходится, то он расходится для всех 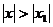 .
.
Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что 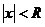 ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех 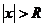 ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.
ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.
Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.
Радиус сходимости может быть найден по формуле:
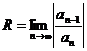
Пример. Найти область сходимости ряда 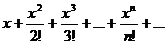
Находим радиус сходимости 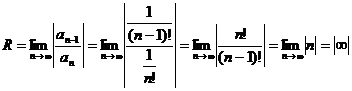 .
.
Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю.
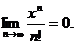
Теорема. Если степенной ряд 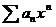 сходится для положительного значения х=х1, то он сходится равномерно в любом промежутке внутри
сходится для положительного значения х=х1, то он сходится равномерно в любом промежутке внутри 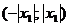 .
.
Действия со степенными рядами.






