Измерительной системы
Эти погрешности связаны с тем, что фактические условия измерений не полностью отражены в моделях, которые описываются статическими уравнениями преобразования элементов измерительной системы.
Относительную погрешность определяют го формуле 
, в которой 
и 
– соответственно измеренное и действительное значение определяемой величины.
При тензорезисторных измерениях можно выделить четыре основных группы систематических погрешностей: геометрическая погрешность, обусловленная базой тензорезистора; погрешность от влияния температуры; погрешность преобразования мостовой схемы и динамическая погрешность электрической цепи измерительной системы.
Геометрическая погрешность тензорезистора обусловлена его геометрической характеристикой преобразования, которая устанавливает зависимость деформации тензорезистора от деформации детали.
В соответствии со схемой рис. 5.13 эту зависимость можно описать уравнением
, (5.25)
где 
– закон изменения деформации детали в направлении, совпадающем с продольной (главной) осью тензорезистора; 
– координата центра тензорезистора; 
– база тензорезистора; 
– деформация тензорезистора; 
– изменение базы, вызванное деформацией детали.
На основании уравнения (5.6) сигнал тензорезистора пропорционален его деформации 
,которую отождествляют и деформацией детали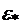 
в точке, совпадающей с центром тензорезистора.
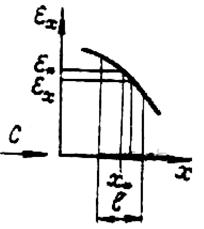
Рис. 5.13. Схема формирования геометрической погрешности
преобразования деформации детали в деформацию тензорезистора
При этом возникает систематическая геометрическая погрешность, которую необходимо учитывать при выборе базы тензорезистора.
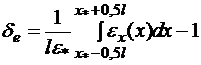. (5.26)
Для определения погрешности необходимо установить вид функции . Это можно сделать из теоретических соображений или на основании исследований аналогичных конструкций.
Если в пределах базы тензорезистора деформация детали изменяется по линейному закону, то геометрической погрешности нет.
При статических и относительно медленных динамических нагрузках влияние базы тензорезистора на результат измерений нужно учитывать только в зонах концентрации деформаций.
При высокочастотных и ударных нагрузках существенная нелинейность распределения деформаций возникает вне зон их концентрация и связана с волновыми процессами формирования деформированного состояния детали. В этом случае для оценки геометрической погрешности закон изменения деформаций по координате и времени можно принять синусоидальным:
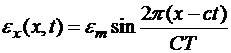, (5.27)
где – текущее время; 
– время колебаний; 
– скорость распространения волны деформаций.
Уравнение (5.26) преобразуется к виду
. (5.28)
Формула (5.28) позволяет оценить динамические свойства тензорезистора, обусловленные его базой.
Скорость распространения волны упругих деформаций зависит от типа детали (стержень, балка, пластина), вида нагрузки (продольная сила, изгибающий или крутящий момент), физико-механических характеристик материала (плотность, упругие постоянные) и от относительной толщины детали.
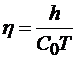, (5.29)
где 
- диаметр стержня или толщина балки, пластины; С0 – «стержневая скорость», определяемая по формуле:
, (5.30)
где 
- плотность материала.
Рис. 5.14. Зависимость скорости продольной волны (1) и волны
изгиба (2) в балках и пластинах от относительной толщины
На рис. 5.14 приведены типичные зависимости скоростей волн от относительной толщины для стержней и балок при действии продольной силы и изгибающего момента. Для определения геометрической погрешности эти зависимости можно применить к деталям другой формы (стержни некруглого поперечного сечения, трубы, пластины) из материалов с коэффициентом Пуассона 0,25…0,35.
Волна кручения (сдвига), вызванная действием крутящего момента, распространяется в деталях любой формы и размеров со скоростью
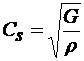. (5.31)
В качестве примера оценим влияние базы тензорезистора на погрешность измерений деформаций на поверхности стальной пластины (
, МПа 
кг/м3) толщиной 
мм, нагруженной изгибающим моментом с частотой колебаний 
кГц.
По формуле (5.30) 
м/с. Для периода колебаний 
с по формуле (6.29) определяем относительную толщину 
, а по графику 2 на рис. 6.14 находим скорость волны изгиба, которая при 
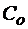равна 1400 м/с. Результаты определения погрешности по формуле (5.28) в зависимости от базы тензорезистора приведены в таблице 5.1.
Таблица 5.1
| , мм
| 1 | 3 | 5 | 10 |
 , %
| 0,2 | 1,8 | 4,8 | 18 |
Для измерений с погрешностью менее 2% в этих условиях необходимо применять тензорезисторы с базой не более 3 мм.
Результаты специальных экспериментов показали, что чувствительность тензорезистора практически не зависит от скорости деформирования. Как элемент электрической цели тензорезистор обладает чисто активным сопротивлением при частотах от 0,5 МГц, если сопротивление изоляции между тензорезистором и деталью не менее 500 МОм. Эта величина практически реализуется для большинства тензорезисторов.
Следовательно, частотный диапазон применения тензорезистора ограничен только геометрической погрешностью , рассчитанной по формуле (5.28).
Погрешность от влияния температуры в основном связана с температурными деформациями детали в зоне наклейки тензорезистора. Эту погрешность можно исключить двумя способами. Первый основан на применении специальных термокомпенсированных тензорезисторов. Второй – на свойства мостовой схемы вычитать сигналы смежных ветвей. В ветвь моста, смежную с активной (рис. 5.11), включают тензорезистор, аналогичный рабочему, который наклеен на модель детали, расположенную в одинаковых с исследуемой деталью физических условиях, но не воспринимающую нагрузок. Точность температурной компенсации проверяют при изменении температуры модели и детали, без нагружения последней.
Погрешность преобразования мостовой схемы связана с применением линеаризированного уравнения (5.20), при выводе которого пренебрегали величинами 
в знаменателе и их квадратами в числителе.
Если тензорезисторы включены в одну или две противоположные ветви мостовой схемы, то погрешность мостовой схемы можно оценить по формуле
. (5.32)
Если тензорезисторы включены в смежные ветви, то – по формуле
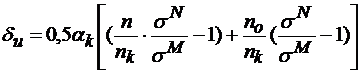, (5.33)
Динамическую погрешность электрической цепи измерительной системы можно оценить на основании переходной характеристики, представляющей собой выходной сигнал системы 
при входном сигнале в виде единичной функции времени
при 
,
при 
.
Тензорезисторные измерительные системы обычно предназначены для регистрации сигналов с постоянной составляющей, а их динамические характеристики по высоким частотам ограничены в основном емкостными связями. Для таких систем переходную характеристику можно аппроксимировать формулой 
, а динамическую характеристику представить уравнением
, (5.34)
где 
– переменная интегрирования, соответствующая произвольному моменту времени в интервале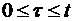 
; 
– основание натурального логарифма; 
- постоянная времени, ее можно рассчитать по формуле 
, где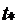 
– время нарастания фронта переходной характеристики от уровня 0,1 до уровня 0,9 от установившегося значения выходного сигнала в соответствии со схемой рис. 5.15.
Для синусоидального входного сигнала, описываемого уравнением (5.27), на основании (5.24) динамическую погрешность можно определить по формуле
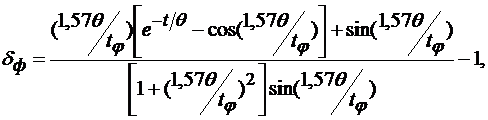(5.35)
где 
– длительность фронта сигнала переходного процесса динамического деформирования при ударных нагрузках или четверть периода установившихся колебаний.
Рис. 5.15.Переходная характеристика
Если ограничить динамическую погрешность величиной 
, то при измерении амплитуды деформации 
необходимо, чтобы постоянная времени системы была 
, а для измерения деформации на фронте импульса на уровне 
необходимо иметь 
.
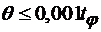При применении тензорезисторов с базой менее 5 мм часто не учитывают их поперечную чувствительность и вместо формулы (5.7) применяют упрощенную, формулу
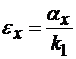, (5.36)
При этом возникает систематическая погрешность определения деформацией
, (5.37)
Например, для фольговых тензорезисторов некоторых конструкций при базе 
мм поперечная чувствительность 
. Если не учесть эту величину, то при измерениях в условиях, когда 
, возникают погрешности 
, 
, 
.
Изготовители тензорезисторов не приводят значений поперечной чувствительности. Для фольговых тензорезисторов Киевского объединения «Вега» типа КФ4 и КФ5 с базами 
мм можно считать 
. При применении других типов тензорезисторов с базами 
мм необходимо определять их поперечную чувствительность по формуле
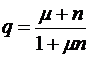, (5.38)
где 
– коэффициент Пуассона калибровочной балки;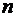 
– величина, рассчитываемая по формуле
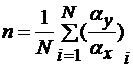, (5.39)
где 
и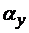 
– сигналы тензорезисторов, наклеенных вдоль и поперек калибровочной балки в «одной» точке; 
= 5…10 – число пар тензорезисторов данной партии.
