В настоящее время существует большое количество разновидностей метода муаровых полос. Мы рассмотрим только один метод, когда сетка параллельных линий наносится непосредственно на поверхность исследуемой детали и деформируется вместе с этой поверхностью. При наложении изображений сеток до и после деформации возникает картина муаровых полос. При этом наложении осуществляется фотографирование деформированной сетки через недеформированную «эталонную сетку», нанесенную на прозрачную пластинку и наложенную на поверхность детали. В полиграфии систему линий с одинаковым шагом называют растром. В случае однородной равномерной деформации (сдвига или растяжения), образующиеся муаровые полоса представляют собой систему чередующихся параллельных (расположенных на одинаковом расстоянии друг от друга) линий. Определение деформаций тела по такой картине полос не представляет труда и, вообще говоря, такие случаи не представляют интереса.
В случае неоднородной деформации более удобной для анализа является интерпретация полос как линий уровня поля перемещений. Если сетка линий нанесена параллельно оси У, то муаровые полосы являются геометрическим местом точек, имеющих одинаковую компоненту перемещения U. При этом разница в значениях U для соседних полос равна шагу эталонного растра. Если изобразить поверхность U=U (X, У) (рис. 5.22), то можно видеть, что муаровые полосы являются линиями уровня этой поверхности, т.е. линиями пересечения этой поверхности с горизонтальными плоскостями, расположенными на расстоянии 
одна от другой. Аналогично муаровые полосы, образованные сеткой линий, нанесенных в направлении оси X, являются линиями уровня поверхности 
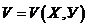. Обе картины муаровых полос дают полное представление о поле перемещений поверхности исследуемой детали.
Рис. 5.22. Геометрическая интерпретация картин муаровых полос
По картинам муаровых полос строят графики изменения U и V вдоль прямых, параллельных координатным осям. Кривые U(x,c) и 
(с, у) вдоль линий Х = С и У=С на рис. 5.22 являются примерами таких графиков. Из этих графиков определяют частные производные. Так, по кривой (х, с) на рис. 5.22 могут быть определены величины 
вдоль линии у = с, а по кривой U=U(c,y) величины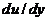 
вдоль линии х = с.
При численном дифференцировании дифференциалы должны быть заменены конечными приращениями, 
, 
V, Х и 
. В качестве Х и можно взять расстояние между соседними муаровыми полосами, измеренными в координатных направлениях. Тогда соответствующие им приращения 
и частные производные определятся из равенства:
, (5.54)
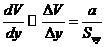
где - шаг недеформированного (эталонного) растра;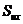 
, 
- расстояния между соседними муаровыми полосами на картине линий уровня U, измеренные в направлении осей х и y;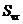 
, 
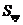- то же для картины линий уровня.
При построении графиков и V используются свойства непрерывности и единственности поля перемещений.
