При обработке результатов измерений широко используют методы графического изображения, которое дает более наглядное представление о результатах эксперимента, чем табличные данные. Поэтому сведенные в таблицы данные обрабатывают графическими методами. Для графического изображения используют обычно прямоугольную систему координат.
Прежде чем строить график, необходимо знать ход (течение) исследуемого процесса, что может быть известно, в частности, из теоретических исследований. Экспериментальные точки на графике необходимо соединять плавной линией, чтобы она по возможности ближе проходила ко всем экспериментальным точкам. Иногда исследуются явления, для которых в определенном интервале наблюдается скачкообразное изменение одной из координат, объясняемое сущностью физико-химического процесса. Если при построении графика появляются точки (одна – две), которые резко удаляются от плавной кривой, то необходимо проанализировать причину этого отклонения (грубая ошибка измерения или естественный ход процесса), а также повторить измерения в диапазонe резкого отклонения точки. Повторные измерения подтвердят или отвергнут (в случае грубой ошибки) наличие указанного отклонения. Если измеряемая величина В является функцией двух переменных параметров (
), то в одних координатах можно построить несколько графиков, разбив диапазон изменения одного из параметров на несколько отрезков (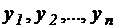
). При графическом изображении результатов экспериментов большую роль играет выбор системы координат (координатной сетке). Координатные сетки бывают равномерными и неравномерными.
Неравномерные сетки: полулогарифмические, вероятностные и др. применяют для более наглядного представления (изображения) изучаемой зависимости (спрямление криволинейных зависимостей и пр.).
При построении графиков (особенно расчетных) большое значение имеет выбор масштаба. Масштаб по координатным осям обычно применяют различный, что позволяет избежать слишком узких (высоких) или широких (низких) графиков. Графики с минимумом или максимумом необходимо особенно тщательно вычерчивать в области экстремума, поэтому здесь экспериментальные точки должны быть чаще.
Часто для систематических расчетов вместо сложных теоретических или эмпирических формул используют номограммы, которые строят, применяя равномерные или неравномерные координатные сетки. Последние предпочтительнее для спрямления графиков криволинейных функций.
