Расшифровка картин муаровых полос

Полученную в результате пластической деформации картину муа­ровых полос расшифровывают следующим образом.

Заснятую на пленку картину муаровых полос с помощью фотоуве­личителя проектируют в увеличенном (кратном) масштабе М 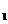, на миллиметровую бумагу. Остро заточенным карандашам проводят тонкие линии, совпадающие с центрами муаровых полос. Центр полосы опреде­ляют по местам наибольшего почернения.

После этого на увеличенную муаровую картину наносят координат­ную сетку сечений. Расстояние между линиями сетки, параллельными оси x-t, оси у- . Сечения, параллельные оси х, нумеруют 1,2,3,..., п, а параллельные оси у - I, 2', ,.... .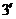

 

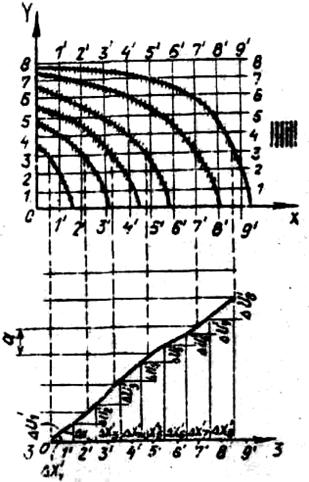
Рис. 5.23. Картина муаровых полос с нанесённой сеткой.

Линии растра перпендикулярны оси х

 

На рис. 5.23 представлена картина муаровых полос с нанесенной сеткой координатных сечений. Муаровые полосы в данном случае есть линии уровня поверхности (х, у). Пo картинам муаровых полос, представляю­щих собой линии уровня пере­мещений, строят графита изменения  и V вдоль прямых, параллельных координат­ным осям. Из этих графиков графическим дифференцированием определяют частные производные .

На нижней части рис. 5.23 представлена кривая изменения U вдоль сечения 3-3, по ко­торой определяют частные производные , как отношение приращения  на неко­тором участке к длине этого участка. Так, производная на участке (в точке) 3 опре­делится из выражения

,                                    (5.55)

где М₁ – масштаб увеличения муаровой картины; М₂ – масштаб увеличения поля эталонного растра.

Следует заметить, что построение графиков по всем сечениям реформируемого тела – трудоемкая операция. Поэтому для расшифровки картин муаровых полос частные производные вычисляют без построения графиков. Рассмотрим рис. 5.24, на котором представлен график изме­нения перемещения U вдоль неко­торого сечения, параллельного оси X. Требуется вычислить  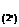ячейки 2. Из рис. 5.24 следует, что

Так как , а ; , получим

                        (5.56)

где  - расстояния между соседними муаровыми полосками в направлении оси х;  - длина ячейки на которой определяется приращение , а – шаг эталонной решетки, умноженный на М₁.

Если в размер ячейки попадает N полюс, а не 2, как на рис 5.24, то для данной ячейки получим

.

Величины с, d, R₁ и Z_n+2 находят непосредственно на миллиметровой бумаге, на которую спроектирована картина муаровых полос, а вместо величины 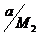подставляют шаг эталонного раствора без увеличения.

Так как картина муаровых полос характеризует распределение перемещений в деформированном состоянии тела, то определенные по ней перемещения U и V соответствуют координации Эйлера. Переход к более употребительным координатам Лагранжа осуществляется по формулам:

;

; .                      (5.57)

Подставив значения производных из Х, получим формулы для вычисления относительных деформаций (Лангранжевых):

.

Если величины  и 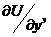не превышают величины 0,3 (что обычно имеем на практике), то в выражении (5.57) им можно пренебречь. Погрешность при этом не превышает 5 %. Кроме того, в случае плоской деформации значения производных  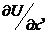и  имеют равные знаки и незначительно отличаются по величине, поэтому можно считать

                                          (5.74)

С учетом указанного выражения (5.57) упростятся и будут иметь вид:

.

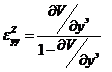
Из теории пластичности известно, что при плоской деформации , поэтому в принципе достаточно определить и . По известным значениям и находят интенсивность пластических деформаций из выражения

По распределению в швах, в предложении о единой кривой течения, определяют распределение интенсивности напряжений в пластической стадии деформирования швов.

 

Рис. 5.24. Изменение перемещения U вдоль се­чения, параллельного

оси X