Метрология – наука об измерениях, методах достижения их единства и требуемой точности.
Измерение – процесс нахождения какой-либо физической величины опытным путем с помощью специальных технических средств. Это процесс сравнения величины чего-либо с известной величиной, принятой за единицу (эталон).
Измерения бывают статическими, когда измеряемая величина не изменяется во времени, и динамическими, когда измеряемая величина меняется.
Измерения разделяются на прямые к косвенные. При прямых – искомую величину устанавливают непосредственно из опыта, при косвенных – функционально от других величин, определенных прямыми измерениями (например, плотность тела через массу к объем).
Различают также абсолютные и относительные измерения. Абсолютные – это прямые измерения в единицах измеряемой величины. Относительные – измерения, представленные отношением измеряемой величины к одноименной величине, принимаемой за сравнимую. Различают три класса измерений: особо точные, высокоточные и технические.
Измерения являются основной составной частью любого эксперимента. От их тщательности зависят результаты эксперимента. Поэтому каждый экспериментатор должен знать закономерности измерительных процессов; уметь правильно измерит отучаемые величины; оценить погрешности при измерениях; правильно, с требуемой точностью вычислить значения величия и их потребное минимальное количество; определить наилучшие условия измерений, при которых ошибки будут наименьшими, и произвести общий анализ результатов измерений.
Точность измерения – это степень приближения измерения к действительному значению измеряемой величины.
Погрешность измерения – это алгебраическая разность между действительным значением измеряемой величины и полученным при измерении.
Необходимое минимальное количество измерений – это такое количество, которое обеспечивает устойчивое среднее значение измеряемой величины, удовлетворяющее заданной степени точности. Чтобы повысить точность и достоверность измерений, необходимо уменьшить погрешности. Погрешности при измерениях возникают вследствие ряда причин: несовершенства методов и средств измерений, недостаточно тщательного проведения опыта, влияния различных внешних факторов в процессе опыта, субъективных особенностей экспериментатора и др. Погрешности бывают систематическими и случайными.
Систематические – такие погрешности измерений, которые при повторных опытах остаются постоянными (или изменяются по известному закону). Если численные значения этих погрешностей известны, их можно учесть во время повторных измерений.
Случайные – возникают чисто случайно при повторном измерении. Их нельзя учесть и исключить. Однако при многократно повторенных измерениях с помощью статистических методов наиболее отклоняющиеся случайнее измерения (погрешности) можно исключить.
Систематические погрешности можно разделить на 5 групп:
1) инструментальные – из-за износа и люфтов, неточности градуировочной шкалы идр.;
2) неправильная установка средств измерения;
3) влияние внешней среды: магнитных или электрических полей, высоких или низких температур, влажности, вибрации и др.;
4) субъективные;
5) методические – обоснованные выбором метода измерений.
От систематических погрешностей 1, 2, 3 и 5 групп можно избавиться до начала эксперимента.
Согласно теории случайных ошибок:
1. При большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;
2. Большие погрешности встречаются реже, чем малые;
3. При бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений;
4. Появление того или иного результата измерения как случайного события описывается нормальным законом распределения, если число измерений больше 30, или распределением Стьюдента, если количество измерений меньше 30.
5. Считается, что при числе измерений больше 30 среднее значение данной совокупности измерений достаточно приближается к истинному.
Теория случайных ошибок позволяет решить 2 задачи: оценить точность и надежность измерений при данном количестве замеров; определить минимальное количество замеров, гарантирующее заданную точность измерения.
Точность измерений:
 . (4.1)
. (4.1)
где  – средняя ошибка измерений;
– средняя ошибка измерений;
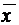 – среднее значение некоторого числа измерений;
– среднее значение некоторого числа измерений;
Минимальное количество измерений:
 . (4.2)
. (4.2)
 – коэффициент вариации, равный
– коэффициент вариации, равный  ;
;
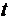 – гарантийный коэффициент (0 £
– гарантийный коэффициент (0 £ 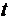 £ 4);
£ 4);
 – дисперсия (рассеяние-отклонение от среднего), определяется по уравнению
– дисперсия (рассеяние-отклонение от среднего), определяется по уравнению  .
.
 – число измерений.
– число измерений.
Задаваясь гарантийным коэффициентом определяют доверительный интервал по формуле:
 (4.3)
(4.3)
и доверительную вероятность 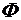 по таблицам. При изменении t от 0 до 4
по таблицам. При изменении t от 0 до 4 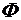 изменяется от 0 до 0,9999.
изменяется от 0 до 0,9999.
Оценка измерений с помощью  и
и  по уравнениям (4.1), (4.2) справедлива при
по уравнениям (4.1), (4.2) справедлива при  .
.
При  применяют метод Стьюдента (псевдоним английского математика В. Госсета).
применяют метод Стьюдента (псевдоним английского математика В. Госсета).
Доверительный интервал:
 , (4.4)
, (4.4)
где 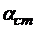 – коэффициент Стьюдента. Определяется по таблицам в зависимости от числа опытов и доверительной вероятности.
– коэффициент Стьюдента. Определяется по таблицам в зависимости от числа опытов и доверительной вероятности.
Средства измерений
Средства измерений – совокупность технических средств, используемых при изменениях и имеющих нормированные метрологические характеристики. Они являются неотъемлемой частью эксперимента и дают нам необходимую информацию. К средствам измерения относят измерительные инструменты, приборы и установки. Измерительные средства делят наобразцовые и технические.
Образцовые – являются эталонами и предназначены для проверки технических (рабочих) средств. Они не обязательно точнее рабочих, но должны иметь большую стабильность и надежность в воспроизведении измерения, Образцовые средства не применяют для рабочих измерений.
По характеру участия в процессе измерения все средства можно разделить на меры, измерительные преобразователи, измерительные приборы и измерительные (измерительно-информационные) системы.
Мера – средство измерений, предназначенное для воспроизведения физической величины данного размера. Меры бывают однозначные, многозначные и наборы Однозначные меры – гири, размерные плитки, конденсаторы постоянной емкости и др. Многозначные – конденсатор переменной емкости, проволочный реохорд и др. Наборы состоят из однозначные мер.
Измерительный преобразователь – средство измерений, предназначенное для выборки сигнала измерительной информации в форме удобной для передачи, обработки и хранения, но не поддающейся непосредственному восприятию наблюдателем. К измерительным преобразователям относятся датчики (термопары, тензорезисторы и др.), усилители.
Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем.
Измерительно-информационные системы – совокупность технических средств в блочно-модульном исполнении, объединенных общим алгоритмом функционирования, обладающие нормированными метрологическими характеристиками и предназначенные для получения измерительной информации непосредственно от объекта, ее преобразования, передачи, хранения, обработки и выдачи в виде, удобном для восприятия оператором или ввода в систему автоматического управления.
По способу отсчета значения измеряемой величины приборы делятся на показывающие и регистрирующие. Показывающие – аналоговые (шкала и стрелка) и цифровые. Регистрирующие – самопишущие и печатные. Самопишущие выдают график изменений, печатные – последовательность цифр на ленте.
Измерительные приборы характеризуются величиной погрешности и точности, стабильности измерений и чувствительностью.
Погрешность – одна из важных характеристик прибора. Различают абсолютную и относительную погрешность.
Абсолютная –  , (4.5)
, (4.5)
относительная –  %, (4.6)
%, (4.6)
где  – показание прибора (номинальное значение измеряемой величины);
– показание прибора (номинальное значение измеряемой величины); 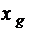 – действительное значение измеряемой величины, полученное более точным методом.
– действительное значение измеряемой величины, полученное более точным методом.
Точность – основная характеристика прибора. Характеризуется суммарной (основной) погрешностью. В зависимости от допустимой погрешности приборы делят на классы. Часто класс точности обозначаю допускаемой погрешностью в % (1, 2 и т. п.).
Стабильность – свойство отсчетного устройства прибора обеспечивать постоянство показаний одной и той же величины. Стабильность определяется вариацией показания (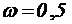 ). Средства измерений подвергаются поверке через каждые 1 – 2 года.
). Средства измерений подвергаются поверке через каждые 1 – 2 года.
Планирование эксперимента
Чтобы производить эксперимент в наиболее короткий срок и с наименьшими затратами, получая при этом достоверную информацию, необходимо планирование. Этого можно достигнуть, следуя при планировании определенным правилам, учитывающим вероятностный характер результатов измерений и наличие внешних помех, воздействующих на изучаемый объект.
При планировании все факторы, определяющие процесс, изменяются одновременно по специальным правилам, а результаты эксперимента представляется в виде математической модели, обладающей некоторыми статистическими свойствами.
Выделяют следующие этапы планирования:
- сбор и анализ априорной информации;
- выбор входных ивыходных переменных, области экспериментирования (изменения переменных);
- выбор математической модели с помощью которой будут представляться экспериментальные данные;
- выбор критерия оптимальности и плана эксперимента;
- определение метода анализа данных;
- проведение эксперимента;
- проверка статистических предпосылок для подученных и ментальных данных;
- обработка результатов;
- рекомендации.
В процессе сбора и анализа априорной информации устанавливают и анализируют известные данные об изучаемом объекте: какие факторы и как влияет на его состояние, возможные пределы изменения этих факторов, их взаимосвязь и др.
Основное требование при выборе входных факторов (переменных) – возможность установления нужного значения (уровня) этого фактора и поддержание его в течение всего опыта. Факторы могут быть количественными и качественными. Уровням количественных факторов соответствует числовая шкала (температура, давление и т. д.).
Выходные переменные – реакции (отклики) на воздействие входных параметров. Могут быть экономическими (расход энергии, прибыль и т.п.), технологическими (стабильность горения дуги, надежность и т.п.) и т.д.
Выбор модели зависит от наших знаний об объекте, целей исследования и математического аппарата. Очень часто исследовательские задачи сводятся к задаче получения статистической модели, которая представляет собой математическую зависимость между выходными и входными параметрами изучаемого объекта. Теоретической основой решения задачи статистического моделирования является предположение о возможности описания протекающего процесса системой дифференциальных уравнений. Но если из-за слабой изученности и сложности процесса это осуществить невозможно, то предполагаемое решение этих уравнений можно разложить в ряд Тейлора по переменным параметрам. Наиболее часто используют многочлен первой степени, являющийся самой простой формой статистической модели объекта, а именно:
 , (4.7)
, (4.7)
где  – выходной параметр;
– выходной параметр;  – входные параметры;
– входные параметры;  – коэффициенты многочлена, определяемые на основе экспериментальных данных статистическим анализом.
– коэффициенты многочлена, определяемые на основе экспериментальных данных статистическим анализом.
Обработка экспериментальных данных сводятся к отыскиванию коэффициентов многочлена по известным из опытов данным 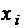 и
и  .
.
Для этого надо составить  уравнение, и следовательно, надо провести не менее
уравнение, и следовательно, надо провести не менее  опыт, чтобы вкаждом из ниx значения входных параметров
опыт, чтобы вкаждом из ниx значения входных параметров 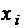 составляли свою, отличную от других опытов комбинацию. Тогда и выходные параметры u
составляли свою, отличную от других опытов комбинацию. Тогда и выходные параметры u  будут во многих опытах различными.
будут во многих опытах различными.
Чтобы уменьшить общий объем вычислений и упростить сам эксперимент, нужно каждый входной параметр варьировать только на двух уровнях: нижнем (-1) и верхнем (+1). В этом случае для нахождения коэффициентов регрессии, например при трех входных параметрах, необходимо провести лишь четыре опыта по плану (матрице планирования), приведённому в таблице 4.1.
Таблица 4.1
| № опыта | План | Результат эксперимента | ||

| 
| 
| ||
| 1 | -1 | -1 | +1 | 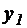
|
| 2 | +1 | -1 | -1 | 
|
| 3 | -1 | +1 | -1 | 
|
| 4 | +1 | +1 | +1 | 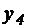
|
Коэффициенты регрессии при использовании такого плана можно рассчитать по формуле:
 , (4.8)
, (4.8)
где  – номер входного параметра и соответствующего ему коэффициента регрессии;
– номер входного параметра и соответствующего ему коэффициента регрессии; 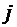 – номер опыта;
– номер опыта;  – число опытов;
– число опытов;  – уровень параметра
– уровень параметра 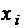 в
в 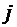 -м опыте (+1 или -1);
-м опыте (+1 или -1); 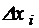 – отклонение параметра
– отклонение параметра 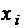 от исходного значений (основного уровня) – интервал варьирования.
от исходного значений (основного уровня) – интервал варьирования.
Коэффициент  определяют по формуле:
определяют по формуле:
 , (4.9)
, (4.9)
где  – число входных параметров.
– число входных параметров.
Для выявления возможного взаимодействия входных параметров необходимо осуществить полный факторный эксперимент по плану (для трех факторов), приведенному в таблице 4.2.
Таблица 4.2
| № опыта | 
| 
| 
| 
| 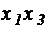
| 
| 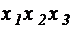
| 
|
| 1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | 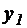
|
| 2 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | 
|
| 3 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | 
|
| 4 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | 
|
| 5 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | 
|
| 6 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | 
|
| 7 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | 
|
| 8 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | 
|
В этом случае регрессии будут иметь вид:
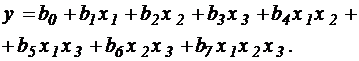 (4.10)
(4.10)
Соответствие формы уравнения регрессии исследуемому объекту проверяют по дисперсии адекватности:
 , (4.11)
, (4.11)
где 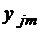 и
и  – значения выходного параметра, рассчитанные по статистической модели и полученные при дополнительных опыта; k - число дополнительных шагов.
– значения выходного параметра, рассчитанные по статистической модели и полученные при дополнительных опыта; k - число дополнительных шагов.
Опыты по определению дисперсии адекватности следует проводить при различных значениях входных параметров.
Для проверки адекватности модели часто используют F – критерий Фишера
 , (4.12)
, (4.12)
где
 , (4.13)
, (4.13)
 – значение выходной величины
– значение выходной величины 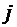 - го опыта;
- го опыта; 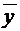 – среднее значение выходной величины (параметра).
– среднее значение выходной величины (параметра).
Определенное по формуле значение  сравнивают с табличным
сравнивают с табличным  . Если
. Если  , то с доверительной вероятностью модель можно считать адекватной изучаемому процессу. Если линейная модель неадекватна, то следует перейти к модели более высокой степени – уравнению регрессии второго порядка.
, то с доверительной вероятностью модель можно считать адекватной изучаемому процессу. Если линейная модель неадекватна, то следует перейти к модели более высокой степени – уравнению регрессии второго порядка.
Часто задачей исследования является оптимизация процесса, т.е. определение таких значений входных параметров, для которых выходкой параметр имеет максимальное или минимальное значение. В решении такой задачи можно выделить два подхода. Первый – создание теории процесса (математической модели), с помощью которой определяют оптимальные условия. Второй – эмпирический. Существует и промежуточный подход, когда вид исходной модели определяется теоретическими представлениями, а значения параметров рассчитывают по экспериментальным данным, полученным при изучении объекта.
Эмпирический подход в последние десятилетия используется все шире, что объясняется ростом сложности изучаемых объектов, недостатком времени на их детальное изучение и появлением новых эмпирических способов оптимизации и др. К числу таких новых способов принадлежат методы Бокса - Уилсона и симплекс-планирования. Бокс и Уилсон предложили метод крутого восхождения – движение по градиенту отдельными шагами до тех пор, пока не будет достигнут оптимум.






