1. Построение матриц. Матрицы можно задавать различными способами. До сих пор использовались два способа: кнопкой Вставить матрицу или с помощью индексов, заданных ранжированной переменной. Ниже перечислены другие возможности.
| Задание необходимых индексов |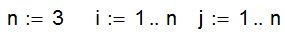 
|
| Легко задается матрица, компоненты которой есть функция от индексов. | 
|
| Матрица, состоящая из одинаковых чисел, задается присваиванием этого числа каждому элементу матрицы. | 
|
| Аналогично задается только строка или столбец матрицы. | 
|
Единичную матрицу размера  можно задать функцией identity(n) или присваивая единицу элементам главной диагонали.
| 
|
| Диагональную матрицу с вектором v1 на диагонали можно получить, применив функцию diag(v1). | 
|
| Чтобы «повернуть» матрицу на 90 градусов по часовой стрелке нужно задать второй индекс в обратном порядке. | 
|
| Для заполнения побочных диагоналей матрицы нужно сместить один индекс на единицу: k:=1..n–1. | 
|
2. Построение блочных матриц. Функции augment и stack позволяют легко строить т. н. блочные матрицы из матриц (блоков) меньших размеров. Например, пусть даны матрицы
.
Из них можно составить блочную матрицу 
. Один из способов построения показан на рис. 36
Рис. 36. Построение блочной матрицы
3. Функции, вычисляющие по матрице число. Часто такие функции можно рассматривать как последовательное применение двух функций: первая вычисляет по матрице одномерный массив, вторая по массиву — число.
Рассмотрим получение вектора из матрицы подробно.
| 
|
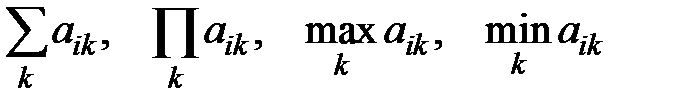
| В каждом из этих случаев столбец — второй индекс (здесь j, а может быть любая буква) фиксирован, а суммирование (произведение, поиск максимума или минимума) осуществляется по строке — первому индексу (здесь k, или любая другая буква) для каждого столбца. В результате получается вектор с количеством элементов равным количеству столбцов. | В каждом из этих случаев строка — первый индекс (здесь i, а может быть любая буква) фиксирована, а суммирование (произведение, поиск максимума или минимума) осуществляется по столбцу — второму индексу (здесь k, или любая другая буква) для каждой строки. В результате получается вектор с количеством элементов равным количеству строк. |
Поиск максимума и минимума производится функциямиmax и min.Знаки суммы и произведения вводятсячерез панель «Мат. анализ» (Culculus) с помощью кнопок 
, 
, 
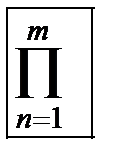и 
(подробнее см. §27).
Рассмотрим вычисление вектора 
. Нужно вычислить максимум по всем k при фиксированном j. Другими словами, для каждого столбца j нужно найти максимальный элемент. Столбец выделяется кнопкой 
.Если нужно вычислить 
— максимальный элемент в строке i, — то для строки кнопки нет. Нужно строку сделать столбцом, т. е. транспонировать (рис. 37).
Рис. 37. Максимум от элементов матрицы
ЗАДАНИЕ А
Построить заданную матрицу, применяя изученные способы.
