ЗАДАНИЕ и ВАРИАНТЫ
Выполнить задание работы 2_1 (стр. 15) по вариантам (стр. 18–19).
ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ
Пусть задана функция 
1. Задать функции y1(x), y2(x), y3(x) — это упростит выражения.
2. Вектор аргументов х не задавать.
3. Задать функцию f (x). Соответствующая блок-схема (рис. 39) реализуется в Mathcad функцией
if(<условие>, f1, f2),
которая равна функции f1, если <условие> истинно, и функции f2 в противном случае. Нужно записать два условия, поэтому
if(<условие_1>, f1, if(<условие_2>, f2, f3))

Рис. 39. Блок-схема для вычисления функции f (x)
Знаки отношения — больше, больше или равно и т. д. — вводятся через панель Логические операторы. Аргументы функции if разделяются запятыми. Сравнить функцию if с функцией ЕСЛИ в Excel, найти совпадения и различия.
4. Построить график. Задать на графике границы изменения переменной x, добавить сетку. Сравнить с графиком, построенным в Excel.
5. Продолжить Отчет 2. Графика и исследование функций. Часть 1. График кусочно-заданной функции.
5.1. В разделе 2. Результаты под подзаголовком Mathcad вставить результаты с комментариями.
РАБОТА 7_2. Решение уравнения и поиск экстремумов
ЗАДАНИЕ и ВАРИАНТЫ
Выполнить задание из работы 2_2 (стр. 19) по вариантам (стр. 22). Найти точки экстремумов (не менее трех) заданной функции.
ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ
1. Задать точность TOL через меню Инструменты (Tools) — Параметры документа (WorksheetOptions) — Встроенные переменные (Built-InVariables) или определить переменнуюTOL на рабочем листе, например, TOL:=0.0001.
2. Задать функцию y (x).
3. Построить график, не задавая вектор аргументов х. Меняя границы изменения аргумента, получить «хороший» график, на котором видны все корни (рис. 40). Для каждого корня по графику определить отрезок, на котором он содержится. При необходимости, сделать несколько графиков.
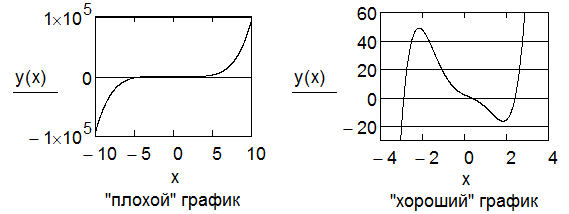
Рис. 40. «Плохой» и «хороший» графики
4. Найти корни — по одному. Для поиска корней в Mathcad существует функция root(y(x0),x0), где x0 и y(x0) — имя переменной и функция, корень которой ищется, от ЭТОЙ переменной. Причем переменная должна иметь начальное значение, близкое к корню.
4.1. Задать приближенное значение первого корня x01, пользуясь графиком.
4.2. Уточнить корень по формуле x1=root(y(x01),x01).
4.3. Сделать проверку подстановкой найденного корня в уравнение. В результате должно получиться число близкое к нулю.
4.4. Если корней несколько, поочередно уточнить значение каждого корня.
Сравнить с результатами, полученными в Excel.
5. Найти максимум функции. Для поиска локальных экстремумов имеются две функции: Maximize(y,x) и Minimize(y,x). Здесь y — имя (только!) оптимизируемой функции, x — аргумент, по которому производится оптимизация. Предварительно аргументу x нужно присвоить значение.
5.1. Задать приближенное значение координаты точки максимумаx03, найденной по графику.
5.2. Уточнить точку максимума по формуле х03:=Maximize(у,x03).
5.3. Найти значение функции в точке максимума.
5.4. Уточнить координаты минимума аналогично.
6. Продолжить Отчет 2. Графика и исследование функций. Часть 2. Исследование функции.
6.1. В раздел 1. Задание под подзаголовком Mathcad дописать задание про экстремумы.
6.2. В разделе 2. Результаты под подзаголовком Mathcad вставить результаты с комментариями.






