Для заданных матриц (рис. 18) вычислить значение выражения 
.
Рис. 18. Образец работы для выражения
1. Разбить выражение на простые блоки, содержащие одно-два действия
2. Ввести заголовки (рис. 18).
3. Ввести матрицы A, B и C и задать имена соответствующим диапазонам.
4. Вычислить выражение, последовательно вычисляя и задавая имена для каждого блока.
5. Создать Отчет 3. Работа с массивами. Часть 1. Матричные выражения
5.1. В разделе 1. Задание написать задание, вводя матрицы и формулы.
5.2. В разделе 2. Результаты под подзаголовком Excel написать, как делать матричные вычисления:
– что надо сделать, прежде чем ввести формулу;
– как вводить матрицу и формулы;
– что надо сделать, после ввода формулы.
5.3. Экспортировать результаты в Word.
ВАРИАНТЫ
Задать матрицы
| 
| 
|
и найти значения следующих выражений:
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 
|
ЗАДАНИЕ Б
Вычислить значения заданной функции для каждого элемента матрицы.
Указания. По смыслу задания умножение здесь поэлементное, следовательно, выполняется, как обычное умножение. В сложных случаях можно разбить выражение на блоки и производить вычисления по частям.
ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ
Для каждого элемента матрицы 
вычислить значение функции 
.
1. Ввести заголовки (рис. 19).
2. Ввести матрицу-аргумент и задать имя для этого диапазона.
Рис. 19. Образец работы
3. Вычислить значения выражения. Выделить диапазон ячеек необходимый для результата (размером с матрицу-аргумент), ввести формулу и нажать {Ctrl+Shift+Enter}.
4. Сделать проверку. Ввести формулу со ссылкой на первую ячейку матрицы-аргумента и растянуть ее вправо-вниз маркером автозаполнения. Сравнить полученные результаты.
5. Продолжить Отчет 3. Работа с массивами. Часть 2. Поэлементные операции над матрицами.
5.1. В разделе 1. Задание написать задание, вводя матрицы и формулы.
5.2. В разделе 2. Результаты под подзаголовком Excel написать, как производить поэлементные операции над матрицами. В чем отличие от матричных вычислений.
5.3. Экспортировать результаты в Word.
ВАРИАНТЫ
| 1. | 
| 
|
| 2. | 
| 
|
| 3. | 
| 
|
| 4. | 
| 
|
| 5. | 
| 
|
| 6. | 
| 
|
| 7. |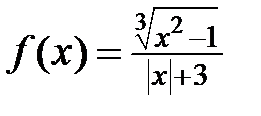 
| 
|
| 8. | 
| 
|
| 9. | 
| 
|
| 10. | 
| 
|
| 11. | 
| 
|
| 12. | 
| 
|
| 13. | 
| 
|
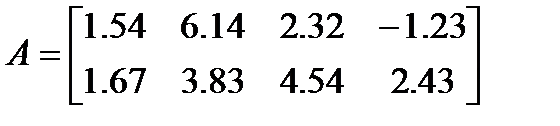
| 14. | 
| 
|
РАБОТА 3_4. Решение СЛАУ
ЗАДАНИЕ
Для данной системы линейных алгебраических уравнений (СЛАУ) 4-ого порядка найти определитель матрицы системы, вычислить обратную матрицу, найти решение и сделать проверку, вычислив невязку.
ПРЕДВАРИТЕЛЬНАЯ ИНФОРМАЦИЯ
Дана СЛАУ
.
Если ввести обозначения для матрицы коэффициентов A, вектора неизвестных x и вектора свободных членов b
, 
, 
,
тогда СЛАУ можно записать в матричном виде 
. Из математики известно, решение СЛАУ существует и единственное, если определитель матрицы системы не равен нулю. Из этого также следует существование обратной матрицы 
:
.
Тогда решение системы находится умножением обеих ее частей слева на обратную матрицу.
.
Чтобы проверить, правильно ли найдено решение, можно подставить найденное решение x в исходную систему и вычислить разность правой и левой частей — так называемую невязку. Если решение вычислено точно, то невязка 
, если приближенно — близка к нулю.
