ЗАДАНИЕ и ВАРИАНТЫ
Выполнить задание из работы 1_2 (стр. 11–12) по вариантам (стр. 14–15).
Указание: Все результаты должны совпадать с результатами работы 1_2, соответственно должны совпадать и все исходные данные. При получении другого результата нужно искать ошибку (возможно в работе 1_2).
ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ
1. Установить 4 десятичных знака в меню «Format» — «Result…» на вкладке NumberFormat (для удобства сравнения результатов с Excel).
2. Задать параметры a и b. Если нужно, то c и d (рис. 30).
3. Ввести функцию двух переменных f (x, y).
Рис. 30. Образец работы
4. Задать х, у, и получить значение функции f (x, y). Сверить с результатами в Excel и, если необходимо, исправить ошибки.
5. Задать вторую пару х, у, и получить новое значение функции f (x, y).
6. Задать ранжированную переменную х.
7. Задать у, и вывести столбец значений f (x, y). Повторить еще для двух значений переменной y.
Замечание: вспомнить последовательность выполнения команд слева направо сверху вниз. Проследить за тем, чтобы столбцы f (x, y) каждый раз выводились для нового значения y.
8. Задать новые значения параметров a и b (c и d) и вывести столбец значений f (x, y), не задавая снова значений х и у (т. е. для столбца х и последнего у).
Замечание: чтобы в функции отразились изменения параметров см. п. 2.6.
9. Продолжить Отчет 1. Вычисление значений функции с параметрами.
9.1. В разделе 2. Результаты под подзаголовком Mathcad прокомментировать приемы ввода СВОЕЙ формулы. Написать, что такое и как задается ранжированная переменная. Объяснить, почему в последней части работы пришлось снова вводить формулу, а для получения результатов при изменении аргументов этого не делали. Вставить выполненную работу.
Вектора и матрицы
1. Определения. Матрица размера 
— таблица чисел, состоящая из m строк и n столбцов. Матрицы, у которых один размер равен единице называют вектор-столбцом (
) или вектор-строкой (
).
Внимание. Вектором в математическом смысле является вектор-столбец. Вектор-строка — это просто матрица 
.
Везде ниже вектор — это вектор-столбец, строка — это вектор-строка (рис. 31).
Рис. 31. Матрицы и вектора
2. Ввод матриц и векторов. Матрицы и вектора вводятся через панель Матрицы первой кнопкой Вставить матрицу. При этом открывается окно работы с матрицами, в котором можно задать число строк (Rows) и число столбцов (Columns).
3. Работа с элементами матриц и векторов. Расположение элементов матрицы задается нижним индексом: первый индекс — номер строки, второй — столбца. Для вектора можно не указывать вторую единицу (рис. 32). Нижние индексы вводятся посредством кнопки 
(Subscript) или горячей клавишей 
.
Рис. 32. Строка и вектор
4. Переменная ORIGIN определяет начало нумерации индексов. По умолчанию 
, что неудобно при работе с матрицами (рис. 33). Изменить начало нумерации можно через меню Инструменты (Tools) — Параметры документа (WorksheetOptions…) — Встроенные переменные (Built-InVariables) или присваиванием в начале листа 
.
Рис. 33. Начало нумерации
Внимание. Первой строкойв работе с векторами и матрицами рекомендуется (если нет причин, по которым удобно работать с нулевым индексом) изменить начало нумерации на единицу: ORIGIN:=1.
5. Ранжированная переменная — это особая разновидность вектора, предназначенная для создания циклов и итерационных вычислений. Это вектор, с которым работают как с числом. Ранжированные переменные удобно использовать при построении векторов и матриц (рис. 34)
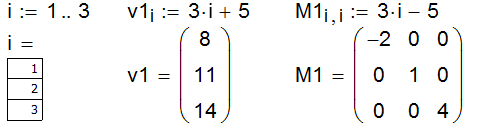
Рис. 34. Ранжированная переменная
6. Операции и функции над векторами и матрицами
6.1. Сложение, вычитание и умножение на число. Складывать и вычитать можно матрицы и вектора одинаковых размеров.
6.2. Произведение векторов и матриц. Скалярное произведение векторов (сумма произведений элементов) и произведение матриц производятся обычным знаком умножения. У векторов и матриц при этом должны совпадать соответствующие размеры. Для векторов с тремя компонентами определено векторное умножение — кнопка 
на панели «Матрицы».
6.3. Векторные функции — можно использовать только для векторов.
| length(a) | количество элементов вектора a |
| last(a) | индекс последнего элемента вектора a |
| sort(a) | сортировка по возрастанию элементов вектора a |
| reverse(a) | перестановка элементов вектора a в обратном порядке |
Замечание. Чтобы применять векторные операции к строке надо строку транспонировать (кнопка 
на панели Матрицы).
6.4. Матричные функции.
| rows(M) | количество строк матрицы M |
| cols(M) | количество столбцов матрицы M |
| max(M1,M2) | максимальный элемент нескольких матриц |
| min(M1,M2) | минимальный элемент нескольких матриц |
| augment(M1, M2) | соединение нескольких матриц слева направо (при одинаковом числе строк) |
| stack(M1, M2) | соединение нескольких матриц сверху вниз (при одинаковом числе столбцов) |
6.5. Операции над матрицами с панели инструментов «Матрицы».
Производя различные действия с матрицами и векторами нужно учитывать соответствие размеров.
| Обратная матрица | 
| только для квадратных матриц с ненулевым определителем |
| Определитель | 
| только для квадратных матриц (в отличие от модуля) |
| Обращение к столбцу матрицы | 
| бессмысленно для вектора |
| Транспонирование | 
| строки становятся столбцами и наоборот |
| Сумма элементов | 
| только для векторов и строк |
6.6. Поэлементные действия — кнопка векторизация 
на панели «Матрицы». Все действия под стрелкой выполняются поэлементно, т. е. для каждого элемента матрицы (рис. 35.)
Рис. 35. Векторизация
