Раздел 1 Теория вероятностей
Тема 1.1 Основные понятия теории вероятностей
1.1.1 Стохастический эксперимент.
1.1.2 Случайные явления и случайные события.
1.1.3 Некоторые классические модели.
Возникновение теории вероятностей относят к XVII веку и связывают с решением комбинаторных задач теории азартных игр и потребностями страхового дела. Азартные игры и страхование являются классическими примерами вероятностных экспериментов. Именно азартные игры дали стимул для построения математических моделей игровых ситуаций. Эти модели предоставляли возможность игроку ориентироваться в ходе игры, делать расчет ставок, оценивать шансы выигрыша, а также позволяли планировать расходы и доходы страховых компаний и т.д.
Эти модели начали разрабатывать в XVII веке Б.Паскаль, П.Ферма, Х.Гюйгенс. Основы классической теории вероятностей, которые сохранились и в настоящее время, были сформулированы в XVIII веке в работах Я.Бернулли, А.Муавра, П.Лапласа, С.Пуассона, К.Гаусса.
В 1933 г А.Н.Колмогоров опубликовал «Основные понятия теории вероятностей», в которой дал аксиоматическое построение теории вероятностей, основанной на теории множеств. Такое построение теории вероятностей сделало ее строгой математической наукой.
В это же время выделяется новая дисциплина—математическая статистика, которая имеет в настоящее время огромное прикладное значение. Она применяется в экономике, технике, социологии, физике и т.д. От ТВ отделились новые математические дисциплины: теория случайных процессов, теория массового обслуживания, теория планирования экспериментов. Сейчас они бурно развиваются.
Стохастический эксперимент.
Вероятностный эксперимент. Предмет и задачи теории вероятностей.
Результаты любого эксперимента в той или иной степени зависят от комплекса условий S, при которых данный эксперимент производится. Эти условия либо объективно существуют, либо создаются искусственно (т.е. производится планирование эксперимента).
По степени зависимости результатов эксперимента от условий, при которых он производился, все эксперименты можно разделить на два класса: детерминированные и вероятностные.
o Детерминированные эксперименты - это эксперименты, результаты которых можно предвидеть заранее на основании естественнонаучных законов исходя из данного комплекса условий S.
Примером детерминированного эксперимента является определение ускорения, получаемого телом массы m под воздействием силы F, т.е.. Искомая величина однозначно определяется комплексом условий эксперимента (т.е.  массой тела m и силой F).
массой тела m и силой F).
Детерминированными являются, например, все процессы, основанные на использовании законов классической механики, согласно которым движение тела однозначно определяется заданными начальными условиями и силами, действующими на тело.
o Вероятностные эксперименты (стохастические или случайные) — эксперименты, которые можно повторять произвольное число раз при соблюдении одних и тех же стабильных условий, но, в отличие от детерминированного, исход вероятностного эксперимента неоднозначен, случаен. Т.е. нельзя заранее на основании комплекса условий S предвидеть результат вероятностного эксперимента. Однако, если вероятностный эксперимент повторять многократно при одних и тех же условиях, то совокупность исходов таких экспериментов подчиняется определенным закономерностям. Изучением этих закономерностей (а точнее их математических моделей) и занимается теория вероятностей. Приведем несколько примеров вероятностных экспериментов, которые в дальнейшем будем называть просто экспериментами.
Пример 1
Пусть эксперимент заключается в однократном подбрасывании симметричной монеты. Этот эксперимент может закончиться одним из исключающих друг друга исходов: выпадение герба или решетки (решки). Если точно знать начальные скорости поступательного и вращательного движения и начальное положение монеты в момент броска, то можно предвидеть результат этого эксперимента по законам классической механики. Т.е. он был бы детерминированным. Однако исходные данные эксперимента не могут быть зафиксированными и постоянно изменяются. Поэтому говорят, что результат эксперимента неоднозначен, случаен. Тем не менее, если будем подбрасывать одну и ту же симметричную монету многократно по достаточно длинной траектории, т.е. по возможности сохраним стабильными некоторые условия эксперимента, то совокупное число его исходов подчиняется определенным закономерностям: относительная частота выпадения герба 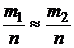 , частоте выпадение бросков (n—число бросков, m1—число выпадений герба, m2—решки).
, частоте выпадение бросков (n—число бросков, m1—число выпадений герба, m2—решки).
Пример 2
Предположим, что мы заполняем карточку спортлото. До проведения тиража выигрышей невозможно предсказать, сколько номеров будет правильно угадано. Однако опыт проведения тиража спортлото говорит о том, что средний процент игроков, угадавших m (1≤m≤6) номеров, колеблется около некоторой постоянной величины. Эти «закономерности» (средний процент правильного угадывания данного количества номеров) используются для расчета фондов выигрыша.
Вероятностные эксперименты имеют следующие общие черты: непредвиденность результата; наличие определенных количественных закономерностей при их многократном повторении при одинаковых условиях; множество возможных исходов.
o Предметом теории вероятностей является количественный и качественный анализ математических моделей вероятностных экспериментов, называемый статической обработкой экспериментальных данных.
o Теория вероятностей — наука, занимающаяся анализом математических моделей для принятия решений в условиях неопределенности.






