Определение. Суммой событий А 1, А 2, …, А n называется такое событие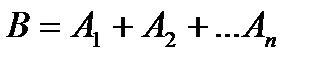 
, которое состоит в том, что произошло хотя бы одно из событий А 1, А 2, …, А n .
Пример1. Событие А – появление 3 очков, а В – появление 6 очков при одном бросании игральной кости, тогда А+В – это появление или 3 или 6 очков, т.е. числа очков, кратного трем.
Пример 2. Произведено 3 выстрела по мишени. Введем такие события:
- ни одного попадания;
- одно попадание;
- два попадания;
- три попадания;
А – не менее двух попаданий;
В – не более одного попадания;
С – не более двух попаданий.
Тогда: 
- (события несовместны);
;
Определение. Произведением событий А 1, А 2, …, А n называется такое событие 
, состоящее в том, что произошли все события А 1, А 2, …, А n одновременно.
Пример 1. А – выбранное число кратно 2. В – выбранное число кратно 3
А∙В – выбранное число кратно 6.
Пример 2. Произведено 3 выстрела по мишени. Введем такие события:
- попадание при первом выстреле;
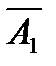- промах при первом выстреле;
- попадание при втором выстреле;
- промах при втором выстреле;
- попадание при третьем выстреле;
- промах при третьем выстреле;
А – три попадания;
В – ровно два попадания;
С – ни одного попадания;
D – хотя бы одно попадание.
Тогда согласно данным выше определениям:
1) 
; 2) 
;
3) 
; 4) 
.
Определение. Если полная группа событий состоит из двух событий, то любое из них называется противоположным к другому (обозначаются 
и 
). Следовательно, событие называется противоположным событию А, если оно состоит в том, что событие А не произошло.
Основные теоремы теории вероятностей. События А и В называются несовместными, если в результате одного опыта они не могут произойти одновременно, т. е. наступление одного из них исключает наступление другого.
Теорема 1. Вероятность суммы двух несовместных событий А и В равна сумме вероятностей событий А и В.
. (3.3)
Это правило можно обобщить на п событий. Если имеем п несовместных событий (А 1, А 2, …, А n), то вероятность суммы этих событий равна сумме вероятностей этих событий.
Следствие. Сумма вероятностей двух противоположных событий равна 1. 
(событие достоверное), 
, отсюда
. (3.4)
Два А и В события называются совместными, если появление обоих событий возможно в данном испытании.
Теорема 2. Вероятность суммы двух совместных событий А и В равна сумме вероятностей событий А и В минус вероятность их совместного появления.
. (3.5)
Следствие. Вероятность суммы трех совместных событий
.
Событие В называется зависимым от события А, если его появление зависит от того, произошло событие А или нет. Вероятность события В при условии, что А произошло, называется условной вероятностью события В при условии, что А произошло. Такая вероятность обозначается или 
или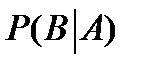 
.
Теорема 3. Вероятность произведения зависимых событий А и В равна произведению вероятности события А на условную вероятность события В , т.е. вычисленную при условии, что событие А произошло.
. (3.6)
Следствие 1. Теорема обобщается на любое конечное число событий:
События А и В называются независимыми, если вероятность одного из них не зависит от того, произошло ли второе событие. В этом случае условная вероятность события совпадает с безусловной вероятностью 
Теорема 4. Вероятность произведения независимых событий равна произведению вероятностей.
. (3.7)
Это выражение носит название критерия независимости случайных событий.
Пример. Производятся два независимых выстрела в одну и ту же мишень. Вероятности попадания: при первом выстреле - 0,6, при втором – 0,8. Найти вероятность попадания при двух выстрелах.
Решение. Примем: события 
и 
- попадание при 1-м и 2-м выстрелах соответственно. Попадание в мишень при двух выстрелах – это попадание при 1-м, либо при 2-м, либо при 1-м и 2-м выстрелах одновременно
.
События независимы, поэтому
.
Окончательно получаем
.
