Закон распределения Пуассона

Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Пусть число испытаний п достаточно велико , а вероятность появления события А в каждом испытании мало 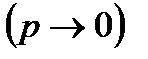, при этом произведение пр сохраняет постоянное значение. Обозначим .

Дискретная случайная величина Х имеет закон распределения Пуассона с параметром , если она принимает значения 0,1,2,…, ,… (бесконечное, но счетное множество значений) с вероятностями

 

                                                              (4.10)

 

где т -число появлений события в п независимых испытаниях,  (среднее число появлений события в п испытаниях).

Ряд распределения закона Пуассона имеет вид:

 

 

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого закона, т.е.

 

.

 

Замечание. При достаточно больших п (точнее, при ) и малых значениях р () и при условии, что произведение , закон распределения Пуассона является хорошим приближением биномиального закона. Так как при этом вероятность р события А в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Пример. Для продвижения своей продукции на рынок фирма раскладывает по почтовым ящикам рекламные листки. Прежний опыт работы показывает, что примерно в одном случае из 2 000 следует заказ. Найти вероятность того, что при размещении 10 000 рекламных листков поступит хотя бы один заказ, среднее число поступивших заказов и дисперсию числа поступивших заказов.

Решение. Здесь . Отсюда

.

 

Вероятность того, что поступит хотя бы один заказ, найдем через вероятность противоположного события, т.е.

.

 

Простейший поток событий.

Наряду с «предельным» случаем биномиального распределения закон Пуассона может возникнуть и в ряде других ситуаций. Рассмотрим их.

Если однотипные события происходят последовательно во времени, то они образуют поток событий.

Если в любой момент времени может произойти не более одного события (одно или ни одного), то поток называется ординарным.

Если вероятность того, что за время  произойдет  событий потока, не зависит от начала отсчета времени , то поток называется стационарным.

Если число событий, наступивших после данного произвольного момента времени  не зависит от того, сколько их произошло до этого момента, то поток называется потоком без последствий.

Определение. Ординарный, стационарный поток без последствийназывается простейшим потоком или пуассоновским потоком.

Обозначим  среднее число событий простейшего потока в единицу времени, оно называется плотностью потока.

Рассмотрим случайную величину , значения которой равны числу событий простейшего потока за время . Очевидно, что множество всех ее значений .

Вероятность того, что за время  произойдет ровно  событий потока находится по формуле  

 

.                                                                  (4.11)

Закон Пуассона имеет большое прикладное значение, так как ему подчиняются такие характеристики, как обрывность в прядении и ткачестве, число сбоев на автоматической линии, число отказов сложной системы в «нормальном режиме», число заявок на внеплановый ремонт технологического оборудования и т.д.

Пример. Обрывность в прядильном цехе составляет 100 обрывов на 1000 веретен в час. Найти вероятность того, что за смену (8 ч.) на одном веретене произойдет 4 обрыва.

Решение.  100 обрывов на 1000 веретен в час – это средняя обрывность,

т.е. математическое ожидание обрывности. Поэтому плотность числа обрывов на одном веретене в час составит 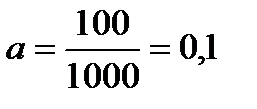 (обрывов в час).

Тогда в соответствии с формулой Пуассона, получим при :

 

.

 

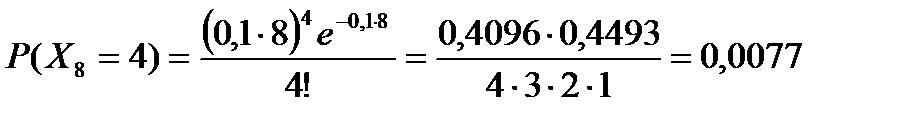Эта вероятность столь мала, что событие  практически невозможно. Если, тем не менее, такое событие произошло, то делают вывод, что указанное веретено требует наладки, так как при средней обрывности 100 обрывов на 1000 веретен в час на одном веретене за смену практически не может произойти 4 обрыва.

 

4.5.  Непрерывные случайные величины.

Рассмотрим случайные величины, значения которых занимают сплошь некоторый интервал, т.е. такие величины, множество которых не составляет числовой последовательности. Примерами таких величин могут быть масса тела, прочность, длина и т. п.

Определение. Случайная величина Х называется непрерывной, если множество ее допустимых значений занимает сплошь некоторый промежуток конечный или бесконечный.

Функцией распределения F (x) или интегральным законом распределения непрерывной случайной величины X называется вероятность выполнения неравенства X < х, т. е. вероятность того, что значения случайной величины Х попадают в интервал

                                                                        (5.1)

Для непрерывных случайных величин функция распределения F (x) непрерывна и кусочно дифференцируема на всей оси.

Определение функции распределения имеет наглядную геометрическую интерпретацию. Если рассматривать X как случайную точку на числовой оси, то F (x) есть вероятность того, что случайная точка попадет левее выбранной величины х (рис. 5.1).

Рис. 5.1. Геометрическая интерпретация функции распределения

 

Свойства функции распределения непосредственно вытекают из ее определения (ри с. 5.2):

1) F (x) - неотрицательная функция, значения которой заключены между 0 и 1, т.е.

0 £ F (x) £ 1;                                                                       (5.2)

2) F (-¥) = 0;                                                                              (5.3)

3) F (+¥) = 1;                                                                             (5.4)

4) F (x) - неубывающая функция своего аргумента, т.е. если x ₂ > х ₁, то F (x ₂) ³ F (x ₁);

5) P (a £ Х < b) = F (b) - F (a).                                               (5.5)                                                                                                          

Рис. 5.2. График функции распределения для непрерывной случайной величины

 

Основное свойство непрерывной величины. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю. Заметим, что в этом свойстве нет противоречия со здравым смыслом. Действительно, если мы говорим, что масса тела равна, например, 10 г, то подразумеваем, что она равна , где  - половина цены деления прибора, с помощью которого мы измеряли массу. Следовательно, мы получаем не отдельное значение, а интервал значений. Интервалу же значений соответствует, вообще говоря, ненулевая вероятность.

Замечание 1. Множество значений непрерывной случайной величины не являются последовательностью, закон ее распределения не может быть задан таблицей.

Замечание 2. Так как , то для непрерывных случайных величин нет разницы между строгими и нестрогими неравенствами:

 

. (5.6)

 

Если случайная величина не принимает значений на интервале , то она задается системой 

 

,      

 

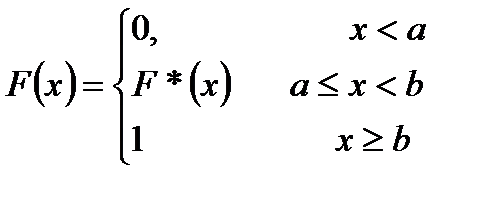где - часть функции F (x) на промежутке .

Если функция распределения непрерывна, то в любой точке предел этой функции слева равен пределу справа, в том числе и в точках , т.е. . Поэтому справедлива система

 

 

Пример. Случайная величина Х непрерывна и определена на  и имеет функцию распределения . Найти А и В.

Решение. На основании свойств функции распределения (равенства пределов справа и слева в точках ) имеем

.

 

Плотностью вероятности 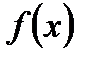непрерывной случайной величины Х называется производная от ее функции распределения, т. е.

 

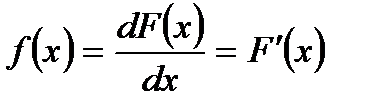.                                                                     (5.7)

 

Тем самым, функция распределения F (x) является первообразной для плотности и может быть задана через плотность по формуле

 

                                                                          (5.8)