Повторные независимые испытания. Формула Бернулли

На практике часто приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний при данном комплексе условий, в которых представляет интерес вероятность числа т наступлений некоторого события  в п испытаниях. Например, необходимо вычислить вероятность определенного числа попаданий при нескольких выстрелах в мишень, вероятность некоторого числа бракованных изделий в данной партии изделий и т. п.

 Если вероятность наступления события  в каждом испытании не изменяется в зависимости от исходов других, то такие испытания называются независимыми относительно события А. Если испытания проводятся в одном и том же комплексе условий, то вероятность  наступления события   в каждом испытании одна и та же. Описанная последовательность независимых испытаний получила название схемы Бернулли.

Теорема. Если производится п независимых испытаний, в каждом из которых вероятность  появления события А одна и та же и равна р, то вероятность того, что событие А появится в этих событиях m раз (безразлично в какой последовательности), выражается формулой Бернулли.

                                                                        (3.9)                                                                                                        

где q =1- p.                                                                                                      

При этом заметим, что наступление или ненаступление события  могут чередоваться в любом порядке.

Пример.   В урне 20 белых и 10 черных шаров. Вынули подряд 4 шара, причем каждый вынутый шар возвращают обратно перед извлечением следующего. Какова вероятность того, что из четырех вынутых шаров 2 белых?

Решение. Вероятность появления белого шара, которую можно считать постоянной во всех испытаниях р = Р (Бел) = . Вероятность не появления белого шара, т. е. вероятность появления черного шара q = P(Чер) = 1 - р = . Искомая вероятность может быть найдена по формуле Бернулли: .

4.4 Случайные величины

Под случайной величиной понимается переменная (величина), которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно заранее неизвестно). Названия случайных величин обычно обозначают заглавными буквами: X, Y, Z,…, а их возможные значения – прописными буквами: x, y, z ….

Рассмотрим примеры.

Проводятся выборы в представительные органы власти. Случайным событием является факт выбора (или не выбора) того или иного кандидата. При этом несомненный интерес представляет количество поданных за него голосов – случайная величина, количественно характеризующая результаты выборов.

Проводится социальное обследование, в котором изучается социальный портрет жителей данного района (города). Случайно выбранному жителю задаются вопросы о его социальной принадлежности, профессии, возрасте, семейном положении, обеспеченности жильем и т.п. Случайным событием является факт опроса того или иного жителя. Количественным же результатом опроса выступает вектор значений, каждый компонент которого есть количественная мера соответствующей характеристики опрашиваемого.

 Будем рассматривать случайные величины двух видов: дискретные и непрерывные.

Случайная величина называется дискретной, если множество ее допустимых значений составляет конечную или бесконечную числовую последовательность.

Примеры дискретных случайных величин:

1) - число выстрелов в цель до первого попадания. Теоретически это может быть бесконечная последовательность ;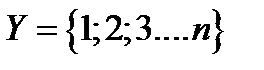

2) количество приборов, которые необходимо проверить до выявления первого неисправного;

3) количество уголовных дел, рассматриваемых данным судом за определенное время;

4) количество избирателей округа, которые примут участие в предстоящих выборах

5) Число родившихся детей в течение суток в С.-Петербурге и т. п.

Непрерывной называют такую случайную величину, возможные значения которой непрерывно заполняют некоторый промежуток числовой оси или всю ось.

Примеры: скорость автомобиля, проезжающего данный отрезок пути, составляет интервал ; время выхода из строя работающего компьютера, дальность полета артиллерийского снаряда и т. п.

Законом распределения вероятностей случайной величины (или просто законом распределения) называют всякое правило, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

Случайная величина полностью описана, если задан ее закон распределения.