Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) или графически.
Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены в порядке возрастания значения случайной величины  и соответствующие им вероятности
и соответствующие им вероятности 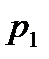 ,
,  ,…
,… 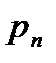 . Поскольку события
. Поскольку события 
 , значения, которые принимает случайная величина, являютсянезависимыми и единственно возможными, то они образуют полную группу событий, следовательно,
, значения, которые принимает случайная величина, являютсянезависимыми и единственно возможными, то они образуют полную группу событий, следовательно,
 . (4.1)
. (4.1)

| 
| 
| …. | 
|

| 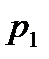
| 
| … | 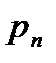
|
Такая таблица называется рядом распределения дискретной случайной величины.
Пример 1. Вероятности того, что студент сдаст семестровый экзамен по дисциплинам А и Б равны соответственно 0,7 и 0,9. Составить закон распределения числа сданных за семестр экзаменов.
Решение. Возможные значения случайной величины Х (числа сданных экзаменов) – 0, 1, 2.
Пусть событие  - событие, состоящее в том, что студент сдаст экзамен (
- событие, состоящее в том, что студент сдаст экзамен ( ). Тогда вероятности, что студент сдаст в сессию 0, 1, 2 экзамена будут:
). Тогда вероятности, что студент сдаст в сессию 0, 1, 2 экзамена будут:

Ряд распределения имеет вид:
 Контроль:
Контроль:  .
.
Пример 2. В партии из 6 деталей имеются 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения случайной величины Х – числа стандартных деталей среди отобранных.
Решение. Случайная величина Х имеет следующие возможные значения:  .
.
Найдем вероятности возможных значений Х, используя классическое определение вероятности (непосредственный подсчет событий):
 ,
,
где N - число деталей в партии, n - число стандартных деталей в партии, m - число отобранных деталей, k -число стандартных деталей среди отобранных. Находим
 ,
,
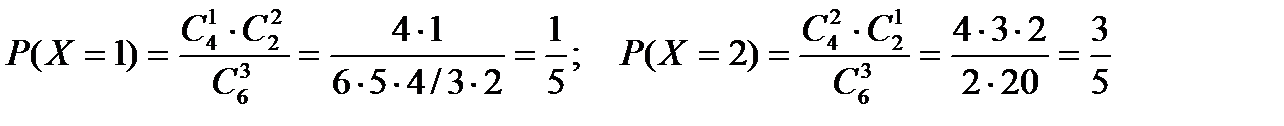 ;
; 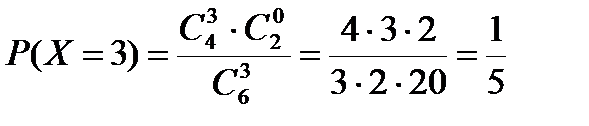 .
.
Закон распределения:
 Контроль:
Контроль:  .
.
Числовые характеристики дискретных случайных величин. При решении многих задач теории вероятностей вовсе не обязательно знать закон распределения данной случайной величины, полностью ее описывающий. Достаточно знать так называемые числовые характеристики ее распределения, т.е. числовые параметры, характеризующие наиболее важные черты ее закона распределения.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
 .(4.2)
.(4.2)
Математическое ожидание можно рассматривать как среднее вероятностное значение случайной величины, учитывая, что каждое возможное значение  входит со своим «весом», которым и является вероятность
входит со своим «весом», которым и является вероятность  . Так, если все значения
. Так, если все значения  равновероятны, то математическое ожидание будет равно среднему арифметическому всех возможных значений:
равновероятны, то математическое ожидание будет равно среднему арифметическому всех возможных значений:
 . (4.3)
. (4.3)
Пример. В магазин ежедневно поступает не более пяти компьютеров, т. е. от нуля до пяти. Известны вероятности поступления соответствующего числа компьютеров:

Найти математическое ожидание числа поступлений компьютеров.
Решение. Закон распределения вероятностей

 .
.






