Пусть дано n неизвестных x 1, x 2, xi, …, xn. Система m линейных уравнений с n неизвестными xi,  , имеет вид
, имеет вид
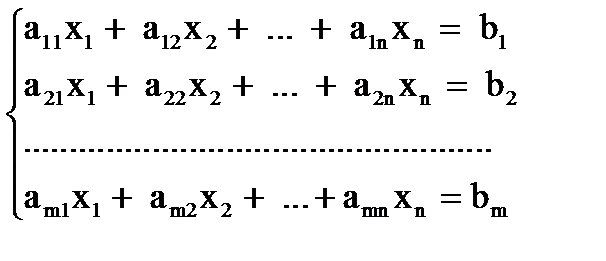 (2.1)
(2.1)
здесь аij коэффициенты при неизвестных, причем i – номер уравнения, а j – номер неизвестного. Величины b i - свободные члены. В матричной форме систему можно записать так
A∙X = B, (2.2)
где 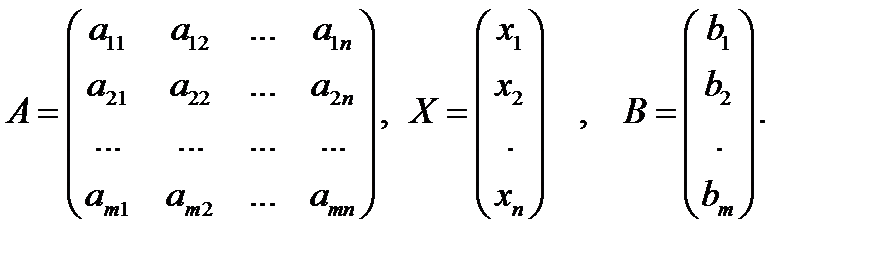
Матрица А называется матрицей коэффициентов, матрица В – матрица столбец свободных членов, матрица Х – матрица столбец неизвестных. Если к матрице коэффициентов системы приписать матрицу столбец свободных членов, то получится расширенная матрица системы уравнений А расш или (A | B)
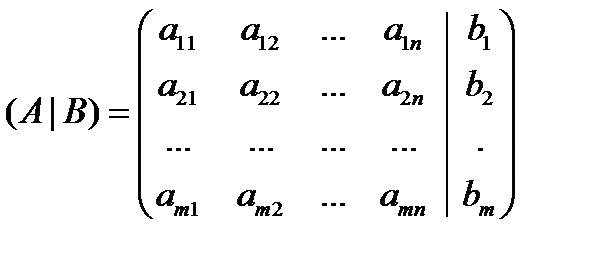 (2.3)
(2.3)
Система трех уравнений с тремя неизвестными имеет вид
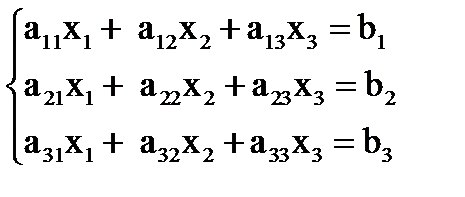 , где
, где 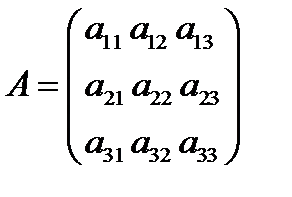 ,
, 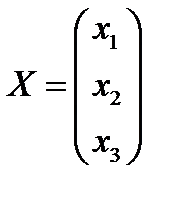 ,
,  ,
,
(A | B) = 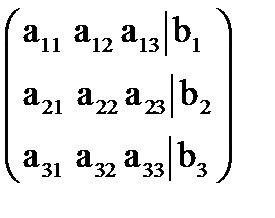 .
.
Если все свободные члены bi равны нулю, то система называется однородной, в противном случае система неоднородна. Линейные системы, полученные одна из другой путем элементарных преобразований (перестановкой двух уравнений, умножением одного из них на число, не равное нулю, почленным сложением двух уравнения) называются эквивалентными (или равносильными). Все эквивалентные системы имеют одинаковые решения.
Решение системы линейных алгебраических уравнений с помощью формул Крамера.
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:
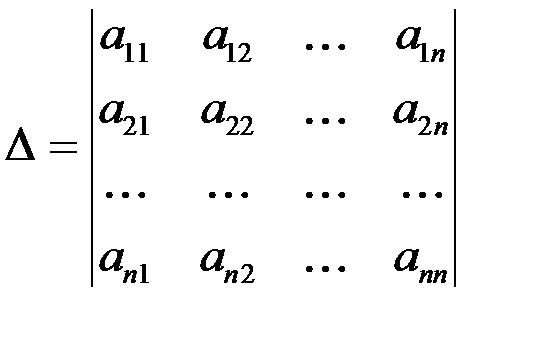 .(2.5)
.(2.5)
Если  ¹0, то система (2.4) имеет решение, и при том единственное. Если
¹0, то система (2.4) имеет решение, и при том единственное. Если  = 0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
= 0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
В дальнейшем мы будем предполагать, что  ¹0.
¹0.
Решение с помощью формул Крамера.
Если определитель системы  ¹0, то, согласно формулам Крамера, решение системы (2.4) можно представить в виде
¹0, то, согласно формулам Крамера, решение системы (2.4) можно представить в виде
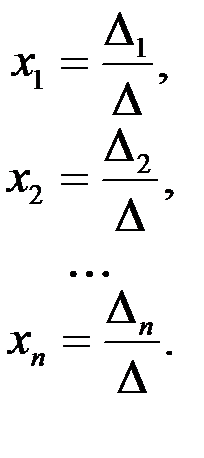 (2.6)
(2.6)
Где 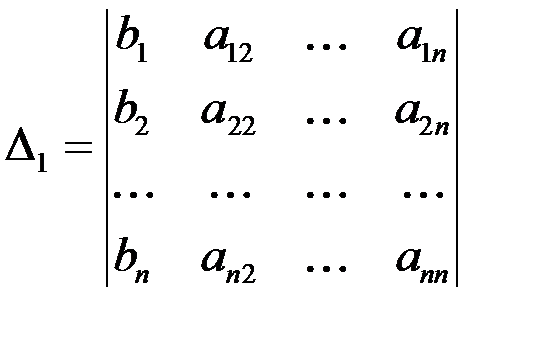 ,
, 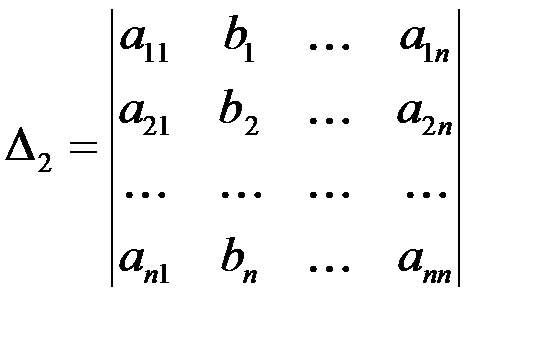 ,…,
,…, 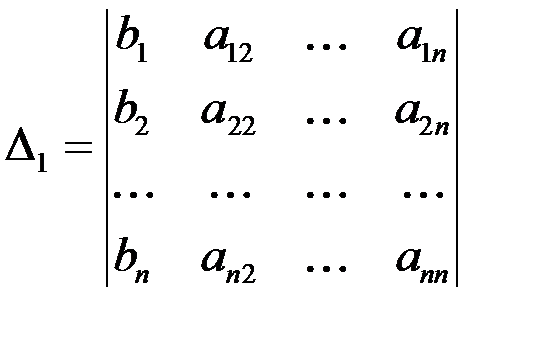 .
.
Определитель 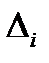 (i =1, 2,…, n) отличается от определителя системы
(i =1, 2,…, n) отличается от определителя системы  тем, что
тем, что  столбец в определителе
столбец в определителе  заменен столбцом из свободных членов, т.е. столбец
заменен столбцом из свободных членов, т.е. столбец
 заменен на столбец
заменен на столбец 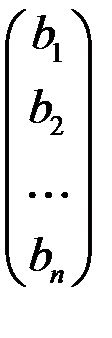 .
.
Пример. Дана расширенная матрица системы 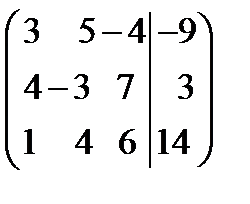 . Решить систему методом Крамера.
. Решить систему методом Крамера.
Решение. Запишем систему в стандартной форме
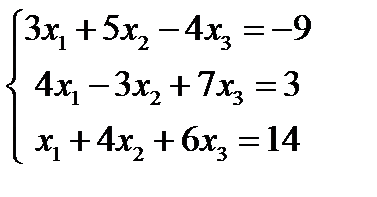 .
.
Определитель данной системы
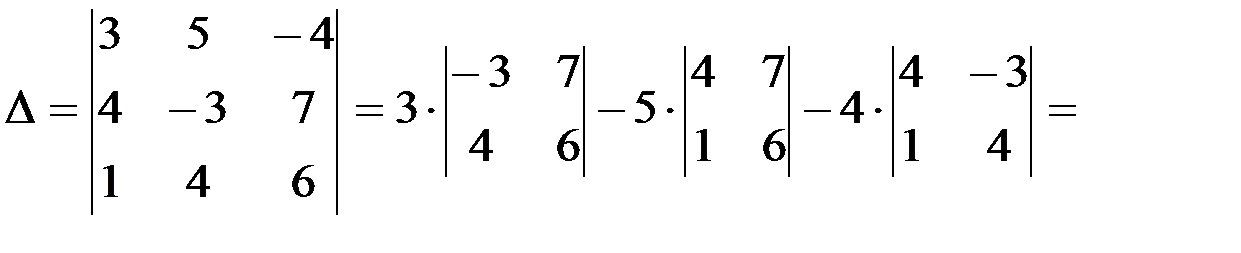
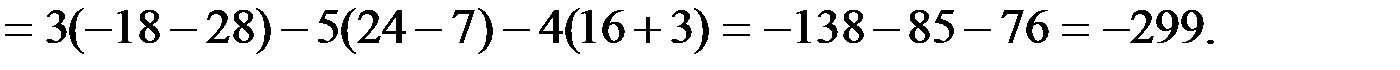
Вычислим определители 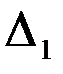 ,
, 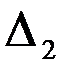 и
и 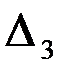 :
:
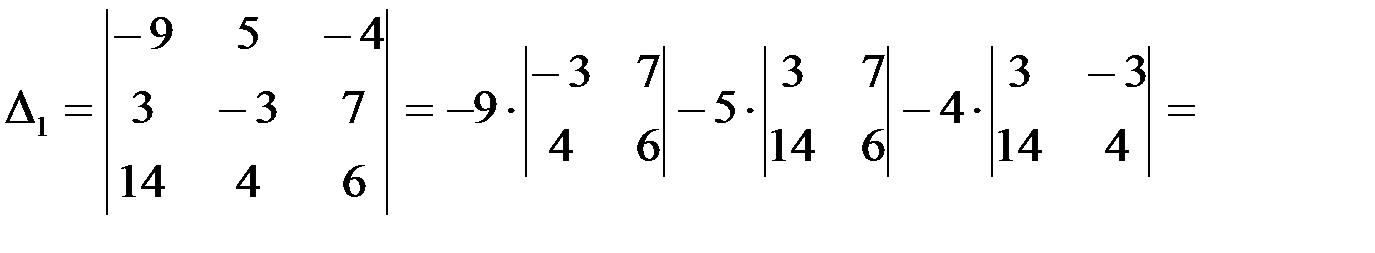
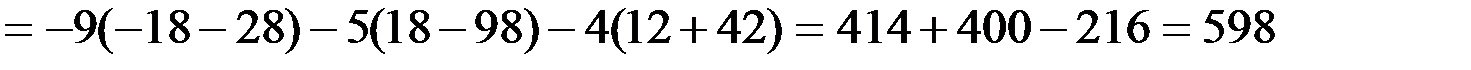 .
.
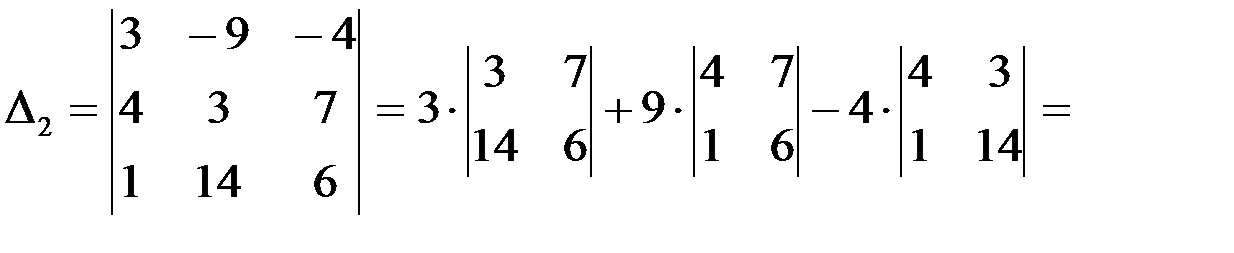
 .
.
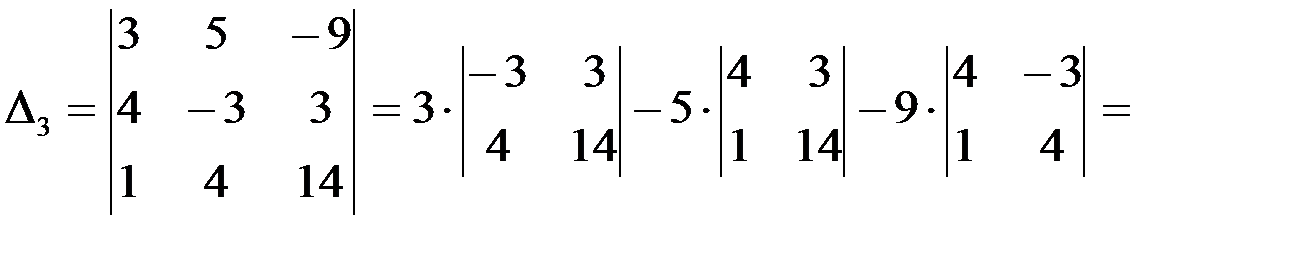
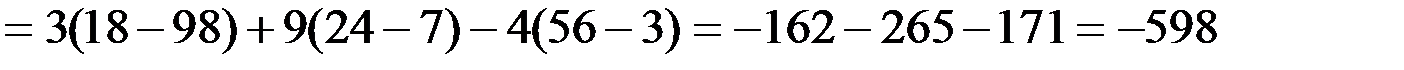 .
.
Решение системы: 
Для того чтобы убедиться в правильности решения, подставим эти значения 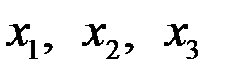 в исходную систему
в исходную систему
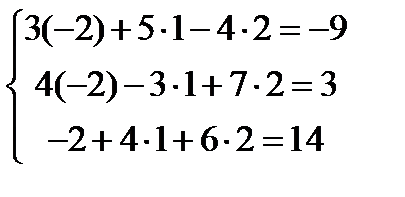 .
.
Решение методом Гаусса. Пусть есть система (2.4)с определителем  ¹0. Напишем расширенную матрицу, в которой содержится вся информация о сисеме
¹0. Напишем расширенную матрицу, в которой содержится вся информация о сисеме
(А | B)= 
Метод Гаусса состоит в том, что система (2.4) с помощью ряда элементарных преобразований сводится к новой системе, расширенная матрица которой имеет
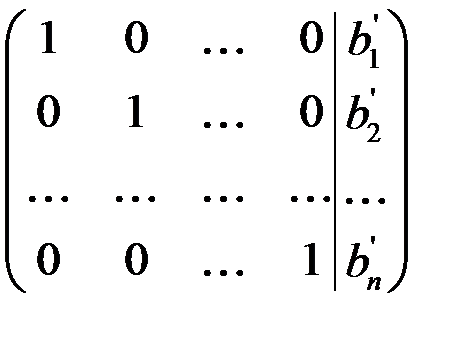
Т.е. в результате преобразований все коэффициенты матрицы 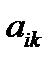 становятся равными нулю, кроме диагональных элементов, которые становятся равными единице:
становятся равными нулю, кроме диагональных элементов, которые становятся равными единице:  при
при 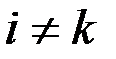 и
и 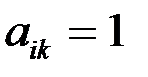 при
при  .
.
Столбец свободных членов 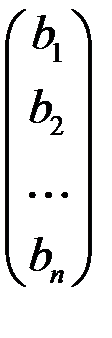 превращается в столбец
превращается в столбец 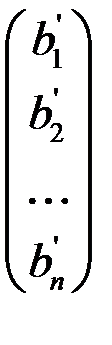 где и стоят решения
где и стоят решения
системы 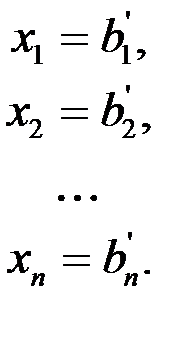
Таким образом, решение системы сводится к совершению элементарных преобразований. К элементарным преобразованиям системы относятся следующие:
1) перемена местами уравнений (т.е. перемена местами строк расширенной матрицы);
2) умножение или деление любого уравнения системы на число, отличное от 0 (т.е. умножение или деление строки расширенной матрицы на число, отличное от 0);
3) изменение любого уравнения системы путем прибавления к нему другого уравнения системы, умноженного на число, отличное от 0 (т.е. изменение строки расширенной матрицы путем прибавления к ней другой строки, умноженной на число, отличное от 0).
Пример. Найти методом Гаусса решение системы. 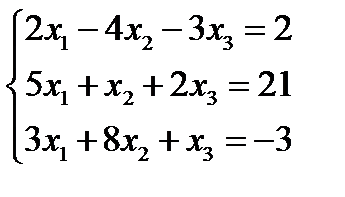 .
.
Решение. Определитель системы  . Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
. Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
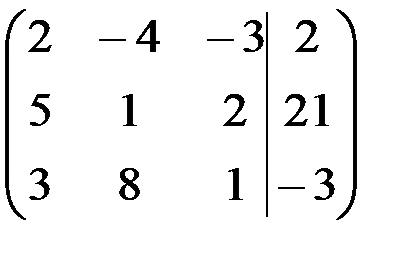 .
.
Далее мы будем приводить нашу матрицу к диагональному виду и выписывать ее вид после каждого шага преобразований.
1-й шаг. Разделим 1-ю строку матрицы на 2.
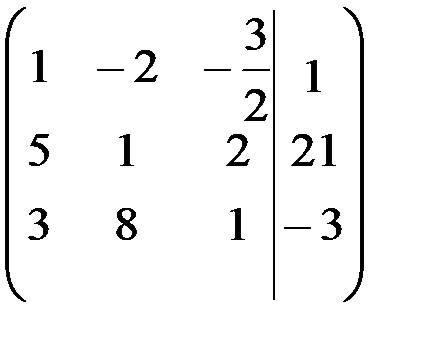 .
.
2-й шаг. 1-ю строку оставляем без изменения. Вместо 2-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-5), складываем ее со 2-й строкой, тогда новые числа, стоящие во 2-й строке расширенной матрицы, будут следующие:
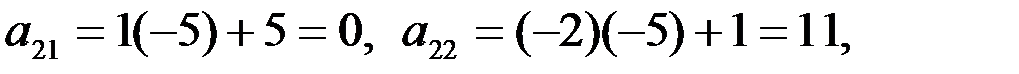
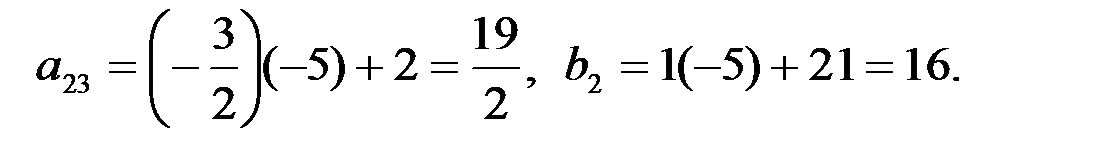
Вместо 3-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-3) и складываем ее с 3-й строкой, тогда

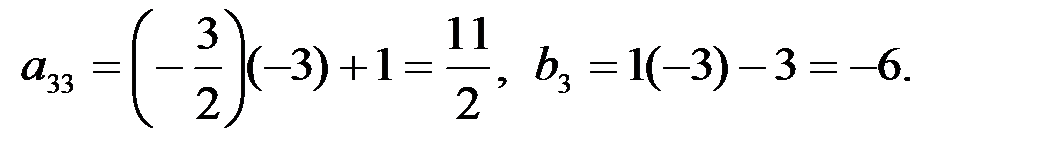
Расширенная матрица примет вид
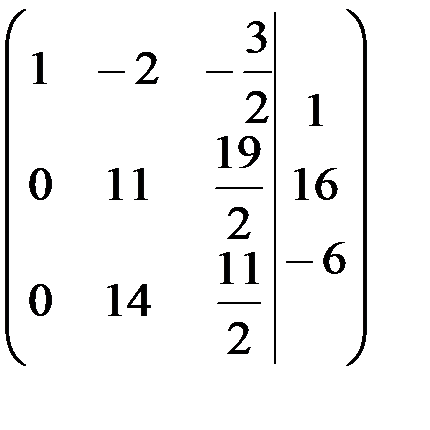 .
.
В результате первых 2-х шагов 1-й столбец 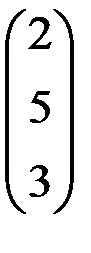 преобразовался в
преобразовался в 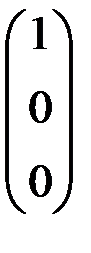 .
.
3-й шаг. Делим вторую строку на 11.
 .
.
4-й шаг. 2-ю строку оставляем без изменения. Вместо 1-й строки записываем следующую ее комбинацию со 2-й: 2-ю строку умножаем на 2 и складываем ее с 1-й строкой, тогда
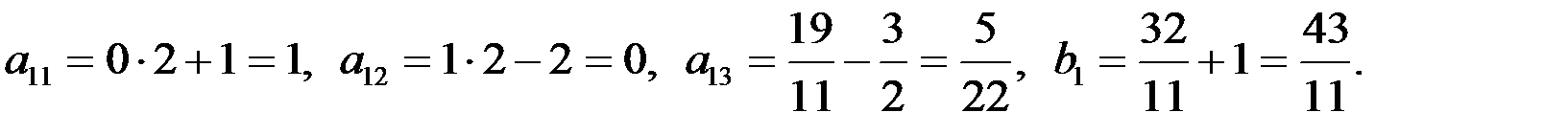
Вместо 3-й строки записываем ее комбинацию со 2-й: 2-ю строку умножаем на (-14) и складываем ее с 3-й строкой, тогда
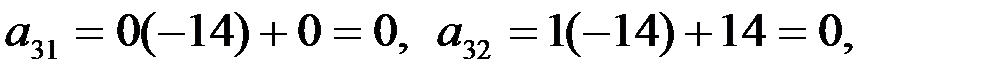
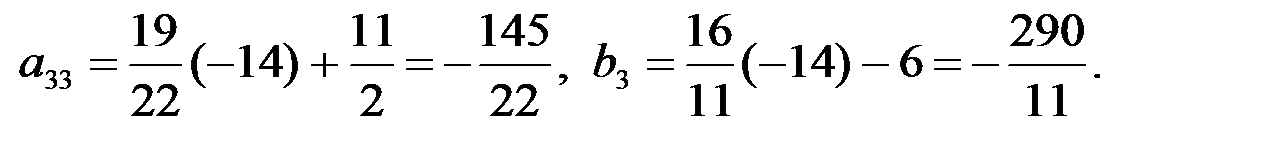
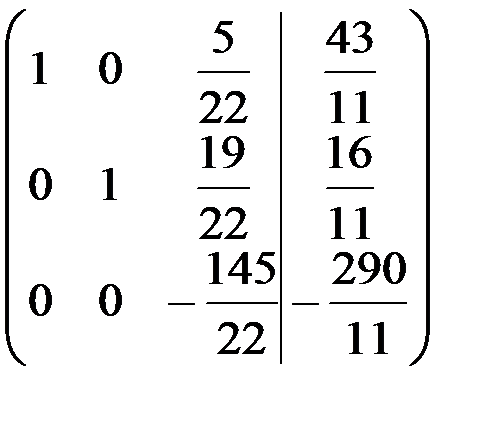 .
.
В результате 3-го и 4-го шагов 1-й столбец матрицы не изменился, а 2-й превратился в  .
.
5-й шаг. Делим 3-ю строку на 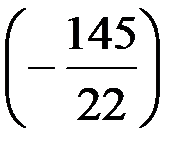
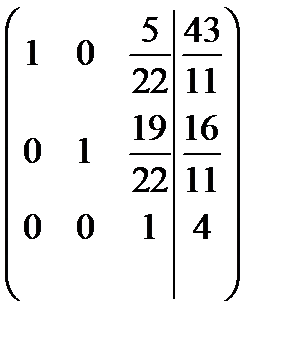 .
.
6-й шаг. 3-ю строку оставляем без изменения. Вместо 1-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на 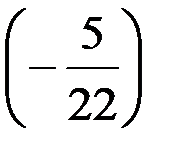 и складываем ее с 1-й строкой, тогда
и складываем ее с 1-й строкой, тогда

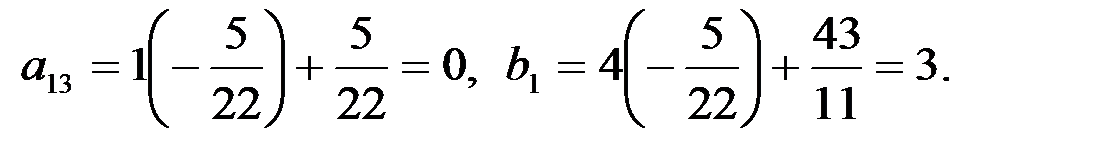
Вместо 2-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на 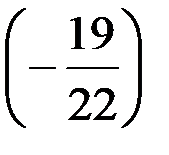 и складываем ее со 2-й строкой, тогда
и складываем ее со 2-й строкой, тогда
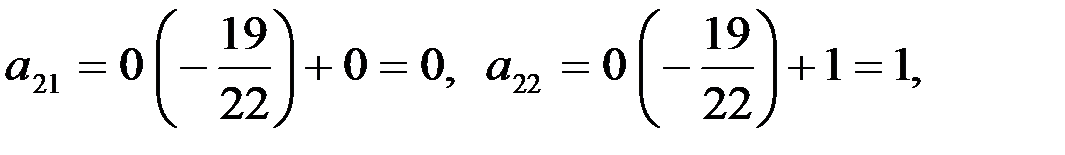
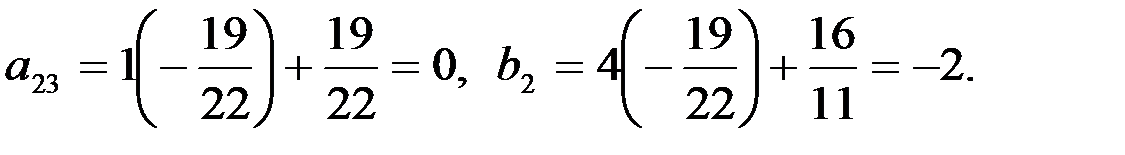
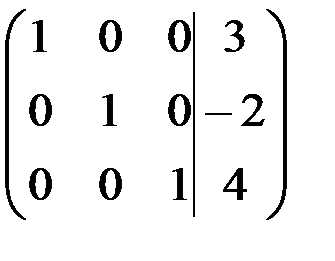 .
.
В результате 5-го и 6-го шагов 3-й столбец принял вид 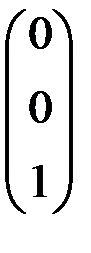 .Таким образом, решение системы следующее:
.Таким образом, решение системы следующее:  Проверка
Проверка

Решение методом исключений. Метод исключений является модификацией метода Гаусса и удобен для небольших систем.
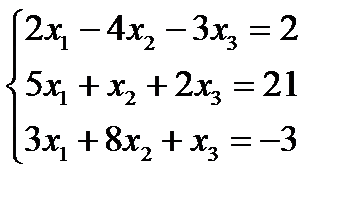 .
.
Умножим первое уравнение на коэффициент при х 1 из второго уравнения, т.е. на 5, а второе на коэффициент при х 1 из второго уравнения, т.е. на 2 и вычтем друг из друга. Потом умножим первое на коэффициент при х 1 из второго уравнения, т.е. на 3, а третье на 5 и снова вычтем
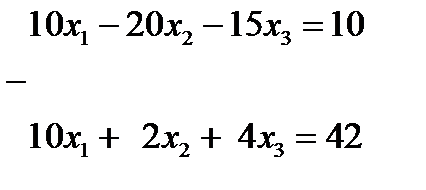

_______________________________ ___________________
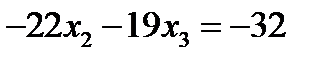
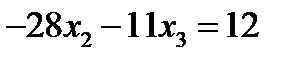
Поменяем в первом уравнении знаки и запишем подсистему
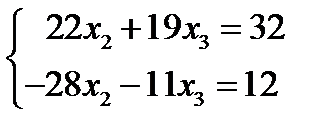
Умножим первое уравнение на 28, второе на 22 и сложим. Слагаемые с х 2 сократятся и мы получим уравнение для х 3
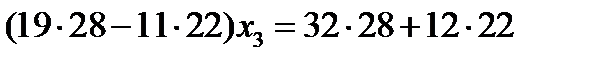
х 3 = 4, подставляя х 3 в первое уравнение подсистемы получим х 2
 , х 2 = -2,
, х 2 = -2,
Подставляя х 2 и х 3 в первое уравнение системы найдем х 1
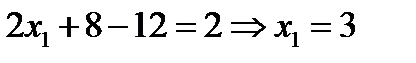
Объем вычислений при этом методе существенно меньше.
Векторная алгебра.
Вектором называется направленный отрезок прямой. Из определения следует, что вектор имеет три характеристики:
прямую на которой он лежит,
направление по прямой и длину.
Первые две характеристики объединяются одним понятием – направление. Обозначаются вектора по точкам начала и конца АВ или 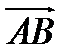 жирным шрифтом или знаком вектора сверху.
жирным шрифтом или знаком вектора сверху.
Различают три вида векторов:
свободные вектора, которые не меняются при параллельном переносе,
полусвободные вектора, которые можно переносить только по прямой на которой они лежат (например, вектора сил в механике),
радиус вектора, начало которых всегда находится в начале координат.
Мы будем рассматривать только свободные вектора. Свободные вектора называют равными, если они лежат на одной или параллельных прямых, направлены в одну сторону и имеют одинаковую длину (рис 3.1), т. е. параллельный перенос вектора не меняет. Свободные вектора обозначают одной буквой  или а. Длину вектора обозначают при помощи модульных скобок
или а. Длину вектора обозначают при помощи модульных скобок  = а или нежирным щрифом.
= а или нежирным щрифом.
Вектора складывают по правилу параллелограмма: совмещают концы векторов, строят на векторах как на сторонах параллелограмм; суммой векторов называют вектор диагонали исходящий их общего начала a + b = c (рис.3.2). Вектора можно складывать и по правилу треугольника (рис. 3.3). Правило треугольника можно применить к сумме любого числа векторов (рис 3.4)
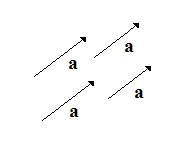
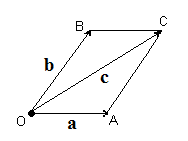
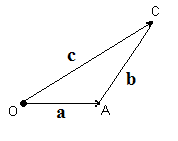
| Рис. 3.2. Рис. 3.3. Сложение векторов |
| Рис. 3.1 |
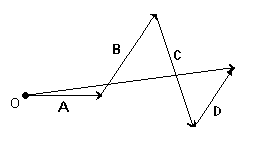
Умножение вектора на число λ идет по следующему правилу: при умножении на положительное число направление вектора сохраняется, при умножении на отрицательное – меняется на противоположное, а длина определяется по правилу (рис 3.5).
çλ а ç = 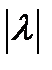 а (3.1)
а (3.1)
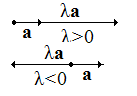
| Рис. 3.4 Сложение нескольких векторов |
| Рис. 3.5. Умножение вектора на число |
По определению a - b = a + (-1) b.
Проекцией вектора на ось ОХ называется число равное разности координат проекций конца и начала вектора
pr х AB = x 2 – x 1= ç AB ç cos (α), (3.2)
где α - угол между вектором и осью (рис. 3.6). Вектор А 1 В 1 называется составляющим вектором по оси ОХ. Аналогично можно ввести проекцию вектора АВ на оси OY и OZ:
pr у AB = y 2 – y 1= ç AB ç cos (β) (3.3а)
prZAB = z 2 – z 1= ç AB ç cos (γ), (3.3б)
где β и γ углы между вектором АВ и осями OY и OZ. Вектора А 2 В 2 и А 3 В 3 называются составляющими векторами по осям OY и OZ соответственно.
Косинусы углов cos (α), cos (β) и cos (γ) называют направляющими косинусами
cos 2(α)+ cos 2(β)+ cos 2(γ) = 1. (3.4)
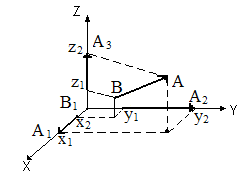
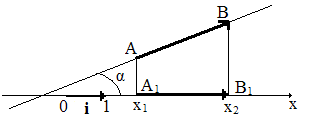
| Рис. 3.7.Разложение вектора АВ на сумму векторов, параллельных осямкоординат. |
| Рис. 3.6. Проекция вектора на ось ОХ |
Если ввести i, j и k - единичные вектора осей ОХ, OY и OZ (их называют ортами), то вектора
A1B 1 = i (x 2 – x 1), A 2 B 2 = j (y 2 – y 1) и A 3 B 3 = k (z 2 – z 1). (3.5)
По правилу сложения векторов (рис. 3.7):
AB = A 1 B 1 + A 2 B 2 + A 3 B 3 = i (x 2 – x 1) + j (y 2 – y 1) + k (z 2 – z 1) ≡
≡{(x 2 – x 1), (y 2 – y 1), (z 2 – z 1)}.
Равенство AB = i (x 2 – x 1) + j (y 2 – y 1) + k (z 2 – z 1) называется «запись вектора через составляющие вектора. Равенство
AB = {(x 2 – x 1), (y 2 – y 1), (z 2 – z 1)} (3.6)
называется «запись вектора в форме проекций». Числа (x 2 – x 1), (y 2 – y 1) и(z 2 – z 1) называются также координатами вектора
Операции с векторами a, b заданными в форме проекций
a = { x 1, y 1, z 1)}и b = { x 2, y 2, z 2} идут по следующим правилам:
a + b ={ (x 1+ x 2), (y 1 + y 2), (z 1 + z 2)}; (3.7)
λ a = {λ x 1, λ y 1, λ z 1}. (3.8)
Скалярным произведением векторов a = { x 1, y 1, z 1)}; b = { x 2, y 2, z 2} называют число равное произведению длин векторов на косинус угла между ними
а × b = (a,b) = ç a ç· ç b çcos(Ð a, b) = x 1 x 2 + y 1 y 2 + z 1 z 2. (3.9)
Замечание: скалярное произведение обозначается знаком  .
.
Скалярное произведение перестановочно: а × b = b × а. Если вектора перпендикулярны, то скалярное произведение равно нулю. Скалярное произведение векторов используют для определения длины вектора
а × a = x 1 x 1+ y 1 y 1 + z 1 z 1 = x 12+ y 12 + z 12 Þç a ç= 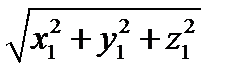 (3.10)
(3.10)
Пример. Найти угол φ между векторами 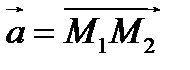 и
и 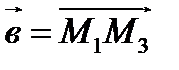 , если
, если
М 1(1, -2, -3), М 2(-3, 1, 1), М 3(3, 2, 2).
Решение. Для нахождения cosφ используем формулу 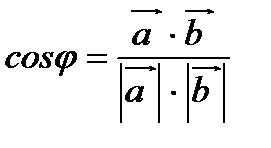 где
где 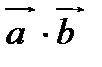 - скалярное произведение векторов
- скалярное произведение векторов 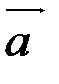 и
и 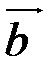 . Определим проекции (координаты) векторов
. Определим проекции (координаты) векторов 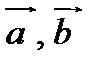 и cosφ. Если из координат точки М2 вычесть координаты точки М1, то получим вектор
и cosφ. Если из координат точки М2 вычесть координаты точки М1, то получим вектор 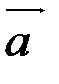 . Вектор
. Вектор 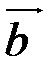 получим, если из координат точки М3 вычтем координаты точки М1.
получим, если из координат точки М3 вычтем координаты точки М1.
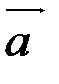 = (-3-1, 1+2, 1+3) =(-4, 3, 4),
= (-3-1, 1+2, 1+3) =(-4, 3, 4), 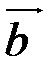 = (3-1, 2+2, 2+3) = (2, 4, 5),
= (3-1, 2+2, 2+3) = (2, 4, 5),
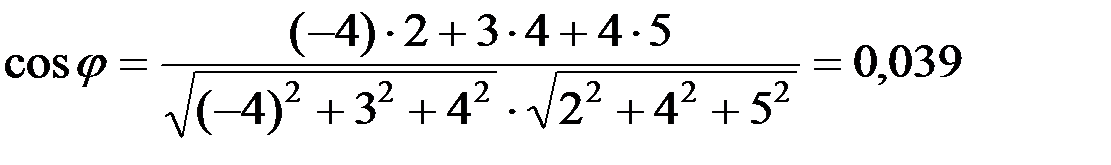 . → φ = 87045'54".
. → φ = 87045'54".
Векторным произведен ием векторов a и b называют такой вектор
c = a ´ b, который:
1. лежит на прямой перпендикулярной плоскости векторов a и b,
2. имеет длину численно равную произведению длин векторов на синус угла между ними (угол отсчитывается по наименьшему углу от первого вектора ка второму)
ç c ç = ç a ç· ç b ç sin (Ð a, b) = ç a ç· ç b ç sin (φ), (3.11)
3. направление вектора c определяется по правилу буравчика: если вращать рукоять буравчика от первого вектора ко второму по наименьшему углу, то поступательное движение буравчика показывает направление вектора c (рис. 3.8).
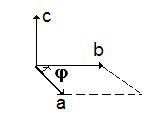
Рис. 3.8. Векторное произведение векторов
Замечание: векторное произведение обозначается знаком 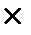 .
.
Из определения следует, что векторное произведение единичных векторов осей координат - ортов i, j, k равно
k = i ´ j, i = j ´ k, j = k ´ i. (3.12)
Векторное произведение не перестановочно: a ´ b = - b ´ a. Для коллинеарных векторов (лежащих на одной прямой) векторное произведение равно нулю a ´ b = 0, (a çç b). Для векторов заданных в форме проекций
с = a ´ b =  = i (y 1 z 2 – y 2 z 1) - j (x 1 z 2 – z 1 x 2) + k (x 1 y 2 – x 2 y 1). (3.13)
= i (y 1 z 2 – y 2 z 1) - j (x 1 z 2 – z 1 x 2) + k (x 1 y 2 – x 2 y 1). (3.13)
Длина вектора векторного произведение численно равна площади параллелограмма, построенного на векторах, как на сторонах:
S = ç a çç b ç sin (φ).
Смешанным произведением векторов a, b и c называется векторно-скалярное произведение
a ´ b × c = a × b ´ c º abc = 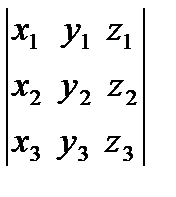 , (3.14)
, (3.14)
т. е. два вектора (первый – второй или второй – третий) перемножаются векторно, а третий вектор умножают на результат векторного произведения скалярно. В записи смешанного произведения знаки произведений обычно опускают. Смешанное произведение равно нулю, если векторы компланарны (лежат в одной плоскости). Смешанное произведение используют для вычисления объема параллелепипеда и пирамиды, построенной на векторах a, b, c.
V пар = ê abc ê; V пир =  ê abc ê. (3.15)
ê abc ê. (3.15)
Пример. Даны координаты вершин пирамиды А 1(1, -2, -3), А 2(-3, 1, 1), А 3(4, 3, -1), А 4(3, 2, 2). Найти площадь грани А 1 А 2 А 3 и объем пирамиды.
Решение. Площадь треугольника А 1 А 2 А 3 найдем, используя геометрический смысл векторного произведения векторов
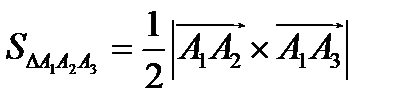 ,
,
где  - векторное произведение векторов.
- векторное произведение векторов.
Вначале находим 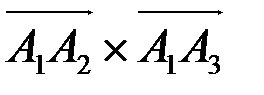
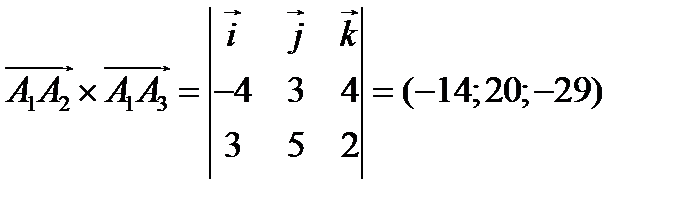 ,
,
а затем
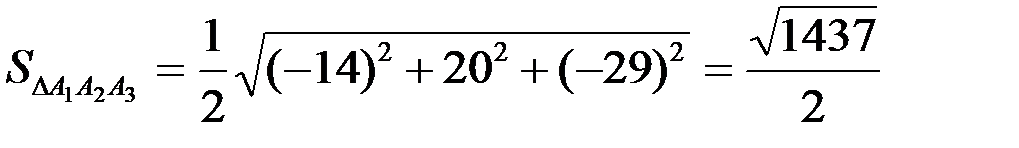 ед2.
ед2.
Объем пирамиды найдем, используя геометрический смысл смешанного произведения векторов
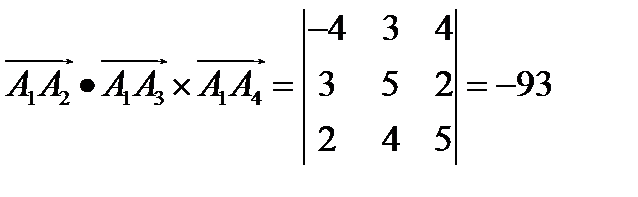 ,
,
следовательно,  ед3.
ед3.






