САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И ДИЗАЙНА»
Кафедра математики
Г. П. Мещерякова
Математика
Конспект лекций
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Санкт-Петербург
2018
УДК 51(075.8)
ББК 22.1я73
М 56
Р е ц е н з е н т ы:
Мещерякова, Г. П.
М 56 Математика. Конспект лекций: учеб. пособие / Г. П. Мещерякова,
ISBN 978-5-7937-1228-6
Конспект лекций по математике для направлений …..Лекции посвящены рассмотрению необходимых теоретических сведений по следующим разделам курса математики: линейная и векторная алгебры, введение в математический анализ и теория пределов, основы дифференциального и интегрального исчисления, теория вероятности и элементы математической статистики. Даны решения типовых задач.
УДК 51(075.8)
ББК 22.1я73
ISBN 978-5-7937-1228-6
© ФГБОУ ВО «СПбГУПТД», 2018
© Мещерякова Г. П., 2018
Оглавление
| Введение | 4 |
| 1. Линейная алгебра | 4 |
| 1.1. Матрицы. Правила действия с матрицами. | 4 |
| 1.2 Системы линейных алгебраических уравнений | 8 |
| 1.3.Векторная алгебра | 15 |
| 2Аналитическая геометрия на плоскости и в пространстве | 20 |
| 2.1. Геометрия на плоскости | 20 |
| Системы координат на плоскости | 20 |
| Прямая линия на плоскости | 23 |
| Кривые второго порядка | 27 |
| 2.2. Геометрия в пространстве | 32 |
| Системы координат в пространстве | 32 |
| Плоскость и прямая в пространстве | 34 |
| 3. Математический анализ | 38 |
| 3.1. Введение в анализ | 38 |
| Функциии. Основные определения | 38 |
| Предел функции | 41 |
| Правила вычисления пределов | 44 |
| Замечательные пределы | 46 |
| Непрерывность функции. Односторонние пределы | 49 |
| 3.2. Производная функции и дифференциал | 51 |
| Определение производной и правила дифференцирования | 51 |
| Связь между непрерывностью и дифференцируемостью функции | 58 |
| Теоремы о дифференцируемых функциях | 61 |
| Приложение производной к исследованию функций | 65 |
| 3.3. Функции многих переменных | 73 |
| Функции двух переменных | 73 |
| Экстремум функции двух переменных | 81 |
| 3.4. Неопределенный интеграл | 87 |
| Определение первообразной и определение неопределенного интеграла | 87 |
| Основные методы интегрирования | 89 |
| 3.5. Определенный интеграл | 98 |
| Определение определенного интеграла | 98 |
| Выычисление определенного интеграла | 103 |
| Несобственные интегралы | 107 |
| Приложения определенного интеграла | 109 |
| 3.6. Дифференциальные уравнения | 114 |
| Основные понятия теории дифференциальных уравнений | 114 |
| Дифференциальные уравнения первого порядка | 118 |
| Дифференциальные уравнения второго порядка | 123 |
| 3.7. Последовательности и ряды | 129 |
| 7.1. Числовые ряды | 129 |
| Признаки сходимости числовых рядов с положительными членами | 134 |
| Знакочередующиеся ряды | 139 |
| 7.2. Степенные ряды | 140 |
| 4. Теория вероятностей | 145 |
| 4.1. Элементы комбинаторики | 145 |
| 4.2. Случайные события | 149 |
| 4.3. Понятие вероятности | 150 |
| Алгебра событий. Основные теоремы теории вероятностей | 152 |
| Повторные независимые испытания. Формула Бернулли | 156 |
| 4.4. Случайные величины | 157 |
| Дискретные случайные величины | 158 |
| Основной закон распределения дискретной случайной величины | 163 |
| Простейший поток событий | 165 |
| 4.5. Непрерывные случайные величины | 167 |
| 5. Элементы математической статистики | 178 |
| 5.1.Основы выборочного метода. Методы отбора. Понятие репрезентативности выборки. Генеральное и выборочное среднее, генеральная и выборочная дисперсия | 178 |
| 5.2.Оценка параметров генеральной совокупности по данным выборки. | 182 |
| Заключение | 189 |
| Библиографический список | 189 |
| Приложение А | 191 |
Введение
Данный курс лекций включает все основные разделы курса математики, которые входят в программу для студентов, изучающих математику два семестра. Особый акцент делается на теорию вероятностей и статистику, так как вводимые в этих разделах математики понятия используются в последующих прикладных курсах. Приводится большое количество примеров и задач. Курс может быть рекомендован студентам всех форм обучения как электронный конспект лекций.
Линейная алгебра
Матрицы. Правила действия с матрицами
Матрицей А называется прямоугольная таблица чисел. Если матрица состоит из m строк и n столбцов, то говорят, что размерность матрицы есть m на n (m 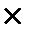 n). Количество элементов в такой матрице равно произведению m ∙ n. Обозначение матрицы
n). Количество элементов в такой матрице равно произведению m ∙ n. Обозначение матрицы
 (1.1)
(1.1)
Числа aij, составляющие матрицу, называются ее элементами. Первый индекс i указывает номер строки, второй j - номер столбца.
Матрица называется прямоугольной, если m ≠ n, Если m = n, то матрица называется квадратной и число n - порядком матрицы. Матрица, содержащая один столбец, называется матрица-столбец. Матрица, состоящая из одной строки - матрица-строка. У таких матриц элементы могут иметь только один номер.
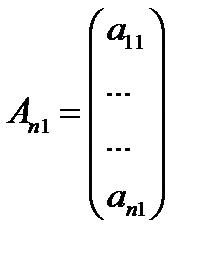 ;
;  (1.2)
(1.2)
Матрица, все элементы которой равны нулю, называется нулевой матрицей. Для квадратной матрицы порядка n элементы с одинаковыми индексами a 11, a 22,..., ann образуют главную диагональ. Элементы a 1 n, a 2 n -1,..., an 1 образуют побочную диагональ. Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали, равны нулю: aij = 0 при i ≠ j. Диагональная матрица обозначается так
 . (1.3)
. (1.3)
Диагональная матрица, у которой все диагональные элементы равны, единице называется единичной и обозначается I или E
 (1.4)
(1.4)
Квадратная матрица называется треугольной, если все элементы, стоящие ниже (или выше) главной диагонали, равны нулю:
 ,
,  . (1.5)
. (1.5)
Каждой квадратной матрице ставится в соответствие число, называемое детерминантом или определителем, который обозначается символами detA или D(A).
Для матрицы  определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали
определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали
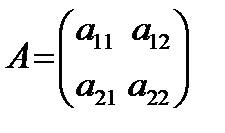 det(A) =
det(A) = 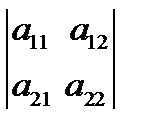 = a 11 a 22 – a 12 a 21. (1.6)
= a 11 a 22 – a 12 a 21. (1.6)
Для матрицы  определитель находится по формуле
определитель находится по формуле

(1.7)
det (A) =  = a11 a22 a33 + a12 a23 a31 + a13 a21a32 - a13a22 a31 –
= a11 a22 a33 + a12 a23 a31 + a13 a21a32 - a13a22 a31 –
- a12 a21 a33 - a11a23 a32.
Пример. Вычислить определитель матрицы 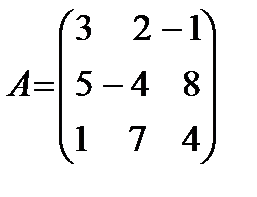 .
.
Решение.

Определитель единичной матрицы равен единице det I = 1.
Минором Mik называется определитель меньшего порядка (размера), полученный при вычеркивании i -той строки и k -того столбца. Алгебраическим дополнением Aik называется минор, знак которого определяется по правилу Aik = (-1) i + k Mik.
Определитель можно представить в виде суммы произведений элементов любой строки или столбца на их алгебраические дополнения, например для матрицы 3×3
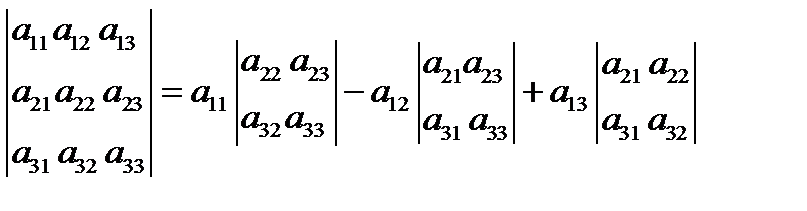 (1.8)
(1.8)
Квадратная матрица называется невырожденной (неособенной), если det A ¹0, и вырожденной (особенной), если det A =0. Определитель треугольной матрицы равен произведению диагональных элементов:
 . (1.9)
. (1.9)
Действия над матрицами. Равенство матриц. Две матрицы A= (aij) m,n и B= (bij) k,q называются равными, если они одинаковы по размеру (m=k, n=q) и их соответствующие элементы равны (aij = bij).
Сложение матриц. Складывать можно лишь матрицы одинакового размера. Суммой двух матриц A= (aij) m,n и B =(bij) m,n называется матрица C =(cij) m,n того же размера, причем элементы матрицы C равны сумме соответствующих элементов матриц A и B, т.е.
C = A+B, если cij = aij + bij. (1.10)
Пример. 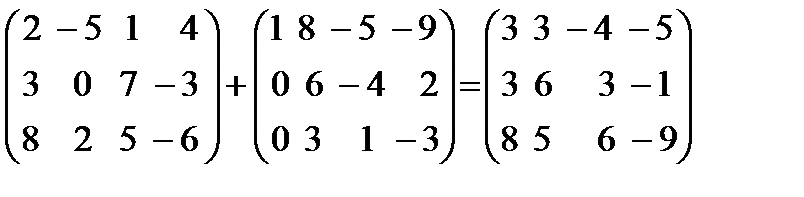 .
.
Умножение матрицы на число. Произведением матрицы A= (aik) m,n на число a называется матрица C =(cij) m,n, элементы которой получаются из соответствующих элементов матрицы A умножением на число a:
C = a A, где cij = a × aij. (1.11)
Пример.
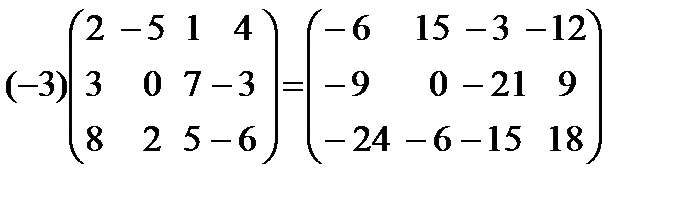 .
.
Произведение матриц. Произведение матриц A mk ∙B kn = Ckn определено только в том случае, если число столбцов матрицы A равно числу строк матрицы B, при этом матрица С имеет размер m∙ n. Элементы матрицы С определяются по формуле
 (1.12)
(1.12)
Умножение матриц производится по правилу "строка на столбец". Произведение матриц не перестановочно, в общем случае A∙B ≠ B∙A.
Пример. Найти произведения матриц A =  и B =
и B =  .
.
Поскольку это квадратные матрицы одного размера, то умножение таких матриц возможно, причем существует и АВ и ВА. В соответствии с (1.12) имеем:


Если A, B - квадратные матрицы одного порядка, то det (A ∙ B) = detA ∙ detB.
Транспонирование матриц. Рассмотрим произвольную матрицу
 .
.
Матрица  полученная из матрицы A заменой строк столбцами, называется транспонированной по отношению к A.
полученная из матрицы A заменой строк столбцами, называется транспонированной по отношению к A.
Например, если A = 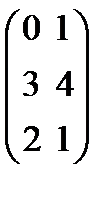 , то At =
, то At =  .
.






