Базис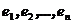 
называется каноническим для симметричной (эрмитовой) билинейной функции, если ее матрица в этом базисе диагональная.
Теорема 4.3 Лагранжа. Для любой эрмитовой функции существует канонический базис.
Доказательство проведём индукцией по рангу r матрицы эрмитовой формы F. Если r =0, то матрица нулевая, утверждение очевидно. Допустим, что теорема верна для r -1. Докажем ее истинность для r. Рассмотрим три случая
а) 
, тогда положим 
и 
, где k >1. В данном случае матрица перехода S будет отличаться от единичной матрицы только первой строкой, равной 
и S [ x ]=[ x ’], Q [ x ’]=[ x ], где 
. Матрица Q отличается от единичной матрицы только первой строкой, равной (1,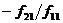 
,…, 
). После замены координат, получим матрицу билинейной формы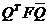 
, которая имеет следующий блочный вид 
. Поскольку ранг 
равен r -1, то по предположению индукции эрмитову матрицу можно привести к каноническому виду. Пусть 
. Тогда 
и теорема в этом случае доказана.
б)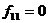 
и существует k, что 
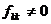переставим первый и k базисные вектора, и далее перейдем к пункту а).
в) 
для всех k и найдётся не нулевой элемент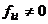 
, где 
. Возможны два случая:
-
тогда прибавим к k базисному вектору l базисный вектор и получим случай б) -
тогда прибавим к k базисному вектору l базисный вектор, умноженный на i, и получим случай б). Теорема доказана.
Базис эрмитовой билинейной функции f (x,y) называется нормальным, если матрица билинейной функции в этом базисе имеет диагональный вид, и ее главная диагональ равна (1,..,1,-1,..,-1,0..,0).
Для отыскания матрицы перехода можно поступать следующим образом. Припишем к матрице F единичную матрицу справа. Затем будем производить элементарные преобразования со строками расширенной матрицы и столбцами матрицы F. Причем, если к строке k прибавим строку j, умноженную на число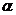 
, то затем к столбцу k прибавим столбец j, умноженный на число 
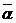. После приведения матрицы F к диагональному виду справа будет расположена матрица, все элементы которой комплексно сопряжены к матрице перехода.
Следствие 4.5 Для эрмитовой формы существует нормальный базис если поле R или C.
Доказательство. Построим канонический базис. Далее, если 
, то умножим j базисный вектор на число 
. Затем перестановкой базисных векторов приведем матрицу к нормальному виду.
Следствие 4.6 Если все угловые миноры матрицы F отличны от нуля, то существует верхняя треугольная матрица Q, которая приводит F к диагональному виду.
Доказательство проведем индукцией по рангу F. По теореме Лагранжа существует матрица Q, приводящая F к диагональному виду. Докажем, что она верхняя треугольная матрица. Обозначим через 
угловой минор j -го порядка матрицы F. Так как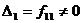 
, то выполняется пункт а) теоремы Лагранжа. Матрица перехода Q верхняя треугольная. Угловой минор матрицы порядка k -1, умноженный на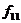 
, равен 
(угловому минору порядка k матрицы F). По предположению индукции, найдется
верхняя треугольная матрица Q’, приводящая матрицу к диагональному виду. Но тогда 
- верхняя треугольная матрица, а 
- диагональная матрица.
