Расстоянием между множествами X и Y называется 
.
Рассмотрим задачу нахождения расстояния от точки x до подпространства W. В начале рассмотрим случай, когда подпространство задано в виде линейной оболочки системы векторов.
Теорема 2.5. Расстояние от точки до подпространства достигается на перпендикуляре, опущенном из точки x на подпространство.
Доказательство. Представим 
. Расстояние от точки x до подпространства W равно 
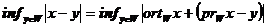. Векторы 
и 
ортогональны друг другу, и по неравенству Бесселя 
, причем равенство достигается только в случае 
. Тем самым установлено 
, что и требовалось.
Пусть 
и система векторов 
линейно независимая. Расстояние от точки x до подпространства W можно найти как отношение объема k +1-мерного параллелепипеда натянутого на векторы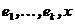 
к объему k -мерного параллелепипеда натянутого на векторы . Таким образом, справедлива формула 
. К сожалению, эта формула не позволяет находить проекцию и ортогональную составляющую вектора. Для нахождения проекции можно поступать следующим образом. Представим 
и 
, а затем умножим скалярно на векторы вектор x. Получим систему линейных уравнений 
. Коэффициенты при неизвестных образуют матрицу Грама, определитель которой не равен нулю. Следовательно, система имеет единственное решение. Решив эту систему, найдем проекцию вектора x, а затем и ортогональную составляющую.
Рассмотрим случай, когда линейное подпространство задано системой однородных линейных уравнений Ax =0. Для простоты проведения рассуждений будем считать, что строки матрицы A линейно независимы. В ортонормированном базисе, коэффициенты при неизвестных в уравнении являются координатами вектора из ортогонального дополнения (см. п.2.4). Таким образом, по системе линейных уравнений можно найти базис ортогонального дополнения к пространству W. Обозначим базис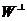 
через 
. Тогда представим 
и 
, а затем умножим скалярно на векторы вектор x. Получим систему линейных уравнений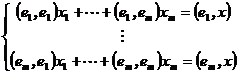 
. Коэффициенты при неизвестных образуют матрицу Грама, определитель которой не равен нулю. Следовательно, система имеет единственное решение. Решив эту систему, найдем ортогональную составляющую вектора x, а затем и проекцию.
Рассмотрим теперь задачу нахождения расстояния от точки x до линейного многообразия M. Эта задача легко сводится к аналогичной задаче построения расстояния от точки до подпространства. Действительно, пусть M = z + W, где z – произвольная точка из M, а W – подпространство. Тогда 
, то есть задача свелась к определению расстояния от точки x - z до подпространства W.
Линейное многообразие, заданное как множество решений одного линейного уравнения ax = b называется гиперплоскостью. Рассмотрим задачу отыскания расстояния от точки y до гиперплоскости ax = b. Перпендикуляр, опущенный из y на гиперплоскость равен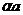 
и 
. Отсюда находим неизвестный параметр 
, а затем и расстояние 
.
Рассмотрим задачу определения расстояния между двумя линейными многообразиями 
и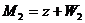 
. Расстояние между ними равно 
, то есть задача свелась к нахождению расстояния от точки y - z до подпространства 
. Заметим, что расстояние между линейными многообразиями достигается на общем перпендикуляре.
