Плоскость – линейное многообразие размерности 2. Плоскость в пространстве задаётся одним уравнением 
. Подпространство, соответствующее плоскости, задаётся однородным уравнением 
. В ортонормированном базисе левая часть уравнения является скалярным произведением вектора 
и вектора плоскости 
. Таким образом, множество векторов плоскости состоит только из тех векторов, которые ортогональны вектору нормали . Расстояние от точки до плоскости равно 
. Следовательно, коэффициент 
определяет удалённость плоскости от начала координат
Прямая в пространстве задаётся системой из двух уравнений (см. раздел Ошибка! Источник ссылки не найден.) 
, причём ранг матрицы, образованной коэффициентами при неизвестных, равен 2. Разберём геометрический смысл коэффициентов. Представив прямую как пересечение двух плоскостей, приходим к выводу, что векторы 
и 
образуют базис плоскости перпендикулярной исходной прямой.
Евклидово пространство. Скалярное произведение.
Пусть V линейное пространство над полем вещественных чисел. Функция 
, ставящая каждой паре векторов в соответствие число, называется скалярным произведением если выполнены аксиомы
1. Линейность по первому аргументу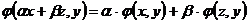 
.
2. Симметричность: 
3. Положительная определенность 
при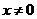 
.
Пространство над полем вещественных чисел, в котором введено скалярное произведение называется евклидовым.
Величина 
называется длиной вектора.
Пусть 
базис V. Выразим скалярное произведение векторов через координаты векторов. Координаты вектора x в базисе e обозначим через 
. Тогда 
. Пользуясь свойством линейности выводим 
. Используя симметричность скалярного произведения и линейности по первому аргументу выводим 
. Обозначим через G матрицу Грама базисных векторов, то есть матрицу на пересечении строки i столбца j стоит скалярное произведение i-го и j-го вектора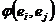 
. Используя матричные операции умножения получаем 
.
Изменение матрицы Грама при изменении базиса.
Допустим, в евклидовом пространстве V заданы два базиса и 
. Обозначим через 
матрицу перехода, связывающие координаты вектора в разных базисах. Пусть для определённости 
. Скалярное произведение не зависит от выбора базиса, поэтому 
. Подставим в правую часть равенства вместо координат вектора в базисе e их выражение через координаты в базисе f. В результате придём к равенству 
. Поскольку полученное равенство справедливо для любых векторов x и y, то выводим 
.
Ортогональность.
Определение 2.1. Векторы называются ортогональными, если их скалярное произведение равно 0.
Теорема 2.1 (Пифагора). Пусть векторы x и y ортогональны, тогда 
.
Доказательство. 
, т.к. 
в силу ортогональности.
Теорема 2.2 (неравенство Бесселя). Пусть векторы x и y ортогональны, тогда 
.
Доказательство. По теореме Пифагора . Поскольку 
, то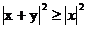 
, что и требовалось.
Теорема 2.3 (неравенство Коши-Буняковского-Шварца). 
.
Доказательство. Для любого a справедливо неравенство 
. Раскроем левую часть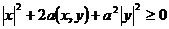 
. В левой части неравенства записан квадратный трехчлен. Выделим из него полный квадрат 
. Положив 
получим неравенство 
из которого вытекает 
. Извлекая квадратный корень, получаем требуемое.
Неравенство Коши-Буняковского-Шварца позволяет ввести угол между векторами, то есть косинус угла равен отношению 
.
Определение 2.2 Система векторов называется ортогональной, если каждая пара векторов из этой системе ортогональна.
Свойство 2.1. Ортогональная система векторов линейно не зависима.
Доказательство. Пусть 
- ортогональная система векторов и 
. Тогда 
. Таким образом 
и система векторов линейно независима.
Свойство 2.2. Матрица Грама ортогональной системы векторов – диагональная.
Процесс ортогонализации.
Пусть линейно не зависимая система векторов. Следующий процесс позволяет строить эквивалентную ей ортогональную систему векторов:
Положим 
, 
, …, 
…. Процесс не может быть продолжен только в случае, когда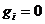 
. Но тогда 
, и, значит, 
, что противоречит линейной независимости исходной системы векторов.
Ортогональность построенной системы проверяется непосредственно. Допустим, ортогональность системы векторов 
установлена. Покажем, что вектор 
ортогонален всем векторам, построенным ранее него. Действительно, 
, где k =1,2,… i -1. В силу ортогональности системы векторов в сумме из правой части равенства только одно не нулевое слагаемое, получаемое при j = k. Следовательно, 
.
Следствие 2.1 В любом подпространстве конечномерного евклидова пространства имеется ортогональный базис.
Доказательство. Возьмем базис подпространства и применим к нему процесс ортогонализации. В результате будет построена ортогональная система векторов (а, значит, и линейно независимая) из этого подпространства. Поскольку количество векторов в построенной системе совпадает с размерностью подпространства, то, следовательно, построенная ортогональная система векторов является базисом подпространства.
Следствие 2.2. Любую ортогональную систему векторов можно дополнить до ортогонального базиса всего пространства.
Доказательство. Пусть - ортогональная система векторов. Дополним ее до базиса всего пространства векторами 
и к полученной системе применим процесс ортогонализации. В результате будет построен ортогональный базис 
всего пространства. Поскольку первые k векторов были ортогональны, то в процессе ортогонализации они не изменились, т.е. 
,…, 
. Таким образом, векторы 
дополняют ортогональную систему до ортогонального базиса всего пространства.
Следствие 2.3. Пусть - базис пространства, а - ортогональный базис пространства, полученный из базиса процессом ортогонализации. Тогда матрица перехода от одного базиса к другому является треугольной, и на ее главной диагонали стоят 1.
Доказательство. Согласно процессу ортогонализации имеем , 
, …, 
…, а, значит, матрица перехода P (ее столбцы – координаты базисных векторов) равна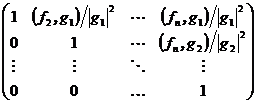 
.
