Однозначное отображение  линейного пространства V над числовым полем P в себя называется линейным преобразованием, если оно сохраняет линейность, то есть
линейного пространства V над числовым полем P в себя называется линейным преобразованием, если оно сохраняет линейность, то есть  для любых
для любых  и
и  .
.
Линейное преобразование полностью определяется своими значениями на базисных векторах. Действительно, пусть  базис V. Вектор x разложим по базису
базис V. Вектор x разложим по базису  , где
, где  - координаты вектора x. По свойству линейного преобразования имеем
- координаты вектора x. По свойству линейного преобразования имеем  . Перейдем в последнем равенстве от равенства векторов к равенству их координат
. Перейдем в последнем равенстве от равенства векторов к равенству их координат  , которое можно записать используя матричное умножение следующим образом
, которое можно записать используя матричное умножение следующим образом  . Матрица
. Матрица  называется матрицей линейного преобразования и обозначается
называется матрицей линейного преобразования и обозначается  . Матрица линейного преобразования связывает координаты образа с координатами исходного вектора
. Матрица линейного преобразования связывает координаты образа с координатами исходного вектора  .
.
Изменение матрицы линейного преобразования при изменении базиса.
Поскольку линейное преобразование частный случай линейного оператора, то можно воспользоваться полученной ранее формулой  , где P – матрица перехода. Матрицы A и B называются подобными, если существует невырожденная матрица P, что
, где P – матрица перехода. Матрицы A и B называются подобными, если существует невырожденная матрица P, что 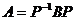 . Вопрос о подобии матриц сводится к решению системы линейных уравнений
. Вопрос о подобии матриц сводится к решению системы линейных уравнений  , где в роли неизвестных выступают элементы матрицы P, с дополнительным нелинейным условием
, где в роли неизвестных выступают элементы матрицы P, с дополнительным нелинейным условием  .
.
Алгебра линейных преобразований.
На множестве всех линейных преобразований пространства V расмотрим операции:
1. Умножение на число:  .
.
2. Сложение (вычитание) 
3. Умножение  .
.
Легко проверить линейность всех этих преобразований и вывести следующие формулы, связывающие их матрицы
1. 
2. 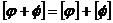
3. 
Линейное преобразование, переводящее каждый вектор в себя, называется тождественным преобразованием и обозначается 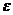 . В любом базисе матрица тождественного преобразования равна единичной.
. В любом базисе матрица тождественного преобразования равна единичной.
Пусть  - некоторый многочлен,
- некоторый многочлен,  - линейное преобразование пространства V. Сопоставим многочлену
- линейное преобразование пространства V. Сопоставим многочлену 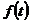 линейное преобразование
линейное преобразование  . Будем говорить, что преобразование
. Будем говорить, что преобразование 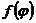 получено подстановкой
получено подстановкой  в многочлен
в многочлен 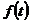 . Матрица
. Матрица 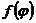 может быть вычислена по формуле
может быть вычислена по формуле  .
.
Свойство 7.1. Пусть 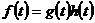 . Тогда
. Тогда  .
.
Инвариантные пространства
Подпространство W называется инвариантным относительно линейного преобразования  , если для любого x из W его образ
, если для любого x из W его образ  также принадлежит W.
также принадлежит W.
Свойство 7.2.  - инвариантное подпространство.
- инвариантное подпространство.
Доказательство. Пусть  . Тогда
. Тогда 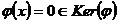 .
.
Свойство 7.3.  - инвариантное подпространство.
- инвариантное подпространство.
Доказательство. Пусть  , тогда
, тогда  .
.
Свойство 7.4. Пусть 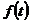 - многочлен, тогда
- многочлен, тогда  инвариантное пространство относительно
инвариантное пространство относительно  .
.
Доказательство. Пусть 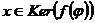 , то есть
, то есть 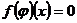 . Далее,
. Далее,  , то есть
, то есть  .
.
Свойство 7.5. Пусть 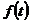 - многочлен, тогда
- многочлен, тогда  инвариантное пространство относительно
инвариантное пространство относительно  .
.
Доказательство. Пусть  , тогда
, тогда  . Далее,
. Далее, 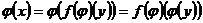 , то есть
, то есть  .
.
Знание инвариантных подпространств позволяет найти базис пространства, в котором матрица линейного преобразования имеет простую структуру. Действительно, пусть  базис инвариантного подпространства W. Дополним его до базиса всего пространства векторами
базис инвариантного подпространства W. Дополним его до базиса всего пространства векторами  . Координаты образов первых k векторов могут иметь только k первых ненулевых компонент. Следовательно, в матрице линейного преобразования содержится в левом нижнем углу блок размером (n - k)* k, состоящий из одних нулей.
. Координаты образов первых k векторов могут иметь только k первых ненулевых компонент. Следовательно, в матрице линейного преобразования содержится в левом нижнем углу блок размером (n - k)* k, состоящий из одних нулей.
Если пространство V представляется в виде прямой суммы инвариантных подпространств W и U, то построим базис пространства V, объединив базисы W и U. В построенном базисе матрица линейного преобразования будет иметь блочно диагональный вид.
Таким образом, структура матрицы линейного преобразования имеет тем более простой вид, чем меньше размерность инвариантных подпространств, в прямую сумму которых расщепляется исходное пространство V.




