Пусть 
базис W. Разложим вектор x из W по этому базису 
и найдем его образ 
. Из полученного равенства видно, что образ вектора определяется координатами вектора и значениями линейного оператора на базисных векторах. Обозначим через 
базис V. Координаты вектора x из W в базисе обозначим через 
, а координаты вектора y из V в базисе обозначим через 
. Перейдем в последнем равенстве от равенства векторов к равенству их координат 
, которое можно записать используя матричное умножение следующим образом 
. Матрица 
называется матрицей линейного оператора и обозначается 
.
Изменение матрицы линейного оператора при изменении базиса.
Получим формулу изменения матрицы линейного оператора при изменении базиса в пространствах V и W. Пусть 
новый базис W, а 
новый базис V. Координаты вектора в разных базисах связаны матрицей перехода. Пусть [ x ] e = T [ x ] h и [ y ] f = Q [ y ] g. Отсюда и равенства 
выводим 
или 
. Сопоставляя полученное равенство с 
, получаем равенство матриц 
.
Алгебра линейных операторов.
Обозначим через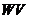 
множество линейных операторов, действующих из пространства W в пространство V. На множестве 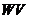определим операции умножения оператора на скаляр 
и сложение операторов 
. Оператор назовем нулевым, если все векторы переводятся в ноль. Нулевой оператор обозначим через 0, т.е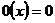 
. Относительно операций умножения на скаляр и сложения множество линейных операторов 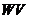образует линейное пространство. Отметим, что 
и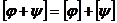 
.
Пусть W, V, U – линейные пространства над полем P, а 
линейный оператор из W в V, 
- линейный оператор из V в U. Отображение 
из W в U является линейным оператором и обозначается 
. Пусть 
- базис W, 
- базис V, 
- базис U, тогда 
.
Простейший вид матрицы линейного оператора.
Эквивалентность матриц
Матрицы A и B называются эквивалентными, если найдутся невырожденные матрицы Q и T, что A = QBT.
Теорема 6.1. Если матрицы эквивалентны, то их ранги равны.
Доказательство. Поскольку ранг произведения не превосходит ранги сомножителей, то 
. Так как 
, то 
. Объединяя два неравенства, получаем требуемое утверждение.
Теорема 6.2. Элементарными преобразованиями со строками и столбцами матрицу A можно привести к блочному виду 
, где 
- единичная матрица порядка k, а 0 – нулевая матрица соответствующих размеров.
Доказательство. Приведем алгоритм приведения матрицы A к указанному виду. Номера столбцов будут указываться в квадратных скобках, а номера строк – в круглых скобках.
1. Положим r =1.
2. Если 
то перейдем на шаг 4, иначе перейдем на шаг 3.
3. Сделаем преобразования со строками 
, где i = r +1,…, m, и со столбцами 
, где j = r +1,…, n, и 
. Увеличим r на 1 и вернемся на шаг 2.
4. Если 
, при i = r +1,…, m, j = r +1,…, n, то конец. В противном случае найдем i, j > r, что 
. Переставим строки 
и столбцы 
, вернемся на шаг 2.
Очевидно, что алгоритмом будет строиться последовательность эквивалентных матриц, последняя из которых имеет требуемый вид.
Теорема 6.3. Матрицы A и B одинаковых размеров эквивалентны тогда и только тогда, когда их ранги равны.
Доказательство. Если матрицы эквивалентны, то их ранги равны (Теорема 6.1). Пусть ранги матриц равны. Тогда найдутся невырожденные матрицы, что 
, где r = rgA = rgB (Теорема 6.2). Следовательно, 
, и матрицы A и B – эквивалентны.
Результаты данного пункта позволяют находить простейший вид матрицы линейного оператора и базисы пространств, в которых матрица линейного оператора имеет этот простейший вид.
