В Маткаде присутствует возможность применить к графику сглаживание, даже если он строился по малому количеству точек. Итог смотрите на рисунке ниже, а ход действий здесь.
Создаете две матрицы, обозначенные gx и gy, каждая с одним столбцом при помощи значка [::] с панели Matrix (для включения панели идите во View-Toolbars->Matrix). Это опорные точки, затем вводите переменную x с шагом 0.1, например. Это надо делать обязательно при помощи панели Matrix, не пытайтесь просто печатать две точки, выдаст ошибку.
Смысл m..n такой - [1-ое значение],[первое значение + шаг]..[последнее значение].
Далее нужно задать вспомогательную функцию - G:=lspline(gx,gy) (Внимание! Первая буква L маленькая, а не i!). Умные слова про эту функцию услышите на матмоде или почитайте в интернете. Итоговым шагом является график, где по оси Y вы вводите interp(G,gx,gy,x). Вот график и стал гладким. По аналогии можете теперь сгладить любой график, построенный по точкам в MathCad. 
Как построить график функции
Для того, чтобы построить график функции нужно задать функцию, например y(x):=x2. Вводить это нужно прямо с клавиатуры. На поле графика у оси 0y посередине пишете y(x), а по другой оси - x.
Задачи для самостоятельного решения
Построить графики функций в средах Mathcad и Excel.
а)у=х2 ,у=х2+1,у=(х-2)2
б)у=1/х, у=1/(x-2),y=1/x -2 на одной координатной плоскости.
Построить графики функций в средах Mathcad и Excel.
1.y=(x-2)2-1
2.y=1-√1-x
3.y=√x+4 -2
Построить графики функций в средах Mathcad и Excel.
y = sin (x - π/3).
y = cos x - 3
y = - sin x + 1,5
y = cos (x - 1) – 3
Список литературы
http://enmash.info/postroenie-grafikov-v-mathcad.html
http://excelpractic.ru/kak-postroit-grafik-v-excel.html
ПРАКТИЧЕСКАЯ РАБОТА № 6
«Решение содержательных задач из различных областей науки и практики».
Цели урока:
1) Обобщить теоретические знания по теме: подготовка к ЕГЭ по математике. Решение содержательных задач из различных областей науки и практики. Интерпретация, учёт реальных ограничений.
2) Рассмотреть алгоритмы решений заданий теме «подготовка к ЕГЭ по математике. Решение содержательных задач из различных областей науки и практики.», решить задачи.
3) Формировать умение ставить цели и реализовывать их.
Теоретический материал
Ход работы:
Используя теоретический материал, представленный ниж, выполните задания своего варианта.
Современный мир неожиданно обнаружил, что математика уверенно расположилась в самых разных его частях и уголках. Сейчас никого не удивишь словосочетаниями "математическая лингвистика", "математическая биология", "математическая экономика" и т.п. — какую дисциплину ни взять, вряд ли кому-нибудь покажется невозможным присоединение к ее наименованию эпитета "математический". Распространение математики вширь сопровождается се проникновением вглубь. Математика занимает сегодня видное место в жизни общества.
Сферу приложения математики мы можем увидеть из схемы:
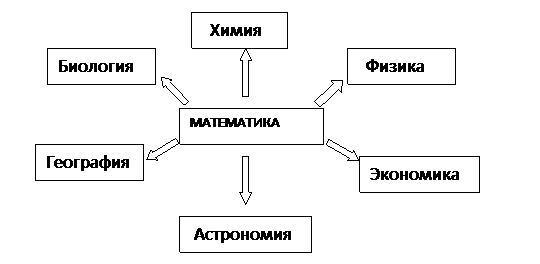
Математика и физика.
В физике широко распространена показательная функция:
- Барометрическая формула:
p = p 0 e – h / H
- Движение тела в сопротивляющейся среде:
V = v 0 e - kt / m
- Радиоактивный распад:
m (t)= C e – kt = m 0 2- t / T
- Охлаждение тел:
T = T 1 - C e - kt
Задача:
Два тела имеют одинаковую температуру 100о. Они вынесены на воздух (его температура 0о). Через 10 минут температура одного тела стала 80о, а второго 64о. Через сколько минут после начала остывания разность их температур будет равна 25о?
Решение:
Температуры первого и второго тел в момент времени R1=100е-k1t, R2=100e-k2t,
e-1Qk1 =8/10, e-1Q2=64/100, е-k1= (4/5)1/10, е-k2=(64/100)1/10.
Требуется найти момент времени t, когда R1(t)-R2(t)=25. Получаем уравнение:
100(е-k1t- е-k2t)=25, т.е. е-k1t- е-k2t=1/4.
(4/5)t/10 – (64/100)t/10=1/4;
(4/5)t/10 – (16/25)t/10=1/4;
(4/5)t/10 – (4/5)2t/10=1/4.
Пусть у =(4/5)t/10, тогда получаем уравнение:
-у2+ у – 1/4=0.
Решая это уравнение, получаем у=½, т.е (4/5)t/10=½. Логарифмируя по основанию 10, получим t/10 * lg 0,8 = lg ½, откуда t=10(-lg2)/3*lg2-1=31,06, т.е t=31,06.
Ответ: Через 31,06 минут.
2) Масса радиоактивного вещества уменьшается по закону m(t) = m02-t/T .В лаборатории получили вещество, содержащее в начальный момент времени m0 = 12 мг изотопа натрия-24, период полураспада которого равен Т = 15 ч. В течении скольких часов содержание натрия-24 в веществе будет превосходить 3 мг?
Решение:
Подставим в данную формулу известные данные, получим:
12*2-t/15>3
2-t/15>1/4
2-t/15>2-2
-t/15>-2
t<30
Ответ: В течение 30 часов.
Математика и химия.
Из задач по химии школьного курса изучения можно выделить задачи, при решении которых используются логарифмы:
- равновесные процессы;
- гидролиз растворов солей;
- скорость химической реакции изучает раздел кинетика;
- расчет рН.
Приведем примеры решения данных типов задач.
1) На сколько градусов надо повысить температуру для ускорения химической реакции в 59000 раз, если скорость реакции растет в геометрической прогрессии со знаменателем, равным 3 при повышении температуры на каждые 10о?
Решение:
3x=59000; lg 3x = lg 59000; x lg3 =lg 59000;
10° · x =10°·10° = 100°
Ответ: Надо повысить температуру на 100° для ускорения химической реакции.
2) Реакция при температуре 50°С протекает за 2 мин. 15 сек. За сколько времени закончится эта реакция при температуре 70°С, если в данном температурном интервале температурный коэффициент скорости реакции равен 3?
Решение. При увеличении t с 50° до 70° С скорость реакции в соответствии с правилом Ван-Гоффа возрастает:
= γ(t2 - t1)/10
Где t2 = 70° С, t1=50°C, а υt2 и υt1– скорости реакции при данных температура.
Получаем:
= 3(70-50)/10 = 32 = 9
т.е. скорость реакции увеличится в 9 раз.
В соответствии с определением, 
реакция обратно пропорциональна t реакции, следовательно
,
где τ – время реакции при температуре t1 и t2, следовательно τ t2 = τ t1 * υt1/ υt2
Учитывая, что τ t1= 135 сек., определяем t при 70°С: τ t2= 135 * 1/9 = 15 сек
Ответ: τ t2=15 сек.
Математика и биология.
В биологии так же широко используется показательная функция. Рост различных видов микроорганизмов и бактерий, дрожжей и ферментов подчиняются одному закону: N=N0ekt. По этому закону возрастает количество клеток гемоглобина в организме человека, который потерял много крови.
Рассмотрим такие задачи:
1) Численность популяции составляет 5 тыс. особей. За последнее время в силу разных причин (браконьерство, сокращение ареалов обитания) она ежегодно сокращалась на 8%. Через сколько лет (если не будут предприняты меры по спасению данного вида и сохранятся темпы его сокращения) численность животных достигнет предела – 2 тыс. особей, за которым начнётся вымирание этого вида?
Решение: Применим для вычисления времени формулу сложных процентов: 
где
2 тыс. – численность животных по истечению искомого времени;
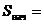5 тыс. – численность животных в начальный момент времени;
p = 8 - % сокращения численности животных.
Предварительно разделив обе части уравнения на 1000, получим:
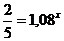
лет.
Ответ: Приблизительно через 11 лет.
2) Рассмотрим задачу об органическом росте в общем виде.
Пусть в начальный момент времени имелось q единиц некоторого компонента. В некоторый другой момент времени t имеющийся компонент изменился в p раз. Установите, через какой промежуток времени (начиная с начального момента) этот компонент достигнет заданного количества B единиц.
Решение: Для того чтобы это сделать, сначала напомним, что процессы, у которых происходит быстрый рост или быстрое затухание, описываются показательной функцией вида 
.
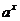В нашем случае будем считать, что начальный момент времени соответствует нулю, тогда 
, и значит, 
, т.е. функция, описывающая этот процесс, имеет вид 
. В следующий момент времени t у нас произошли изменения, описываемые уравнением 
, т.е. 
, откуда 
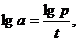
Таким образом, по данным условия мы получаем функцию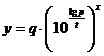 
. И теперь ясно, что мы ищем x, при котором 
, т.е. надо решить уравнение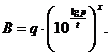 
Выполняя логарифмирование уравнения 
по основанию 10, получим 
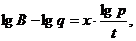
Ответ:
Математика и экономика.
1) Заглянем в кабинет экономиста одного из торговых предприятий. Перед которым возникла проблема – в каком соотношении закупить товары А и В. Можно закупить 8 единиц товара А и 5 единиц товара В. Торговое предприятие остановилось на первом варианте, т.к. при этом экономится сумма, достаточная для закупки 2-х единиц товара А. Какова цена товара А и товара В? Математика, выручай!
Пусть стоимость единиц товара А – х рублей, единиц товара В – у рублей. Тогда мы получим систему уравнений:
5х+8у=92;
8х+5у=92+2х;
Решив которую, получим, что стоимость одной единицы товара А-12 тысяч рублей, а цена одной единицы товара В-4 тысячи рублей.
2) Фирма состоит из двух отделений, суммарная величина прибыли, которых в минувшем году составила 13 млн. рублей. На этот год запланировано увеличение прибыли первого отделения на 75%, а второго - на 140%. В результате, суммарная прибыль фирмы должна вырасти в 2 раза. Какова величина прибыли каждого из отделений:
1)в минувшем году?
2)в текущем году?
Решение: Обозначим через х млн.рублей прибыль первого отдела и через у млн.рублей прибыль второго отдела в минувшем году. Тогда по условию задачи составим и решим систему уравнений с двумя переменными:
х+у=13;
1,75х+2,4у=26.
Решив которую, получим, что:
1)прибыль в минувшем году у первого отделения 8 млн.рублей, у второго-5 млн.рублей.
2)Прибыль в этом году у первого отделения 14 млн.рублей, у второго-12 млн.рублей.
3) А теперь заглянем в кабинет экономиста некоторой фирмы, которая производит детские велосипеды. Экономисты рассчитывают, сколько велосипедов в день надо производить по цене х рублей, чтобы прибыль была максимальной. И в этот раз нам не обойтись без математики…
Решение: Изначально надо установить зависимость между ценой х руб. одного велосипеда и количеством у единиц товара, приобретаемого за один день. Математическими методами было определено, что данная зависимость задана формулой у=570-3х. (1) Выясним, какую цену на товар установит фирма для того, чтобы прибыль от его реализации была наибольшей. Прибыль р находится по формуле р=ху. Согласно (1), р=х(570-3х), или р=-3х2+570х. Таким образом получается, что функция р=-3х2+570х является квадратичной. Функция будет достигать своего наибольшего значения при х=-570/(-3)*2=95.
Это наибольшее значение равно р=27075. Получается, что наибольшая выручка в 27075 рублей будет достигаться в том случае, если фирма реализует по цене 95 р. у=570-3*95=285 единиц товара.
