1. В данном кейсе нельзя писать решения!
За консультацией можно обращаться только к преподавателю или к эксперту-консультанту.
Внимательно рассмотрите решение задачи, представленной в справке.
Изучите, предложенную Вам, исследовательскую работу.
Следите за временем, отведенным на каждый этап работы.
Выполните поиск решения задачи,опираясь на сведения справочного материала,
Схема оформления мини-проекта в презентации
Слайд.
Тема_________________
Проблема_____________
Объект исследования________________
Слайд.
Цель, задачи________________
Слайд.
Рабочая гипотеза__________________
Слайды.
Результаты исследований_______________________
Слайды.
Сделайте вывод следующего содержания:
- что нового удалось узнать из сегодняшнего урока;
- что сделано за сегодняшний урок;
- что из этого является результатом, о котором можно написать в тексте своего отчета;
- что не понятно, какие проблемы возникли;
- какие есть идеи их решения, включая возможность изменения постановки всей задачи или её частей;
Слайд.
план работ на следующий период (например, две недели).
Вариант
Тема исследовательской работы «Спортивные ставки и теория вероятностей»

Ход работы
Справка
Формула полной вероятности
Формула Байеса
Формула условной вероятности
Разбор решения практической задачи по теме варианта
Выполнение теста
Самостоятельная работа
- Справка
1.1 Формула полной вероятности
Допустим, что проводится опыт, об условиях которого можно заранее сделать взаимо исключающие друг друга предположения (гипотезы):

Мы предполагаем, что имеет место либо гипотеза  , либо
, либо 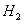 … либо
… либо  . Вероятности этих гипотез известны и равны:
. Вероятности этих гипотез известны и равны:

Тогда имеет место формула полной вероятности:

Вероятность наступления события А равна сумме произведений вероятности наступления А при каждой гипотезе на вероятность этой гипотезы.
1.2 Формула Байеса
Она позволяет пересчитывать вероятность гипотез в свете новой информации, которую дал результат А. Формула Байеса в известном смысле является обратной к формуле полной вероятности.

1.3 Условная вероятность
У словной вероятностью  (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

В частности, отсюда получаем:







