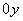Рассмотрим функцию с натуральным логарифмом  .
.
Выполним поточечный чертеж:

Если позабылось, что такое логарифм, отсылаю вас к школьным учебникам, академик Холмогоров свой хлеб все-таки не зря ест.

В заключение параграфа скажем еще об одном факте: Экспоненциальная функция  и логарифмическая функция
и логарифмическая функция  – это две взаимно обратные функции. Если присмотреться к графику логарифма, то можно увидеть, что это – та же самая экспонента, просто она расположена немного по-другому.
– это две взаимно обратные функции. Если присмотреться к графику логарифма, то можно увидеть, что это – та же самая экспонента, просто она расположена немного по-другому.
Графики тригонометрических функций
С чего начинаются тригонометрические мучения в школе? Правильно. С синуса
Построим график функции 

Данная линия называется синусоидой.
График косинуса
Построим график функции 

Графики тангенса и котангенса
Построим график функции 

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением  . Вот его график:
. Вот его график:

Графики обратных тригонометрических функций
Построим график арксинуса 

Построим график арккосинуса 

Построим график арктангенса 

Всего лишь перевернутая ветка тангенса.
Перечислим основные свойства функции  :
:

Свойства арккотангенса вы вполне сможете сформулировать самостоятельно. Отметим, что арккотангенс, как и арккосинус, не является четной или нечетной функцией.
При исследовании функции и изучении её свойств с целью построения графика находят: область определения функции D(f и, если возможно, область изменения E(f);
1) точки разрыва функции и промежутки непрерывности;
2) точки пересечения графика с осями координат;
3) промежутки знакопостоянства функции;
4) чётность, нечётность, периодичность;
5) критические точки функции, точки экстремума, экстремумы, промежутки монотонности;
6) промежутки выпуклости, вогнутости графика функции, точки перегиба;
7) асимптоты графика функции;
8) дополнительные точки (если это необходимо).
Строится график функции. Примеры.
| Способ построения графиков функций по точкам: | |

| Вытекает из определения графика функции. Он является длинным и недостаточно надежным. Применяется в школьном курсе математики при первоначальном знакомстве с простейшими функциями. (На графике функция  ). ).
|
Построение графиков функций на основании результатов исследования функции (без использования понятия производной)





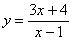


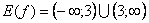
 и
и 
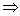 Ни четная, ни нечетная
Ни четная, ни нечетная
 и
и