Решение уравнений методом введения новой переменной.

Суть метода поясним на примере.

П р и м е р: Решить уравнение .

Р е ш е н и е. Положим , получим уравнение , откуда находим . Задача сводится к решению совокупности уравнений

Û

Первое квадратное уравнение не имеет действительных корней, так его дискриминант отрицателен. Из второго находим . Это корни заданного уравнения.

Биквадратным называется уравнение вида , где а ¹ 0. Биквадратное уравнение решается методом введения новой переменной: положив , придем к квадратному уравнению .

Иррациональные уравнения.

Иррациональным называется уравнение, в котором переменная содержится под знаком корня или под знаком возведения в дробную степень. Одним из методов решения таких уравнений является метод возведения обеих частей уравнения в одну и ту же степень:

А) преобразуем заданное иррациональное уравнение к виду:

;

Б) возводим обе части полученного уравнения в n - ую степень:

;

В) учитывая, что , получаем уравнение

f(x) = g(x);

Г) решаем уравнение и делаем проверку, так как возведение обеих частей уравнения в четную степень может привести к появлению посторонних корней. Эта проверка осуществляется с помощью подстановки найденных значений переменной в исходное уравнение.

Пример. Решить уравнение

Решение.

Возведем обе части уравнения в квадрат.
x² - 3 = 1;
Перенесем -3 из левой части уравнения в правую и выполним приведение подобных слагаемых.
x² = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.

Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение.
Проверка.
При x₁ = -2 - истинно:
При x₂ = -2 - истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.

Пример. Решить уравнение .

Это уравнение можно решить по такой же методике как и в первом примере, но мы поступим иначе.

Найдем ОДЗ данного уравнения. Из определения квадратного корня следует, что в данном уравнении одновременно должны выполнятся два условия:

а) x - 9 0;

x 9;

б) 1 - x 0;

-x -1;

x 1.

ОДЗ данного уранения: x .

Ответ: корней нет.

 

Виды неравенств

Пример:   Решить неравенство

Решение.

Частное двух чисел положительно в том случае, когда и делимое, и делитель положительны, или они отрицательны. Опираясь на это утверждение составим совокупность двух систем неравенств.

Сначала решим систему неравенств

Первая система равносильна неравенству х > 1.

Теперь, решаем систему неравенств:

Вторая система равносильна неравенству x < -1.

Ответ: x >1 и x < -1.

Пример:   Решить неравенство (1)..

Решение.  Вычтем из обеих частей неравенства функцию получим неравенство 3х > 9.

Разделим обе части полученного неравенства на положительное число 3 в результате получим x > 3 (2). Выполнив это преобразование, мы заменили неравенство (1) неравенством (2). Эти неравенства не равносильны.(1) (2).

M = (- ; 8) (8; + )- ОДЗ неравенства (1).

B = (3; + ) - это решение неравенства (2).

Найдем множество решений неравенства (1)

A = B M =((- ; 8) (8; + ) (3; + ) = (3; 8) (8; + ),

Ответ: x (3; 8) (8; + ).

Метод интервалов

Пример:  Решить неравенство.

Решение.

ОДЗ: откуда имеем x [-1; 5) (5; + )

Решим уравнение Числитель дроби равен 0 при x = -1, это и есть корень уравнения. Отметим найденный корень на чертеже (черным кружком, т.к. неравенство нестрогое), предварительно отметив ОДЗ:

Чтобы определить знак на промежутке (-1; 5) возьмем число 0, Чтобы определить знак на втором промежутке возьмем число 8,

Точки 0 и 8 выбирались произвольно, но так, чтобы упростить процесс вычисления каждого значения функции.

Ответ: (-5; + ).

Пример:    Решить неравенство

Решение.

Используя свойство частного и определение квадратного корня делаем вывод, что откуда ОДЗ: x (0; 1) (1; 7) (7; + )

Решим уравнение

x = 1.

На промежутке (0;1) возьмем точку 0,5;

На промежутке (1; 7) возьмем точку 4,

На промежутке (7; + ) возьмем точку 9,

Расставим знаки на координатной прямой.

Таким образом, решением данного неравенства является множество чисел принадлежащих промежутку (0; 1) (1; 7)

Пример:   Решить неравенство (2x - 6)(3x + 12)(5x + 1)<0.

Решение.

Нули функции: - 4; - 0,2; 3.

Функция в левой части неравенства представляет собой произведение не повторяющихся множителей, значит знаки этой функции чередуются cправа на лево с "+" на "-"....

Решение данного неравенства x (- ; -4) (-0,2; 3).

Пример:    Решить неравенство 7 - x.Введем вспогательную переменную. Пусть t = , где t 0, (из определения квадратного корня)
тогда t² = x + 5; откуда x = t² - 5 и имеем неравенство t 7 - t² + 5;

t² + t - 12 0;

ОДЗ: t R.

t² + t - 12 = 0;

t₁ = -4; t₂ = 3.

f(t) = t² + t - 12; эта функция непрерывна на всей области определения. Формулу, задающую функцию, удобнее записать так f(x) = (x - 3)(x + 4).

f(4) =4 ² + 4 - 12 = 8 >0;

Таким образом, функция f(t) = t² + t - 12 принимает значения небольшие 0, если -4 t 3. Так как t 0, то 0 t 4. Осуществим обратный переход к переменной x, тогда

0 3. Так как все части неравенства неотрицательны, то возведем их в квадрат 0 x + 5 9, откуда -5 x 4 и, следовательно,

x [-5; 3].

Ответ: x [-5; 3].

Пример:    Решить неравенство 2x² - 8x + 6 > .

Решение.

В левой части неравества вынесем 2 за скобки 3(x² - 4x + 3) > и введем вспомогательную переменную.

Пусть t = , тогда t > 0 и 2t² > t; 2t² - t > 0; t(2t -1) > 0.

В левой части неравенства задана квадратная функция, в которой старший коэффициент равен 1, а нули 0 и 0,5. Из свойств этой функции следует:

Таким образом неравенство 2t² > t равносильно неравенству t > 0,5.

Выполняем обратную замену переменных.

> 0,5, где x < 1 или x > 3.

x² - 4x + 3 > 0,25;

4x² - 16x + 11 > 0;

D/4 = 64 - 44 = 20, D > 0.

x₁ = , x₂ =

Нетрудно установить, что 0,5 < < 1 и 3 < < 3,5.

Таким образом решением исходного неравенства является следующее множество x (- ; ) (; + ).

Ответ: (- ; ) (; + ).

 

Пример:    Решить неравенство 2sin²x - 3sinx - 2 < 0.

Решение.

Пусть sinx = t, где t [-1; 1] (1), тогда получим квадратное неравенство
2t² - 3t - 2 < 0.

Для его решения будем использовать свойства квадратной функции.

1) Её старший коэффициент равен 2.

2) D = 3² - 4 2(-2) = 9 + 16 = 25, следовательно, D > 0.

3) t₁ = -0,5; t₂ = 2, поэтому решением неравенства является множество чисел
t (- ; - 0,5) (2; + ) (2).

Пересечение множеств (1) и (2) есть множество [-1; -0,5).

Произведем обратный переход к переменной х, получим неравенство.

-1 sinx < -0,5. Для решения этого двойного неравенства воспользуемся свойствами функции y = sinx.

<="" p="">

x (- + 2 k; - + 2 k), где k Z.

Ответ: x (- + 2 k; - + 2 k), где k Z.

Пример:    Решить неравенство 3 > lg() + 2.

Решение.

Так как -х > 0 при x < 0 и = |x|, где |x| = -x при указанных выще условиях, то заданное неравенство, при x < 0, можно заменить равносильным ему неравенством 3 > lg(-x) + 2. Пусть t = , получим квадратное неравенство t² - 3t + 4 < 0.

1) Старший коээфициент квадратного трехчлена положителен.

2) Корни квадратного трехчлена: t₁ = 1, t₂ = 2.

3) Квадратный тречлен принимает отрицательные значения при 1 < t < 2.

Получаем неравенство 1 < < 2. Все три части неравенства положительны, возведем их в квадрат.

1 < lg(-x) < 4;

-1000 < x < -10.

Ответ: (-10000; -10).

Упражнения для самостоятельной работы.

        3х + (20 – х) = 35,2,

        ,

    (х – 3) - х = 7 – 5х.

(х + 2)  - 11(х + 2) = 12.

   х  = х ,

  3у  = 96,

   х  + х  + х + 1 = 0,

   – 5,5n(n – 1)(n + 2,5)(n - ) =0.

         а)2 + =4,

      =-5,

      = - x. а) =

      2а х – 5 = 17.

х  + 2х - 15=0;

 (х - 4х) - 7(х - 4х) +12=0;

х +9х - х -9=0;

у -15 =0;

х - 625=0.

Список литературы

1.Пехлецкий И. Д. Математика, СПО. - М.: Академия, 2013.

2.Григорьев С.Г., Задулина С.В. Математика, СПО. - М.: Академия, 2014.

3.Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика, СПО. - М.: Академия, 2014.

4.Валуце И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 2014.

5.Подольский В. А., Суходский А.М. Сборник задач по высшей математике. - М.: Высшая школа, 194.

6.Башмаков М.И. Математика, 10 кл. - М.: Академия, 2013.

7.Башмаков М.И. Математика, 11 кл. - М.: Академия, 2013.

 

ПРАКТИЧЕСКАЯ РАБОТА № 8

 «Производная»

Цели урока:

1) Обобщить теоретические знания по теме: «Производная».

2) Рассмотреть алгоритмы решений заданий теме «Производная», решить задачи самостоятельной работы с использованием геометрического и механического смысла производной.

3) Формировать ответственность; самоконтроль, рассудительность.

Теоретический материал

Ход работы:

Используя определения теории дифференциалов, представленные ниже выполните задания своего варианта.

1.Производнойфункции  в данной точке  называют предел отношения приращения функции ∆y к соответствующему приращению аргумента ∆x при условии, что ∆x→0, т.е.

2 Геометрическая интерпретация производной,, состоит в следующем: значение производной функции  в точке x равно угловому коэффициенту касательной, проведённой к графику функции в той же точке x,т.е.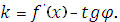

Уравнение касательной, как всякой прямой, проходящей через данную точку в данном направлении, имеет вид  – текущие координаты. Но  и уравнение касательной запишется так: . Уравнение нормали запишется в виде .

3. Механическое истолкование производной заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е.

Вариант № 1 1.Напишите уравнение касательной, проведенной к графику функции у = х ² + 2 x через точку с абсциссой х = 3. 2.Тело движется по прямой и при этом его координата меняется в зависимости от времени по закону х = 3 t 4 + 5 t + 6 (м). Найдите скорость тела и его ускорение в момент t = 7с. 3.Составьте и решите неравенство > 0, если =

Вариант №2 1.К графику функции y = f (x) = x ² + 6 x +7 проведена касательная через точку с абсциссой х = -1. Найдите угловой коэффициент касательной. 2.Тело движется по прямой и при этом его координата меняется в зависимости от времени по закону х = 2 t 3 + 3 t 2 + 4 (м). Найдите скорость тела и его ускорение в момент t = 2с. 3. Составьте и решите неравенство > 0, если =

Вариант №3 1.Маховик вращается и точки его поверхности движутся по закону j (t) = t + 6 t ² + 1 2 t (рад). Найдите угловую скорость и угловое ускорение точек в момент t = 1с. 2.К графику функции y = f (x) = 3 x 4 + 8 x +9 проведена касательная через точку с абсциссой х = -1. Найдите угловой коэффициент касательной. 3. Составьте и решите неравенство > 0, если =

 

Список литературы

1.Пехлецкий И. Д. Математика, СПО. - М.: Академия, 2013.

2.Григорьев С.Г., Задулина С.В. Математика, СПО. - М.: Академия, 2014.

3.Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика, СПО. - М.: Академия, 2014.

4.Валуце И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 2014.

5.Подольский В. А., Суходский А.М. Сборник задач по высшей математике. - М.: Высшая школа, 194.

6.Башмаков М.И. Математика, 10 кл. - М.: Академия, 2013.

7.Башмаков М.И. Математика, 11 кл. - М.: Академия, 2013.

 

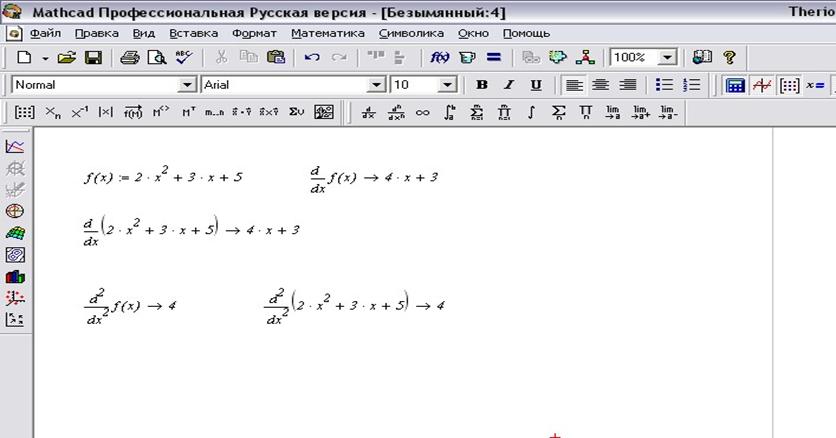
ПРАКТИЧЕСКАЯ РАБОТА № 9

 «Нахождение производных в среде Mathcad»

Цели урока:

1) Обобщить теоретические знания по теме: «Нахождение производных функций в среде Mathcad».

2) Рассмотреть алгоритмы решений заданий по данной теме, используя формулы вероятности событий, решить задачи.

3) Формировать умение  планировать свою деятельность, умение ставить цели и реализовывать их.

Теоретический материал