| Теория | Практика |
Задачи на движение. При решении задач на движение используется одна из трех формул:
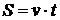 , , 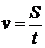 , ,  . Необходимо помнить, что величины должны быть в одной системе единиц, что большую помощь может оказать рисунок, график, таблица.
Задачи на движение по реке. При решении задач на движение по реке необходимо учесть, что . Необходимо помнить, что величины должны быть в одной системе единиц, что большую помощь может оказать рисунок, график, таблица.
Задачи на движение по реке. При решении задач на движение по реке необходимо учесть, что
 , ,  где: где:
 – скорость по течению реки; – скорость по течению реки;
 – скорость объекта при движении против течения реки; – скорость объекта при движении против течения реки;
 – собственная скорость движущегося объекта; – собственная скорость движущегося объекта;
 – скорость течения реки.
Решать их желательно, используя схемы или таблицы.
Задачи на бассейны и трубы. Такие задачи фактически являются задачами на движение. Работа или объем бассейна есть, условно говоря, путь, пройденный точкой; производительность, с которой выполняется работа или наполняется бассейн есть скорость.
Решение сложных задач целесообразно начать с повторения алгоритма решения системы уравнений с 2-мя неизвестными:
-Обозначить неизвестную величину переменной (при решении задачи с помощью системы уравнения вводят несколько переменных);
-Выразить через нее другие величины;
-Составить уравнение (или систему уравнений), показывающее зависимость неизвестной величины от других величин;
-Решить уравнение (или систему уравнений);
-Сделать проверку при необходимости;
-Выбрать из решений (или систему уравнений) те которые подходят по смыслу задачи;
-Оформить ответ.
Полезно вспомнить:
Задачи на проценты. Основным понятием является часть числа, если задана величина – скорость течения реки.
Решать их желательно, используя схемы или таблицы.
Задачи на бассейны и трубы. Такие задачи фактически являются задачами на движение. Работа или объем бассейна есть, условно говоря, путь, пройденный точкой; производительность, с которой выполняется работа или наполняется бассейн есть скорость.
Решение сложных задач целесообразно начать с повторения алгоритма решения системы уравнений с 2-мя неизвестными:
-Обозначить неизвестную величину переменной (при решении задачи с помощью системы уравнения вводят несколько переменных);
-Выразить через нее другие величины;
-Составить уравнение (или систему уравнений), показывающее зависимость неизвестной величины от других величин;
-Решить уравнение (или систему уравнений);
-Сделать проверку при необходимости;
-Выбрать из решений (или систему уравнений) те которые подходят по смыслу задачи;
-Оформить ответ.
Полезно вспомнить:
Задачи на проценты. Основным понятием является часть числа, если задана величина  , то ее , то ее  -я часть равна -я часть равна  , и определение: Процентом называется одна сотая часть величины , и определение: Процентом называется одна сотая часть величины  , то есть 1% = 1/100 от целого. Значит, целое составляет 100%.
Например: , то есть 1% = 1/100 от целого. Значит, целое составляет 100%.
Например:  ; ; 
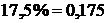 Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.Например, 125% = 125:100 = 1,25%
Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.Например, 125% = 125:100 = 1,25%
| 1. Из сосуда, доверху наполненного 88%-м раствором кислоты, отлили 2,5 литра жидкости и долили 2,5 литра 60%-го раствора этой же кислоты. После этого в сосуде получился 80%-й раствор кислоты. Найдите вместимость сосуда в литрах.
Решение.
Пусть х (литров) – вместимость сосуда.
1) Т.к. сосуд был доверху наполнен 88%-м раствором кислоты, то кислоты в нем было 0,88 х литров, а воды – 0,12 х.
2) В 2,5 литрах жидкости содержится 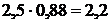 литра кислоты и 0,3 литра воды.
3) В 2,5 литрах 60%-го раствора этой же кислоты будет литра кислоты и 0,3 литра воды.
3) В 2,5 литрах 60%-го раствора этой же кислоты будет  литра кислоты и 1 литр воды.
4)Когда из первоначального сосуда отлили 2,5 л жидкости и долили 2,5 литров 60% раствора кислоты, то получилось литра кислоты и 1 литр воды.
4)Когда из первоначального сосуда отлили 2,5 л жидкости и долили 2,5 литров 60% раствора кислоты, то получилось  литров кислоты и литров кислоты и 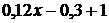 воды.
5) Т.к. в результате получается 80%-й раствор кислоты, то в нем будет 80% кислоты и 20% воды, т.е. выполняется условие воды.
5) Т.к. в результате получается 80%-й раствор кислоты, то в нем будет 80% кислоты и 20% воды, т.е. выполняется условие  . Решая это уравнение, получим . Решая это уравнение, получим 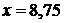 литров – вместимость сосуда.
Ответ: 8,75.
2. Расстояние между городами А и В равно 900 км. Два поезда одновременно отправляются, один из А в В, другой из В в А. Они встречаются в пункте С. Первый поезд прибывает в город В через 4 часа после встречи со вторым поездом, в второй прибывает в город А через 16 часов после встречи с первым поездом. Определите расстояние АС.
Решение. литров – вместимость сосуда.
Ответ: 8,75.
2. Расстояние между городами А и В равно 900 км. Два поезда одновременно отправляются, один из А в В, другой из В в А. Они встречаются в пункте С. Первый поезд прибывает в город В через 4 часа после встречи со вторым поездом, в второй прибывает в город А через 16 часов после встречи с первым поездом. Определите расстояние АС.
Решение.
 Расстояние от А до С в 2 раза больше расстояния от С до В. Добавим участок от А до Д, тогда tАД =4 (часа). АВ поделим на 3 равных участка. 900:3=300 км, т.е. AД=ДC=CB=300км. Итак, АС=AД+ДC=600 км.
Ответ: 600.
3. Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35%, а во втором — 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?
Решение. Пусть х — масса первого сплава, y — масса второго сплава. Тогда количество золота в первом сплаве составляет 0,3 х, а во втором — 0,55 у. Масса нового сплава равна
Расстояние от А до С в 2 раза больше расстояния от С до В. Добавим участок от А до Д, тогда tАД =4 (часа). АВ поделим на 3 равных участка. 900:3=300 км, т.е. AД=ДC=CB=300км. Итак, АС=AД+ДC=600 км.
Ответ: 600.
3. Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35%, а во втором — 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?
Решение. Пусть х — масса первого сплава, y — масса второго сплава. Тогда количество золота в первом сплаве составляет 0,3 х, а во втором — 0,55 у. Масса нового сплава равна  , а количество золота в нем составляет , а количество золота в нем составляет  . Получим уравнение . Получим уравнение  . Преобразуем уравнение, получим: . Преобразуем уравнение, получим:  , ,
 , , 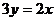 . Отсюда: . Отсюда:  .
Ответ: в отношении 3:2. Ответ может быть дан и в другом виде, например .
Ответ: в отношении 3:2. Ответ может быть дан и в другом виде, например  .
4. И пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?
Решение. Пусть скорость течения реки (и плота) х км/ч. Тогда скорость катера против течения равна .
4. И пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?
Решение. Пусть скорость течения реки (и плота) х км/ч. Тогда скорость катера против течения равна 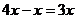 км/ч, а по течению км/ч, а по течению  км/ч. Следовательно, скорость катера против течения в 3 раза больше скорости плота, а по течению - в 5 раз больше скорости плота. Если плот до встречи проплыл км/ч. Следовательно, скорость катера против течения в 3 раза больше скорости плота, а по течению - в 5 раз больше скорости плота. Если плот до встречи проплыл  км, то катер — в 3 раза больше, т.е. км, то катер — в 3 раза больше, т.е.  км. После встречи катер пройдет км. После встречи катер пройдет  км, а плот - 5 раз меньше, т.е. км, а плот - 5 раз меньше, т.е.  км. Всего плот пройдет км. Всего плот пройдет 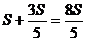 . Отношение пройденного плотом пути ко всему пути равно . Отношение пройденного плотом пути ко всему пути равно  .
Другое возможное решение. Пусть скорость течения реки (и плота) х км/ч. Тогда скорость катера против течения равна .
Другое возможное решение. Пусть скорость течения реки (и плота) х км/ч. Тогда скорость катера против течения равна 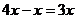 км/ч, а по течению км/ч, а по течению 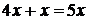 км/ч. Скорость сближения катера и плота равна км/ч. Скорость сближения катера и плота равна  км/ч. Встреча произошла через км/ч. Встреча произошла через  ч. За это время плот проплыл ч. За это время плот проплыл  км, а катер - км, а катер -  км. Обратный путь катер пройдет за км. Обратный путь катер пройдет за  ч. Плот за это время проплывет расстояние равное ч. Плот за это время проплывет расстояние равное  км, а всего он проплывет км, а всего он проплывет  км.
Ответ: плот пройдет км.
Ответ: плот пройдет 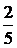 всего пути. всего пути.
|
| Модель 1 Баллы | Критерии оценки выполнения задания |
| 6 | Ход решения верный, все его шаги выполнены, получен верный ответ. |
| 5 | Ход решения верный, все его шаги выполнены, но допущена одна ошибка – в преобразованиях или в вычислениях, с ее учетом дальнейшие шаги выполнены правильно. |
| 0 | Другие случаи, не соответствующие указанным критериям. |
| Модель 2 Баллы | Критерии оценки выполнения задания |
| 4 | Ход решения верный, все его шаги выполнены правильно, получен верный ответ. |
| 3 | Ход решения верный, все его шаги выполнены, но допущена вычислительная ошибка или описка. |
| 2 | Найдены части пути, которые проплывет плот до и после встречи, но решение не доведено до конца и не найдена часть всего пути от А до В, пройденная плотом. |
| 1 | Найдены части пути, которые проплывет плот до и после встречи, но решение не доведено до конца и допущена одна арифметическая ошибка. |
| 0 | Другие случаи, не соответствующие указанным критериям. |
Реши сам:
1. Из пункта А в пункт В, расположенный выше по течению реки, вышла моторная лодка, собственная скорость которой в 5 раз больше скорости течения. Одновременно навстречу ей из пункта В отправился плот. Встретив плот, лодка сразу повернула назад и пошла вниз по течению реки. Какую часть пути от В до А пройдет плот к моменту возвращения лодки в пункт А?
2. Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышла лодка, собственная скорость которой в 2 раза больше скорости течения. Встретив плот, лодка сразу повернула назад и пошла вниз по течению. Какую часть пути от А до В останется пройти плоту к моменту возвращения лодки в пункт В?
3. При смешивании первого раствора соли, концентрация которого 40%, и второго раствора этой же соли, концентрация которого 48%, получился раствор с концентрацией 42%. В каком соотношении были взяты первый и второй растворы?
4 Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй — 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
5. На пост мэра города претендовало три кандидата: Андреев, Борисов, Васильев. Во время выборов за Васильева было отдано в 1,5 раза больше голосов, чем за Андреева, а за Борисова — в 4 раза больше, чем за Андреева и Васильева вместе. Сколько процентов избирателей проголосовало за победителя?
6. Рыболов отправляется на лодке от пристани против течения реки с намерением вернуться назад через 5 ч. Перед возвращением он хочет побыть на берегу 2 ч. На какое наибольшее расстояние он может отплыть, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
7. Моторная лодка отправилась по реке от одной пристани до другой и через 2,5 ч вернулась обратно, затратив на стоянку 15 мин. Найдите скорость течения реки, если собственная скорость лодки равна 18 км/ч, а расстояние между пристанями 20 км.
8. Расстояние между двумя пристанями по реке равно 21 км. Моторная лодка отправилась от одной пристани до другой и через 4 ч вернулась назад, затратив на стоянку 24 мин. Найдите собственную скорость моторной лодки, если скорость течения реки равна 2 км/ч.
9. Лодка может проплыть 15 км по течению реки и еще 6 км против течения за то же время, за какое плот может проплыть 5 км по этой реке. Найдите скорость течения реки, если известно, что собственная скорость лодки 8 км/ч,
10. Катер проплывает 20 км против течения реки и еще 24 км по течению за то же время, за какое плот может проплыть по этой реке 9 км. Скорость катера в стоячей воде равна 15 км/ч. Найдите скорость течения реки.
11. Клиент внес 3000 р. на два вклада, один из которых дает годовой доход, равный 8%, а другой — 10%. Через год на двух счетах у него было 3260 р. Какую сумму клиент внес на каждый вклад?
Вернуться в содержание






